Bevarande av den linjära momentia -principen, exempel, övningar.

De bevarande av linjär momentum av en kropp konstaterar att produkten från dess massa med dess hastighetsvektor är en konstant mängd, när kroppen är fri från interaktion med andra kroppar och med hastigheten uppmätt med avseende på ett fast eller icke-akut referenssystem.

När det finns flera kroppar som bara interagerar mellan dem, men inte med den yttre miljön, då linjär momentum av uppsättningen förblir också konstant över tid.

En astronaut i rymden är fri från all interaktion, därför dess linjära ögonblick

Det linjära ögonblicket, mängden linjär rörelse eller helt enkelt Momentum, Det betecknas med brevet p Och det är en vektorbelopp:

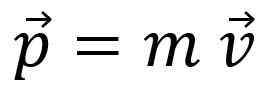
Det linjära ögonblicket är inte detsamma som hastigheten, även om förhållandet är uppenbart: till exempel har en lastbil som går till 20 km/h mer linjär tid än en cykel som rör sig med samma hastighet.

För att det linjära ögonblicket för en kropp ska förändras är det nödvändigt att en nettokraft verkar på den, annars förblir den konstant. Dessutom det linjära ögonblicket P av ett system som bildas av N-kropp Det är vektor summan av enskilda stunder:

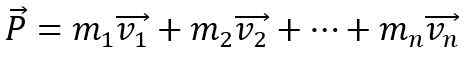
[TOC]

Princip för bevarande av mängden linjär rörelse

I en kropp fri från krafter (eller en där alla krafter på den avbryts) händer det att det linjära ögonblicket.

På samma sätt passerar det i ett system som bildas av flera kroppar som bara interagerar med varandra, men inte med den yttre miljön: systemets totala linjära ögonblick förblir fixat under uppsättningen av uppsättningen.

Denna bevarandeprincip anges så här:

Det totala linjära ögonblicket för en uppsättning n-kropp som bara interagerar med varandra, men inte med den yttre miljön, är en oundviklig mängd i tid.

Och matematiskt uttrycks det enligt följande:

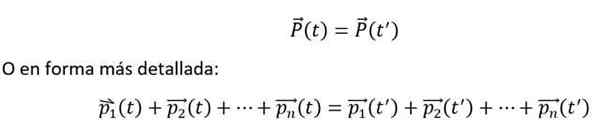
Den tidigare jämlikheten är uppfyllda, om och bara om n-Kroppar interagerar med varandra, men inte med den yttre miljön. Dessutom bör enskilda stunder alltid mätas med avseende på ett tröghetsreferenssystem.

Exempel

Exempel 1

Två astronauter i rymden är hämtade från händerna och förblir i en fast position med avseende på fartyget. Men de skjuter varandra, de börjar separera i motsatta riktningar, när de ses från fartyget.

Det kan tjäna dig: Theory of the Big Bang: Egenskaper, stadier, bevis, problem

I det här fallet, som samspelet mellan astronauter bara är bland dem genom deras händer, det totala linjära ögonblicket. Det vill säga total linjär tid 0.

Det linjära ögonblicket för varje astronaut förändrades dock. Ursprungligen hade var och en ett linjärt ögonblick 0 med avseende på fartyget, men efter att ha tryckt en kommer ut i en riktning och den andra i motsatt riktning, med icke-noll linjära stunder av lika stor storlek och motsatta adresser.

Således, när de enskilda ögonblicken läggs till vektor, erhålls den ursprungliga totala linjära momentumet som ett resultat, vilket är ogiltigt.

Å andra sidan bevarande av det linjära momentet. Men resultatet av att multiplicera dess massa med dess hastighet är lika med den produkt som erhålls genom att multiplicera massan på den andra med hastigheten på den andra.

Exempel 2

En valp finns på en flytande plattform i en sjö med lugnt vatten och dess ägare ser det från en brygga. I början är både plattformen och valpen i vila, men när valpen vill närma sig ägaren rör sig plattformen bort från bryggan.

Förklaringen till denna observation är just i principen om bevarande av den linjära momentumbeloppet. Systemet består av valpen och plattformen.

Valpen kan gå på plattformen tack vare friktionskraften mellan benen och ytan, i detta fall är friktionskraften en intern interaktionskraft mellan den och plattformen.

Uppsättningen är ett isolerat system, och plattformen kan röra sig horisontellt på sjön, fri från allt rörelsemotstånd. Å andra sidan, i vertikal riktning är alla krafter balans och kompenseras, och uppsättningen har ingen rörelse i den riktningen.

I denna situation uppfylls därför alla hypoteser så att principen om bevarande av det linjära momentumet tillämpas.

Exempel 3

En eskimo fångas i mitten av en glass, isen är så smidig att oavsett hur mycket försökt, Eskimo glider och alltid förblir på samma plats.

Det enda möjliga sättet att Eskimo lämnar sjön, är att den ligger i den riktning som ett tungt föremål som bär i ryggsäcken (förutsatt att en).

Kan tjäna dig: Geometrisk optik: Vilka studier, lagar, applikationer, övningar

Ansökningar

Skepp i rymden

Bevarande av det linjära ögonblicket. I detta fall uppnås fartygets impuls genom utvisning av gaser med hög hastighet, så att raketen kan röra sig i motsatt riktning som de förvisades.

Om fartyget ursprungligen är i vila, när bränslet bränns och utvisas, inträffar utvisningskraften mot själva fartyget. Det är en inre kraft mellan gaser och fartyget. Det finns inga yttre krafter och tillämpar därför bevarande av det linjära ögonblicket.

Eftersom det linjära momentet för gaser är detsamma och i motsats till fartyget, lyckas det lämna vila och genom att fortsätta att utvisa gaser ökar dess rörelse och därför dess hastighet.

Dagligt liv

Ett annat fall för bevarande av det linjära ögonblicket.

Det kan hävdas att principen i detta fall inte gäller, eftersom det finns en yttre kraft: motståndet som träet erbjuder mot kryddnejlika.

Vid tidpunkten för kontakt är emellertid kraften som hammaren skriver ut till nageln en inre kraft (mellan systemet som är nageln och hammaren) mycket större än motståndet som träet motsätter sig, och därför är det senare försumbar.

Hela linjära ögonblicket för hammaren, som är ganska stor på grund av dess stora massa och hastighet, överförs till nageln strax efter kollisionen. Observera att hela ögonblicket överförs, men inte all hammarens kinetiska energi, eftersom en del av den förvandlas till termisk energi till nageln och hammaren, som höjer temperaturen efter påverkan.

Övningar

Övning 1

Andrew och Berenice astronauter är utanför rymdstationen tagna från båda händerna och i vila med avseende på stationen. De kör skjuter händerna mot de andra och de släpps. Om Andrew, 70 kg massa rör sig vid 1 m/s med avseende på stationen, vad är Berenices hastighet med 49 kg massan?

Lösning

I detta fall tillämpas hypotesen om bevarande av den linjära momentumet tydligt, eftersom det inte finns några yttre krafter i yttre utrymme. Kraften som händerna driver båda astronauterna är en inre kraft.

Det kan tjäna dig: vågdiffraktion: koncept och exempel

Anta att Andrews massa är m_till och den av Berenice m_b. På samma sätt är hastigheterna på båda efter impulsen V_till För Andrew och V_b För berenice. Sedan appliceras bevarande av det linjära momentumet enligt följande:

M_till∙0 + M_b∙0 = M_till∙V_till+ M_b∙V_b

Rensa Berenices hastighet du har:

V_b = - (m_till / M_b) ∙ V_till

Placera numeriska värden:

V_b = - (70 /49) ∙ (1 m / s) eller = -1,43 m/s eller

Det vill säga att Berenice rör sig snabbt 1,43 m/s i motsatt riktning av Andrew.

Övning 2

En valp går mot sin ägare ovanpå en halvsiktad plattform. Källa: f. Zapata.

En 5 kg deg är i vila på en 15 kg plattform som flyter, också i vila, på en stillbild. Om valpen börjar gå på plattformen med en hastighet av 0,5 m/s med avseende på detta. Hur snabbt kommer valpen och plattformen angående en fast observatör att markera?

Lösning

Det kommer att tas som ett tröghetsreferenssystem till bryggan där valpägaren är. Ursprungligen är både valpen och den flytande plattformen i vila med avseende på bryggan.

När valpen beslutar att gå mot ägaren snabbt V ' När det gäller plattformen rör sig plattformen bort från våren med hastighet +V. Valpens hastighet med avseende på bryggan uppnås med vektor summan av dess hastighet med avseende på plattformen plus plattformens hastighet och betecknar den med:

v = -v' + V

Eftersom vattenmotståndet mot plattformens rörelse praktiskt taget är noll på grund av dess låga hastighet, kan det bekräftas att systemet som består av Valpen + plattformen Det är ett isolerat system och principen om bevarande av den linjära momentumet tillämpas:

0 = M ∙ V + M ∙ V

Kom ihåg att v = v ' + v du har:

0 = -M ∙ V ' + M ∙ V + M ∙ V

Det är: m ∙ v '= (m+m) ∙ v

Därför v = [m/(m + m)] v 'y v = - (m/m) v = - [m/(m + m)] v'

Att ersätta numeriska värden är:

V = [5/(5 +15)] ∙ 0,5 m/s = 0,125 m/s

Detta är den hastighet som vårplattformen rör sig bort.

V = -(15/20) ∙ 0,5 m/s = -0,375 m/s

Och detta är den hastighet som valpen närmar sig bryggan.

Referenser

1. Hertig universitet. Partiklar. Återhämtat sig från: Webhome.Phy.hertig.Edu.
2. Rex, a. 2011. Fysikens grunder. Pearson.
3. Sears, Zemansky. 2016. Universitetsfysik med modern fysik. 14th. Ed. Volym 1. Pearson.
4. Serway, R., Jewett, J. (2008). Fysik för vetenskap och teknik. Volym 1. 7th. Ed. Cengage Learning.
5. Tipler, s. (2006). Fysik för vetenskap och teknik. 5: e upplagan. Volym 1. Redaktör.