Integrationskonstant betydelse, beräkning och exempel

De Integrationskonstant Det är ett mervärde till beräkningen av antiderivativen eller integralerna, det tjänar till att representera de lösningar som utgör en primitiv för en funktion. Uttrycker en inneboende tvetydighet där någon funktion har ett oändligt antal primitiva.

Till exempel om funktionen tas: f (x) = 2x + 1 och vi får dess antiderivativ:

∫ (2x+1) dx = x² + x + C ; Var C Det är Integrationskonstant och representerar grafiskt den vertikala översättningen mellan de oändliga möjligheterna till primitiva. Det är korrekt att säga att (x² + x) det är en av den primitiva f (x).

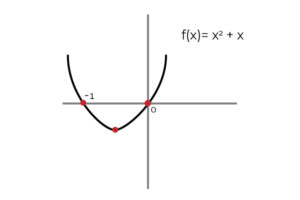Källa: Författare

På samma sätt kan du definiera (x² + x + C ) som primitiva för f (x).

[TOC]

Omvänd egendom

Det kan noteras att vid härledd uttrycket (x² + x) Funktionen f (x) = 2x + 1 erhålls. Detta beror på den omvända egenskapen mellan härledningen och integrationen av funktioner. Den här egenskapen gör det möjligt att få integrationsformler från differentiering. Vilket möjliggör verifiering av integraler genom samma derivat.

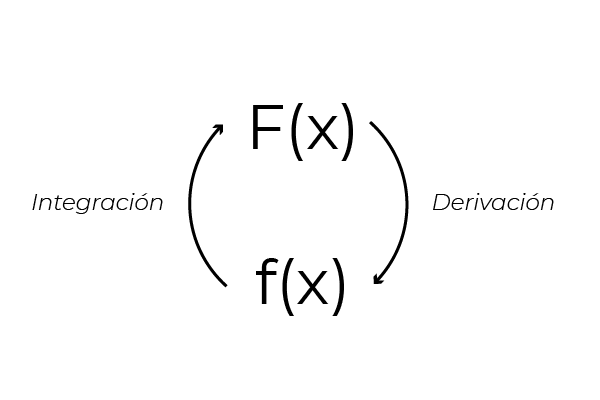Källa: Författare

Men (x² + x) Det är inte den enda funktionen vars derivat är lika med (2x + 1).

1. D (x² + x)/ dx = 2x + 1
2. D (x² + x + 1)/ dx = 2x + 1
3. D (x² + x + 2)/ dx = 2x + 1
4. D (x² + x + 3)/ dx = 2x + 1
5. D (x² + x + C)/ dx = 2x + 1

Där 1, 2, 3 och 4 representerar speciellt primitiva för f (x) = 2x + 1. Medan 5 representerar den obestämda eller primitiva integralen av f (x) = 2x + 1.

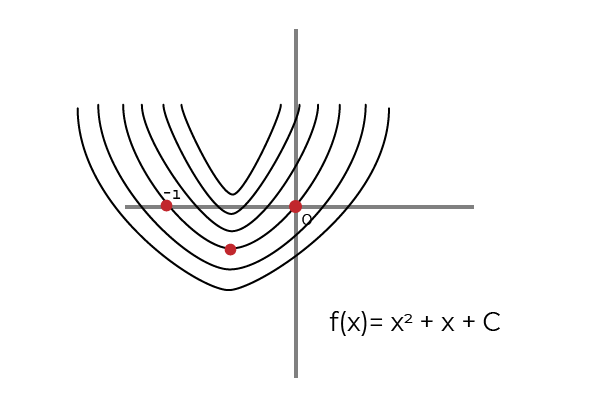Källa: Författare

Den primitiva för en funktion uppnås genom antiderivering eller integrerad process. Där f kommer att vara en primitiv f om följande är uppfyllt

• y = ∫ f (x) dx = F (x) + c; C = Integrationskonstant
• F '(x) = f (x)

Det uppskattas att en funktion har ett enda derivat, till skillnad från dess oändliga primitiva till följd av integration.

Den obestämda integrerade

 ∫ f (x) dx = f (x) + c

Det motsvarar en familj av kurvor med samma mönster, som upplever inkongruitet i värdet på bilderna på varje punkt (x, y). Varje funktion som uppfyller detta mönster kommer att vara en individuell primitiv och uppsättningen av alla funktioner kallas Obestämd integral.

Värdet på Integrationskonstant Det kommer att vara den som skiljer varje funktion i praktiken.

De Integrationskonstant Det föreslår en vertikal förskjutning i alla grafer som representerar den primitiva för en funktion. Där parallellism observeras mellan dem, och det faktum att C Det är värdet av förskjutning.

Enligt vanliga metoder Integrationskonstant Det betecknas med bokstaven “C” efter en tillägg, även om det i praktiken är likgiltig om konstanten lägger till eller subtraherar. Dess verkliga värde finns på olika sätt beroende på olika första villkor.

Andra betydelser av integrationskonstanten

Det var redan prat om hur Integrationskonstant appliceras i grenen av integrerad kalkyl; Representerar en familj av kurvor som definierar den obestämda integralen. Men många andra vetenskaper och filialer har tilldelat mycket intressanta och praktiska värden på Integrationskonstant, som har underlättat utvecklingen av flera studier.

Kan tjäna dig: rektangel trapezoid: egenskaper, relationer och formler, exempel

I fysisk Integrationskonstant kan ta flera värden beroende på datas art. Ett mycket vanligt exempel är att känna till funktionen V (t) som representerar fart av en partikel kontra tiden T. Det är känt att funktionen erhålls vid beräkning av en primitiv V (t) R (t) som representerar placera av partikeln kontra tid.

De Integrationskonstant kommer att representera värdet på den ursprungliga positionen, det vill säga just nu t = 0.

På samma sätt, om funktionen är känd A (t)  som representerar acceleration av partikeln kontra tid. Primitiva för en (t) kommer att resultera i funktion v (t), där Integrationskonstant Det kommer att vara värdet på den initiala hastigheten v₀.

I ekonomi, Genom att få primitiva för en kostnadsfunktion genom integration. De Integrationskonstant kommer att representera de fasta kostnaderna. Och så många andra applikationer som förtjänar differentiell och integrerad kalkyl.

Hur beräknas integrationskonstanten?

För beräkningen av Integrationskonstant, Det kommer alltid att vara nödvändigt att veta första villkor. Som ansvarar för att definiera vilken av den möjliga primitiva är motsvarande.

I många applikationer behandlas det som en oberoende variabel till tiden (t), där konstanten C ta de värden som definierar första villkor av det särskilda fallet.

Om det första exemplet tas: ∫ (2x+1) dx = x² + x + C

Ett giltigt initialt villkor kan vara att konditionera grafiken för att passera genom en specifik koordinat. Till exempel är det känt att primitiv (x² + x + C) Gå igenom punkten (1, 2)

F (x) = x² + x + C; Detta är den allmänna lösningen

F (1) = 2

Vi ersätter den allmänna lösningen i denna jämlikhet

F (1) = (1)² + (1) + C = 2

Där det lätt dras här C = 0

På detta sätt är motsvarande primitiva för detta fall F (x) = x² + x

Det finns olika typer av numeriska övningar som fungerar med Integrationskonstanter. Faktum är att differentiell och integrerad kalkyl inte upphör att tillämpas i nuvarande undersökningar. På olika akademiska nivåer kan du hitta; Från initial beräkning, genom fysik, kemi, biologi, ekonomi, bland andra.

Det uppskattas också i studien av differentiella ekvationer, där den Integrationskonstant Du kan ta olika värden och lösningar, detta på grund av flera hänvisningar och integrationer som genomförs i denna fråga.

Exempel

Exempel 1

1. En kanon som ligger 30 meter höga skott vertikalt upp en projektil. Det är känt att den initiala projektilhastigheten är 25 m/s. Bestämma:

• Funktionen som definierar projektilens position med avseende på tid.
• Flygtid eller tid då partikeln spelar marken.

Det kan tjäna dig: de åtta typerna av mätfel (med exempel)

Det är känt att i en enhetligt varierad rektilinär rörelseacceleration är ett konstant värde. Detta är fallet med projektillanseringen, där accelerationen kommer att vara tyngdkraft

G = - 10 m/s²

Det är också känt att acceleration är det andra härrörande från positionen, vilket indikerar en dubbel integration i upplösningen av övningen och därmed erhåller två Integrationskonstanter.

A (t) = -10

V (t) = ∫a (t) dt = ∫ (-10t) dt = -10T + C₁

Övningsvillkoren för övningen indikerar att den initiala hastigheten är v₀ = 25 m/s. Detta är hastigheten vid tiden t = 0. På detta sätt är det uppfyllt att:

V (0) = 25 = -10 (0) + C₁   och C₁ = 25

Hastighetsfunktionen definieras

V (t) = -10t + 25; Du kan se likheten med MRUV -formeln (v_F = V₀ + A x t)

I homolog är hastighetsfunktionen integrerad för att uppnå uttrycket som definierar positionen:

R (t) = ∫v (t) dt = ∫ (-10t+25) dt = -5t² + 25T + C₂

R (t) = -5t² + 25T + C₂  (Primitiv position)

Den initiala positionen r (0) = 30 m är känd. Då beräknas projektilens speciella primitiva.

R (0) = 30m = -5 (0)² + 25 (0) + C₂ . Var C₂ = 30

Det första avsnittet är löst sedan R (t) = -5t² + 25t + 30  ; Detta uttryck är homologt med förskjutningsformeln i mruv r (t) = r₀ + V₀T - gt²/2

För det andra avsnittet måste den kvadratiska ekvationen lösas: -5T² + 25t + 30 = 0

Eftersom det villkorar partikeln att nå marken (position = 0)

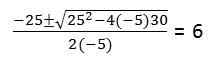Källa: Författare

Egentligen kastar 2: a -ekvationen 2 lösningar t: 6, -1. Värdet t = -1 ignoreras eftersom det är tidsenheter vars domän inte inkluderar negativa siffror.

På detta sätt löses det andra avsnittet där flygtiden är lika med 6 sekunder.

Exempel 2

2. Hitta den primitiva f (x) som uppfyller de initiala förhållandena:

• f "(x) = 4; f '(2) = 2; f (0) = 7

Med informationen om det andra derivatet F "(x) = 4 börjar antideriveringsprocessen

f '(x) = ∫f "(x) dx

∫4 dx = 4x + c₁

Sedan känner du till villkoret f '(2) = 2:

4 (2) + c₁ = 2

C₁ = -6 och f '(x) = 4x - 8

Fortsätt på samma sätt för den andra Integrationskonstant

f (x) = ∫f '(x) dx
∫ (4x - 8) dx = 2x² - 8x + c₂

Det initiala villkoret F (0) = 7 är känt och fortsätt:

2 (0)² - 8 (0) + c₂ = 7

C₂ = 7 och f (x) = 2x² - 8x + 7

• f "(x) = x² ; f '(0) = 6; f (0) = 3

I likhet med det tidigare problemet definierar vi de första derivaten och den ursprungliga funktionen från de initiala förhållandena.

f '(x) = ∫f "(x) dx

∫ (x²) Dx = (x³/3) + c₁

Med tillstånd f '(0) = 6 intäkter:

Kan tjäna dig: Set Theory: Egenskaper, element, exempel, övningar

(0³/3) + c₁ = 6; Var₁ = 6 och f '(x) = (x³/3) + 6

Sedan den andra Integrationskonstant

f (x) = ∫f '(x) dx

∫ [(x³/3) + 6] dx = (x⁴/12) + 6x + c₂

Det initiala villkoret F (0) = 3 är känt och fortsätt:

[(0)⁴/12] + 6 (0) + c₂ = 3; Var₂ = 3

Den speciella primitiva erhålls

f (x) = (x⁴/12) + 6x + 3

Exempel 3

3. Definiera de primitiva funktionerna med tanke på derivaten och en punkt i grafen:

• dy/dx = 2x - 2 som passerar genom punkten (3, 2)

Det är viktigt att komma ihåg att derivaten hänvisar till lutningen av linjen tangent till kurvan vid en viss punkt. Där det inte är korrekt att anta att grafiken för derivatet berör den angivna punkten, eftersom den tillhör grafen för den primitiva funktionen.

På detta sätt uttrycker vi differentiell ekvation på följande sätt:

dy = (2x - 2) dx  ; Sedan när du tillämpar antiderivationskriterierna har du:

∫dy = ∫ (2x - 2) dx

y = x² - 2x + c

Tillämpa det initiala tillståndet:

2 = (3)² - 2 (3) + c

C = -1

Erhålles: f (x) = x² - 2x - 1

• dy/dx = 3x² - 1 som passerar genom punkten (0, 2)

Vi uttrycker differentiell ekvation på följande sätt:

dy = (3x² - 1) dx  ; Sedan när du tillämpar antiderivationskriterierna har du:

 ∫dy = ∫ (3x² - 1) dx

y = x³ - x + c

Tillämpa det initiala tillståndet:

2 = (0)² - 2 (0) + c

C = 2

Erhålles: f (x) = x³ - x + 2

Föreslagna övningar

Övning 1

1. Hitta den primitiva f (x) som uppfyller de initiala förhållandena:

• f "(x) = x; f '(3) = 1; f (2) = 5
• f "(x) = x + 1; f '(2) = 2; f (0) = 1
• f "(x) = 1; f '(2) = 3; f (1) = 10
• f "(x) = -x; f '(5) = 1; f (1) = -8

Övning 2

2. En ballong som stiger med 16 fot/s hastighet släpper ut en sandjacka från en höjd av 64 fot över marknivån.

• Definiera flygtid
• Vad blir vektorn V_F När du rör vid golvet?

Övning 3

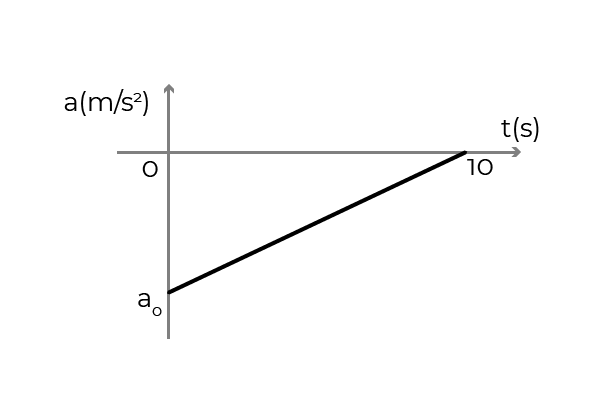
3. Figuren visar accelerationsgrafen - tiden för en bil som rör sig i x -axelns positiva mening. Bilen reser till en konstant hastighet på 54 km/h när föraren applicerade bromsarna för att stanna på 10 sekunder. Bestämma:

• Den första accelerationen av bilen
• Bilhastigheten vid t = 5s
• Förskjutningen av bilen under bromsning

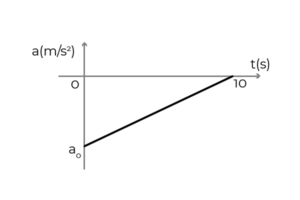Källa: Författare

Övning 4

4. Definiera de primitiva funktionerna med tanke på derivaten och en punkt i grafen:

• dy/dx = x som passerar genom punkten (-1, 4)
• dy/dx = -x² + 1 som går igenom punkten (0, 0)
• dy/dx = -x + 1 som passerar genom punkten (-2, 2)

Referenser

1. Integrerad kalkyl. Indefinied Integrations- och integrationsmetoder. Wilson, Velásquez Bastidas. Magdalena 2014 University
2. Stewart, J. (2001). Beräkning av en variabel. Tidig transcendent. Mexiko: Thomson Learning.
3. Jiménez, r. (2011). Matematik VI. Integrerad kalkyl. Mexiko: Pearson Education.
4. Fysik i. MC Graw Hill