Konstanter av antoinformler, ekvationer, exempel

De antoin Det finns tre parametrar som visas i ett empiriskt samband mellan mättnadsångtryck och temperatur för rena ämnen. De är beroende av varje ämne och ska vara konstant i ett visst temperaturintervall.

Ut ur det intervallet förändrar konstanterna för antoin deras värde. Konstanterna är relaterade genom en ekvation som skapades 1888 av den franska ingenjören Louis Charles Antoine (1825-1897).

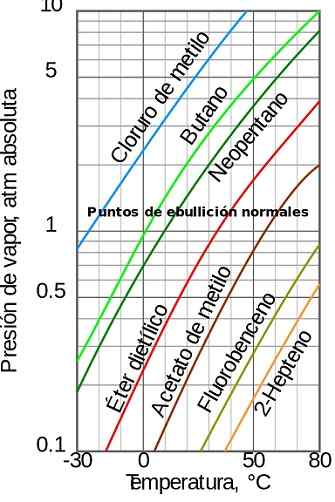
Figur 1. Ångtryck beroende på temperaturen. Källa: Wikimedia Commons

[TOC]

Formler och ekvationer

Det vanligaste sättet att uttrycka Antoines funktion är:

 

I denna formel P representerar den mättnadsånga tryck uttryckt i kvicksilver millimeter (MMHg), t är temperaturen som är den oberoende variabeln och uttrycks i ℃. 

A, B och C är konstanter eller parametrar för antoinformeln.

Betydelsen av denna formel som trots att det är empiriskt ger ett enkelt analytiskt uttryck som lätt kan användas i termodynamiska beräkningar.

Antoines formel är inte unik, det finns mer exakta uttryck som är förlängningar av denna formel, men med nackdelen som har sex eller fler parametrar och deras matematiska uttryck är mer komplexa, vilket gör dem mycket metoder att använda i de termodynamiska beräkningarna.

Mättnadsånga

När Antoines formel mäter mättnadsångtryck är det nödvändigt att förklara vad den består av.

I ett glas ampull eller annan behållare placeras en vätska. All luftluft extraheras. Uppsättningen placeras i ett termiskt bad tills balansen har uppnåtts.

I början är allt flytande, men eftersom det finns ett vakuum börjar de snabbaste molekylerna att överge vätskan och bilda en gas med samma substans i vätskan.

Kan tjäna dig: enhetlig rätlinjig rörelse: egenskaper, formler, övningar

Den föregående processen är avdunstning Och när ångtrycket ökar. 

Några av ångmolekylerna förlorar energi och återgår till den flytande fasen i ämnet, detta är processen för kondensation.

Sedan inträffar två processer, indunstning och kondensation samtidigt. När samma antal flytande molekyler som är integrerade i det kommer ut, a dynamisk balans Och vid denna tidpunkt inträffar det maximala ångtrycket som kallas mättnadstryck.

Det är detta ångmättnadstryck som förutsäger antoinformeln för varje substans och varje temperatur.

I vissa fasta ämnen finns det ett liknande fenomen när det passerar från den fasta fasen till soda direkt utan att gå igenom vätskefasen, i dessa fall kan en mättnadsånga tryck också mätas.

Det är inte lätt att etablera en teoretisk modell som börjar från tidiga principer eftersom förändringar i molekylär kinetisk energi är involverade, vilket kan vara av translationell, rotations- och vibrationstyp, med den inre molekylära bindningen energi. Det är av detta skäl som empiriska formler i praktiken används.

Hur är konstanten av Antoine?

Det finns ingen teoretisk metod för att erhålla antoinens konstanter, eftersom det är en empirisk relation.

De erhålls från experimentella data för varje ämne och justerar de tre parametrarna A, B och C, så att de minimerar den kvadratiska skillnaden (metoden för kvadratminimum) för förutsägelsen med experimentella data.

För slutanvändaren, som i allmänhet är kemiska ingenjörer, finns det tabeller i kemihandböckerna där dessa konstanter ges för varje ämne som indikerar maximalt och minimitemperaturområden där de är tillämpliga.

Kan tjäna dig: Motståndstermometer: Egenskaper, drift, användningar

Onlinetjänster finns också tillgängliga som ger värdena på konstanterna A, B och C som är fallet med DDBST GmbH onlines -tjänster.

För samma ämne kan det finnas mer än ett giltighetstemperaturområde. Beroende på arbetsområdet väljs en eller annan grupp konstanter.

Svårigheterna kan förekomma om temperaturarbetsområdet är mellan två giltighetsintervall för konstanterna, eftersom förutsägelserna för formeltryck inte sammanfaller i gränszonen.

Exempel

Exempel 1

Hitta vattenångtrycket vid 25 ℃.

Lösning 

Vi konsulterade tabellerna för att bestämma konstanterna för Antoine.

Det finns två vattenintervall: 

Mellan 1 ℃ och 100 ℃ och mellan 99 ℃ till 374 ℃.

Eftersom vi är intresserade av 25 ℃ tar vi det första intervallet där värdet på Antoines konstanter är:

A = 8.07131

B = 1730,63

C = 233,426

P = 10^(8 07131 - 1730,63/(25 + 233,426)))

Exponentens beräkning

Låt oss beräkna exponenten först: 1 374499

P = 10^1 374499 = 23,686 mmHg = 0,031166 ATM

Resultatanalys

Detta resultat tolkas på följande sätt:

Anta att rent vatten placeras i en hermetisk behållare som luften har extraherats av en vakuumpump.

Behållaren med vatten placeras i ett termiskt bad vid en temperatur på 25 ℃ tills den termiska jämvikten når.

Vatten i den hermetiska behållaren avdunstar delvis tills mättnadsångtrycket har uppnåtts, vilket inte är något annat än trycket i vilket den dynamiska balansen mellan vätskefasen i vattnet och ångfasen fastställs. 

Kan tjäna dig: Dirac Jordan Atomic Model: Egenskaper och postulat

Det trycket i detta fall visade sig vara 0,031166 ATM vid 25 ℃.

Exempel 2

Hitta vattenångtrycket vid 100 ℃.

Lösning 

Vi konsulterade tabellerna för att bestämma konstanterna för Antoine. Det finns två vattenintervall: 

Mellan 1 ℃ och 100 ℃ och mellan 99 ℃ till 374 ℃.

I detta fall är temperaturen av intresse i de två områdena.

Vi använder den första av områdena [1 ℃, 100 ℃]

A = 8.07131

B = 1730,63

C = 233,426

P = 10^(8 07131 - 1730,63/(100 + 233,426)))

Exponentens beräkning

Låt oss först beräkna exponenten: 2.8808

P = 10^1 374499 = 760,09 mmHg = 1 0001 atm

Därefter använder vi den andra av områdena [99 ℃, 374 ℃]

I detta fall är konstanterna

A = 8.14019

B = 1810.94

C = 244.485

P = 10^(8.14019 - 1810.94/(100 + 244.485)))

Låt oss först beräkna exponenten: 2.88324

P = 10^2.88324 = 764.2602 mmHg = 1,0056 atm

Det finns en procentuell skillnad mellan de två resultaten av 0,55%.

Referenser

1. Tillämpning av lagarna i Raoult och Dalton och Antoine -ekvationen. Hämtad från: min egen och forntida.WordPress.com
2.  Online -kalkylator för antoinformeln. Återhämtat sig från: ddbonline.Ddbst.av/antoinecalcion/antoinecalculaticgi.exe
3. Gecousb. Termodynamik och ångtabeller / konstant från Antoine. Återhämtat sig från: gecousb.com.gå
4. Materiets termiska egenskaper. Återhämtat sig från: webbserver.Dmt.UPM.är
5. Yaws och Yang. Antoinkonstantbord för mer än 700 organiska föreningar. Återhämtat sig från: användare.Göra.Umd.Edu
6. Wikipedia. Antoineekvation. Återhämtat sig från Wikipedia.com
7. Wikipedia. Clausius-Clapeyron-ekvation. Återhämtat sig från Wikipedia.com
8. Wisniak J. Historisk utveckling av ångtryckekvationen från Dalton Toy Antoine. Återhämtad från: länk.Kandare.com