Humöriga diagramekvationer, vad är det för, applikationer

han Humördiagram Den består av en serie kurvor ritade på logaritmiskt papper, som används för att beräkna den friktionsfaktor som finns i flödet av en turbulent vätska genom en cirkulär kanal.

Med friktionsfaktorn F Förlusten av friktionsenergi utvärderas, ett viktigt värde för att bestämma rätt prestanda för pumparna som fördelar vätskor som vatten, bensin, råolja.

Rör på industriell nivå. Källa: Pixabay.

Att känna energin i flödet av en vätska är det nödvändigt och rörets väggar.

[TOC]

Ekvationer för en rörelsevätska

Mellan två delar av ett rör, betecknade som 1 och 2, Det är möjligt att upprätta följande balans, som är en utvidgning av Bernoulli -ekvationen: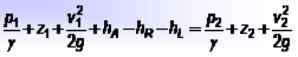Var:

- p₁ och p₂ är trycket vid varje punkt,

- z₁ och z₂ är höjderna med avseende på en referenspunkt,

- v₁ och v₂ är respektive vätskehastighet,

- h_TILL Det är den energi som läggs till av pumpar, h_R Det är den energi som en enhet tagit som en motor, och h_L Det täcker vätskenergiförlusterna på grund av friktion mellan detta och rörens väggar, liksom andra mindre förluster.

Värdet av h_L Det beräknas med Darcy-Weisbach-ekvationen:

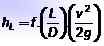
Var L Det är rörets längd, D Det är dess inre diameter, v Det är vätskans hastighet och g Det är värdet på tyngdkraften. Dimensioner av h_L De är långa, och vanligtvis är de enheter som den representeras är meter eller fötter.

-Friktionsfaktor och Reynolds nummer

Att beräkna F Empiriska ekvationer erhållna från experimentella data kan användas. Det är nödvändigt att skilja om det är en vätska i laminär regim eller turbulent regim. För den laminära regimen F Det utvärderas lätt:

F = 64/n_R

Var N_R Det är Reynolds -numret, vars värde beror på regimen där vätskan är belägen. Kriterierna är:

Laminärt flöde: n_R < 2000 el flujo es laminar; Flujo turbulento N_R > 4000; Övergångsregime: 2000 < N_R < 4000

Reynolds nummer (dimensionlöst) beror i sin tur på vätskehastighet v, Den inre diametern på rörledningen D och den kinematiska viskositeten n av vätskan, vars värde erhålls med tabeller:

Kan tjäna dig: enhetligt accelererad rätlinjig rörelse: egenskaper, formler

N_R = v.D /n

Colebrook ekvation

För ett turbulent flöde är den mest accepterade ekvationen i koppar- och glasrör den för Cyril Colebrook (1910-1997), men det har besväret som F Det är inte uttryckligt:

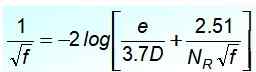
I denna ekvation e/d Det är rörets relativa grovhet och N_R Det är Reynolds -numret. När du observerar det noggrant märks det att det inte är lätt att lämna F På vänster sida av jämlikhet, så det är inte bekvämt för omedelbara beräkningar.

Colebrook föreslog själv detta tillvägagångssätt som är uttryckligt, giltigt med vissa begränsningar:

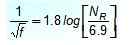
Vad är det för?

Moodys diagram är användbart för att hitta friktionsfaktor F ingår i Darcy -ekvationen med tanke på att det i Colebrook -ekvationen inte är lätt att uttrycka F direkt i termer av andra värden.

Dess användning förenklar att få värdet av F, genom att innehålla den grafiska representationen av F i funktion av N_R För olika värden på relativ grovhet i en logaritmisk skala.

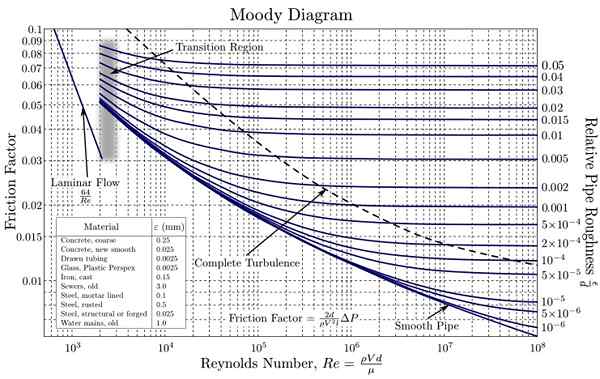Humördiagram. Källa: https: // ladda upp.Wikimedia.org/wikipedia/commons/d/d9/Moody_en.Svg

Dessa kurvor har skapats av experimentella data med olika material som vanligtvis används i rörtillverkning. Användning av en logaritmisk skala båda för F som för N_R Det är nödvändigt, eftersom de täcker ett mycket brett spektrum av värden. På detta sätt underlättas graferingen av värden på olika storleksordningar.

Den första grafen av Colebrook-ekvationen erhölls av ingenjör Hunter Rouse (1906-1996) och strax efter modifierades av Lewis F. Moody (1880-1953) på det sätt som det används för närvarande.

Det används för både cirkulära och icke -cirkulära rör, det räcker för att ersätta den hydrauliska diametern för dessa.

Hur görs det och hur det används?

Som förklarats ovan är det humöriga diagrammet tillverkat av många experimentella data, presenterade grafiskt. Här är stegen för att använda det:

- Beräkna Reynolds -numret N_R För att avgöra om flödet är laminärt eller turbulent.

- Beräkna relativ grovhet genom ekvation och_r = E/d, var och Det är den absoluta grovheten hos materialet och D är rörets inre diameter. Dessa värden erhålls med tabeller.

- Nu när det är tillgängligt och_r och N_R, projekt vertikalt tills den når kurvan som motsvarar och_r erhållen.

- Projekt horisontellt och till vänster för att läsa värdet av F.

Ett exempel kommer lätt att visualisera hur diagrammet används.

Kan tjäna dig: kalciumfluorid (CAF2): struktur, egenskaper, användningar

-Löst exempel 1

Bestäm vattenfriktionsfaktorn vid 160 ° F som flyter med en hastighet av 22 fot/s i en kanal gjord av icke -belagda smidesjärn och inre diameter på 1 tum.

Lösning

Nödvändiga data (finns i tabellerna):

Vattenkinematisk viskositet vid 160 ºF: 4.38 x 10^-6 fot²/s

Absolut grovhet av smidesjärn inte täckt: 1.5 x 10 ^-4 fötter

Första steget

Reynolds -numret beräknas, men inte innan du passerar den inre diametern på 1 tum vid foten:

1 tum = 0.0833 fot

N_R = (22 x 0.0833)/ 4.38 x 10^-6= 4.18 x 10 ⁵

Enligt kriterierna som visas innan det är ett turbulent flöde, gör det humöriga diagrammet att motsvarande friktionsfaktor kan erhållas, utan att behöva använda Colleebrook -ekvationen.

Andra steg

Du måste hitta relativ grovhet:

och_r = 1.5 x 10 -4 / 0.0833 = 0.0018

Tredje steg

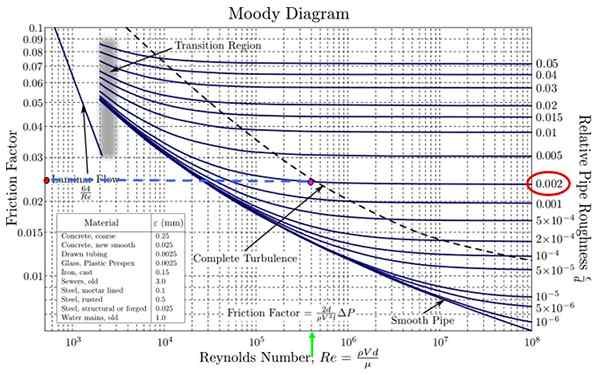
I det humöriga diagrammet är det nödvändigt. Det finns ingen som motsvarar exakt vid 0.0018 men det finns en som närmar sig mycket, 0.002 (figurens röda oval).

Samtidigt söks motsvarande Reynolds -nummer på den horisontella axeln. Värdet som är mest liknar 4.18 x 10 ⁵ är 4 x 10 ⁵ (Grön pil i figuren). Korsningen mellan båda är fuchsia -punkten.

Fjärde steget

Projekt kvar till vänster prickade linje och komma till den orange punkten. Nu uppskattar värdet på F, Med hänsyn till att uppdelningar inte har samma storlek som det är en logaritmisk skala både i horisontella och vertikala axeln.

Det humöriga diagrammet som levereras i figuren har inte fina horisontella divisioner, så värdet på F i 0.024 (är mellan 0.02 och 0.03 men det är inte hälften men lite mindre).

Det finns online -kalkylatorer som använder Colleebrook -ekvationen. En av dem (se referenser) medföljande värde 0.023664639 för friktionsfaktor.

Ansökningar

Det humöriga diagrammet kan appliceras för att lösa tre typer av problem, förutsatt att rörets flytande och absoluta grovhet är kända:

- Beräkning av tryckfallet eller skillnaden i tryck mellan två punkter, tillförde rörets längd, höjdskillnaden mellan de två punkter som ska beaktas, hastigheten och rörets inre diameter.

Kan tjäna dig: pendular rörelse

- Bestämning av flödet, känd längden och diametern på röret, plus det specifika tryckfallet.

- Utvärdering av rörets diameter när längden, flödesfallet mellan de punkter som ska vara kända är kända.

Problemen med den första typen löses direkt genom att använda diagrammet, medan de av den andra och tredje typen kräver användning av ett beräkningspaket. Till exempel, i de tredje typen, om rörets diameter inte är känd, kan Reynolds -numret inte utvärderas direkt, och inte heller den relativa grovheten.

Ett sätt att lösa dem är att anta en initial inre diameter och därifrån justerar successivt värdena för att få det tryckfall som anges i problemet.

-Löst exempel 2

Det har vatten vid 160 ° F flytande parkerat längs ett 1 -tum rör i smidesjärndiameter som inte täcks, med en hastighet av 22 fot/s. Bestäm tryckskillnaden orsakad av friktion och pumpkraft som krävs för att upprätthålla flödet i en horisontell rör av l = 200 fot lång.

Lösning

Nödvändiga data: Acceleration av tyngdkraften är 32 fot/s² ; Vattenens specifika vikt vid 160 ºF är y = 61.0 lb-kraft/fot³

Detta är röret i exemplet löst 1, därför är friktionsfaktorn redan känd F, som har uppskattats till 0.0024. Detta värde tas till Darcy -ekvationen för att utvärdera friktionsförluster:

Den nödvändiga pumpkraften är:

W = v. TILL. (p₁ - p₂)

Där a är rörets tvärsnitt: a = p. (D²/4) = p. (0.0833²/4) fot² = 0.00545 fot²

W = 22 fot /s . 2659.6 pund-kraft / fot². 0.00545 fot²= 318.9 pund-kraft . fötter

Kraften uttrycks bättre i watt, för vilken omvandlingsfaktorn krävs:

1 watt = 0.737 lb-kraft . fötter

Därför är den kraft som krävs för att upprätthålla flödet W = 432.7 w

Referenser

1. Cimbala, c. 2006. Mekanik för vätskor, grundläggande faktorer och applikationer. Mc. Graw Hill. 335-342.
2. Franzini, J. 1999. Fluid Mechanics With Application är inom teknik. Mc. Graw Hill.176-177.
3. LMNO -teknik. Humör friktionskalkylatorfaktor. Återhämtat sig från: lmnoeng.com.
4. Mott, r.  2006. Flytande mekanik. 4th. Utgåva. Pearson Education. 240-242.
5. Teknisk verktygslåda. Humördiagram. Återhämtat sig från: EngineeringToolbox.com
6. Wikipedia. Humördiagram. Återhämtad från: in.Wikipedia.org