Radiell belastning Hur beräknas, lösta övningar

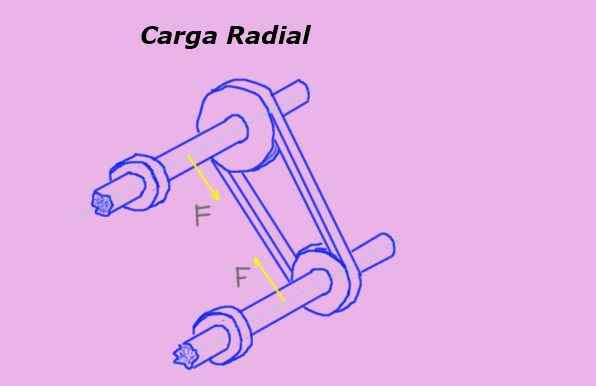
De Radiell belastning Det är kraften som utövas vinkelrätt mot ett objekts symmetri och vars handlingslinje passerar genom denna axel. Till exempel påför ett bälte på en remskiva en radiell belastning på lagret eller lagret på samma axel.

I figur 1 representerar de gula pilarna radiella krafter på axlarna på grund av bältets spänning som passerar genom remskivorna.

Figur 1. Radiell belastning på remskivor. Källa: Självgjord.

Måttenheten på den radiella belastningen i det internationella systemet eller om det är Newton (N). Men andra kraftenheter används också för att mäta det, såsom kilogramkraften (KG-F) och pundstyrkan (LB-F).

[TOC]

Hur beräknas det? 

För att beräkna värdet på den radiella belastningen i elementen i en struktur måste följande steg följas:

- Gör kraftdiagrammet på varje element.

- Tillämpa ekvationerna som garanterar translationsbalansen; det vill säga summan av alla krafter är noll.

- Tänk på ekvationen av vridmoment eller stunder så att rotationsbalansen uppfylls. I detta fall måste summan av alla moment vara noll.

- Beräkna krafterna för att identifiera de radiella belastningarna som verkar i vart och ett av elementen.

Löst övningar

-Övning 1

Följande figur visar en remskiva genom vilken en spänd remskiva passerar med spänning T. Remskivan är monterad på en axel som vilar på två chumaceras. Mitten av en av dem är på avstånd L₁ från mitten av remskivan. I andra änden är den andra chumacera, på ett avstånd L₂.

Kan tjäna dig: higroskopicitet: koncept, hygroskopiska ämnen, exempel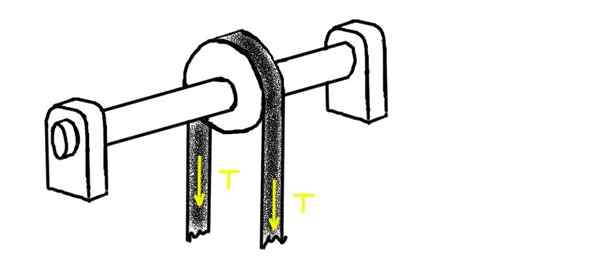figur 2. Remskiva genom vilken en spänd rem passerar. Källa: Självgjord.

Bestäm den radiella belastningen på var och en av chumaceras, förutsatt att axeln och remskivans vikt är ganska lägre än den applicerade spänningen.

Ta som värde för 100 kg-f-remspänningen och för avstånd l₁= 1 m och l₂= 2 m.

Lösning

För det första är ett diagram över krafterna som verkar på axeln.

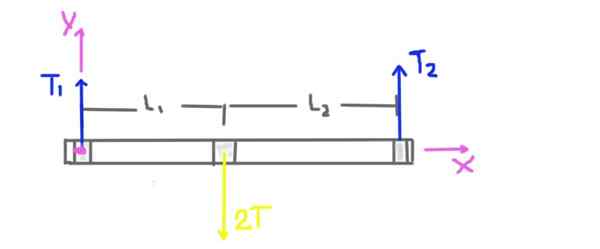Figur 3. Träningskraftdiagram 1.

Remskivan är T, men den radiella belastningen på axeln i remskivans läge är 2T. Vikten på axeln och remskivan beaktas inte eftersom problemuttalandet säger att det är mycket lägre än spänningen som appliceras på bältet.

Stödstödets radiella reaktion orsakas av radiella krafter eller belastningar T1 och T2. Avståndet L1 och L2 för stödet till remskivans centrum anges också i diagrammet.

Koordinatsystemet visas också. Vridmomentet eller det totala ögonblicket på axeln kommer att beräknas ta som ett centrum för koordinatsystemets ursprung och kommer att vara positivt i z -riktningen.

Jämviktsförhållanden

Jämviktsförhållandena är nu etablerade: summan av samma noll och summan av moment är lika noll.

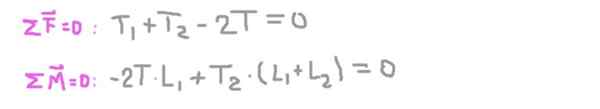
Från den andra ekvationen den radiella reaktionen på axeln på stöd 2 (t₂), ersätta i den första och rensa den radiella reaktionen på axeln i stöd 1 (t₁).

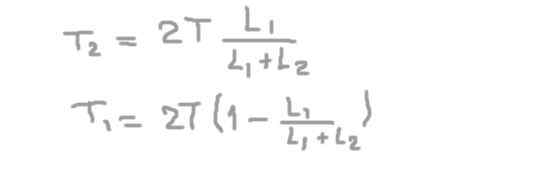Om vi ​​ersätter de numeriska uppgifterna får vi att den radiella belastningen eller kraften på axeln i positionen för support 1 är:

T₁= (2/3) t = 66,6 kg-f

Det kan tjäna dig: kalibreringskurva: vad är det för, hur man gör det, exempel

Och den radiella belastningen på axeln i stöd av Support 2 är:

T₂= (4/3) t = 133,3 kg-f.

Övning 2

Följande figur visar ett system som består av tre remskivor A, B, C alla Radio R. Remskivorna är anslutna med ett bälte som har en T -spänning.

Axlar A, B, C passerar smörjlager. Separationen mellan axlarna A och B är 4 gånger radien R. På liknande sätt är separationen mellan axlarna B och C också 4R.

Bestäm den radiella belastningen på remskivans axlar A och B, förutsatt att bältets spänning är 600N.

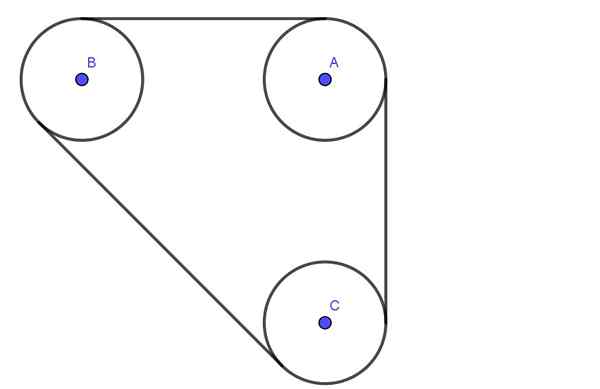Figur 4. Remssystem. Övning 2. (Egen utarbetande)

Lösning

Det börjar med att rita ett diagram över krafterna som verkar på remskiva A och B. Den första har du båda t spänningarna₁ och t₂, liksom kraften f_TILL Att lagret utövar på remskivans axel.

På samma sätt har du på remskiva₃ , T₄ och kraften f_B att lagret utövar på samma axel. Den radiella belastningen på remskivans axel är kraften f_TILL och den radiella belastningen på B är kraften f_B.

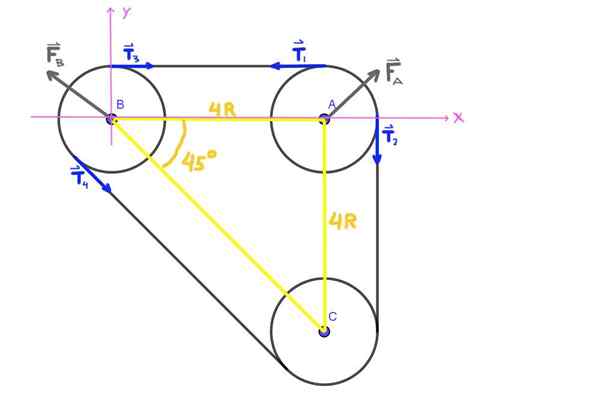Figur 5. Kraftsdiagram, övning 2. (Egen utarbetande)

Eftersom axlar a, b, c bildar en isorektangel triangel är ABC -vinkeln 45 °.

Alla spänningar t₁ , T₂ , T₃ , T₄ visas i figuren har samma modul t, som är bältesspänningen.

Balansförhållanden för remskiva a

Nu skriver vi balansvillkoret för remskivan som det inte är något annat än summan av all kraft som verkar på remskivan och måste vara ogiltig.

Att separera komponenterna x och y från krafterna och lägga till (vektoriellt) följande par skalekvationer erhålls:

Kan tjäna dig: Titan (satellit)

F_TILLX - T = 0; F_TILLOCH - T = 0

Dessa ekvationer leder till följande jämlikhet: f_Yxa = F_ÅH = T.

Därför har den radiella belastningen storlek som ges av:

F_TILL = (T² + t²)^1/2 = 2^1/2∙ t = 1,41 ∙ t = 848,5 n. 45 ° riktning. 

Balanstillstånd för remskiva B

På liknande sätt skriver vi jämviktstillståndet för remskivor. För komponent X har du: f_BX + T + T ∙ COS45 ° = 0

Och för komponenten y: f_BOCH + T ∙ Sen45 ° = 0

Således:

F_Bx = - t (1+2^-1/2) och f_Förbi = -T ∙ 2^-1/2

Det vill säga storleken på den radiella belastningen på remskivan är:

F_B = ((1+2^-1/2) ² + 2^-1)^1/2∙ t = 1,85 ∙ t = 1108,66 n och dess adress är 135 °.

Referenser

1. Beer F, Johnston E, DeWolf J, Mazurek, D. Materialmekanik. Femte upplagan. 2010. MC Graw Hill. 1-130.
2. Gere J, Goodno, B. Materialmekanik. Åttonde upplagan. Cengage Learning. 4-220.
3. Giancoli, D. 2006. Fysik: Principer med applikationer. 6^Tth Ed. Prentice hall. 238-242.
4. Hibbeler R. Materialmekanik. Åttonde upplagan. Prentice hall. 2011. 3-60.
5. Valera Negrete, J. 2005. Allmänna fysikanteckningar. Unk. 87-98.