Sfäriska koordinater exempel och övningar löst

De sfäriska koordinater De är ett punktplatssystem i det tre dimensionella utrymmet som består av en radiell koordinat och två vinkelkoordinater som kallas polära koordinat och azimutal koordinat.

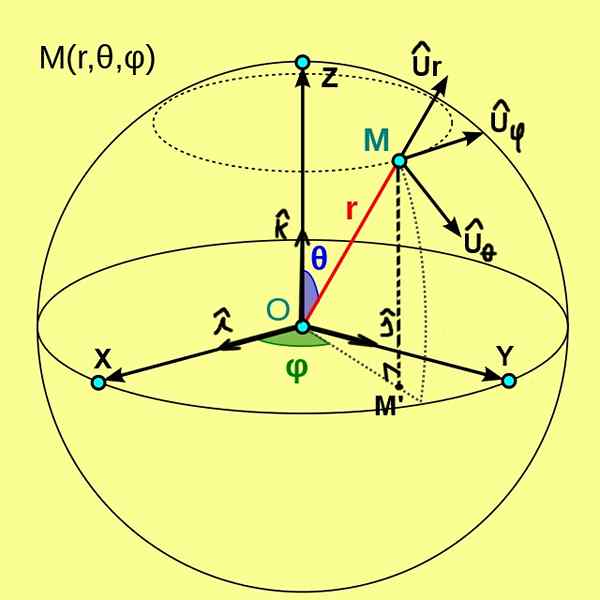
I figur 1, som vi ser nedan, visas de sfäriska koordinaterna (r, θ, φ) för en punkt m. Dessa koordinater hänvisas till ett ortogonalt system av kartesiska axlar x, y, z av ursprung eller.

Figur 1. Sfäriska koordinater (R, θ, φ) från en punkt M. (Wikimedia Commons)

I detta fall är koordinaten R för punkt M avståndet från den punkten till ursprunget eller. Den polära koordinaten θ representerar vinkeln mellan den positiva semi -axeln z och vektorradie om. Medan den azimutala koordinaten φ är vinkeln mellan den positiva semi -axeln x och vektorradie om ', är m' den ortogonala projektionen av m på XY -planet.

Den radiella koordinaten r tar bara positiva värden, men om en punkt är belägen vid ursprunget så är r = 0. Den polära koordinaten θ tar som ett minimivärde 0º för punkter som ligger på den positiva semi -tribben. Slutligen tar den azimutala koordinaten φ som ett minimivärde 0º och maximalt 360 ° nivå.

0 ≤ r < ∞

0 ≤ θ ≤ 180º ≤

0 ≤ φ  < 360º

[TOC]

Förändring av koordinater

Därefter kommer formlerna som tillåter de kartesiska koordinaterna (x, y, z) för en punkt m att ges, förutsatt att de sfäriska koordinaterna för samma (r, θ, φ) punkt:

x = r sen (θ) cos (φ)

y = r sen (θ) sin (φ) 

z = r cos (θ)

På samma sätt är det användbart att hitta relationerna att flytta från de kartesiska koordinaterna (x, y, z) för en punkt som ges till de sfäriska koordinaterna för den punkten:

R = √ (x^2 + y^2 + z^2)

θ = arcan (√ (x^2 + y^2) / z)

Kan tjäna dig: diskret slumpmässig variabel

φ = arctan (y / x)

Vektorbas i sfäriska koordinater

Från de sfäriska koordinaterna definieras en ortonormal basvektorer, som betecknas av Ur, Uθ, Uφ. Figur 1 visar dessa tre enhetsvektorer, som har följande egenskaper:

- Ur Det är enhetsvektorn tangent till den radiella linjen θ = ctte och φ = ctte;

- Uθ Det är enhetens tangentvektor till bågen φ = ctte och r = ctte;

- Uφ Det är den enhetliga vektortangenten till båge r = ctte och θ = ctte.

Linje- och volymelement i sfäriska koordinater

Vektorpositionen för en punkt i rymden i sfäriska koordinater är skriven så här:

r = r Ur

Men en oändlig variation eller förskjutning av en punkt i det tre dimensionella utrymmet, i dessa koordinater uttrycks det av följande vektorförhållande:

dr = Dr Ur + r dθ Uθ + r sen (θ) dφ Uφ

Slutligen skrivs en infinitesimal volym DV i de sfäriska koordinaterna så här:

dv = r^2 sin (θ) dr dθ dφ

Dessa förhållanden är mycket användbara för beräkning av linjeintegraler och volym i fysiska situationer som har sfärisk symmetri.

Förhållande till geografiska koordinater

Geografiska koordinater förstås att de tjänar till att hitta platser på jordens yta. Detta system använder koordinaterna för latitud och längd för att hitta positionen på jordens yta.

I det geografiska koordinatsystemet antas jordens yta.

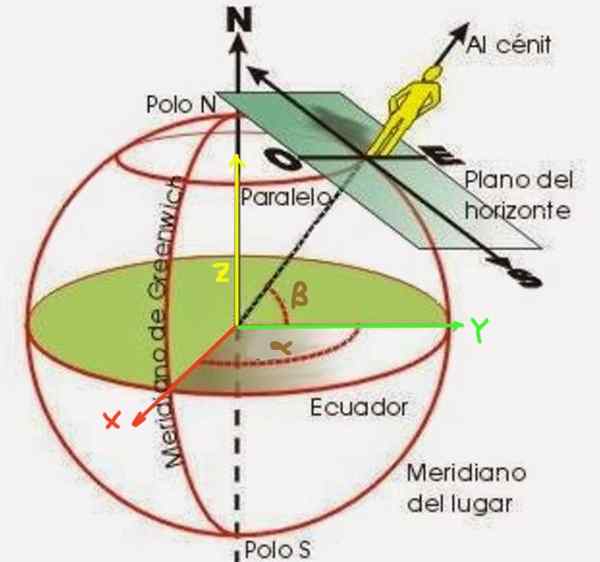figur 2. Längd a och p latitud för en observatör på jordens yta.

Ss -latitud är en vinkel som bildas av en radie som börjar från jordens centrum till den punkten att du vill positionera. Det mäts från ekvatorialplanet, som visas i figur 2. Å andra sidan är längden a vinkeln som meridianen för den punkt som placerar formen med avseende på noll meridian (känd som Greenwich Meridian).

Kan tjäna dig: relativt värde

Latitud kan vara norr eller södra latitud, beroende på om platsen som ligger ligger på norra halvklotet eller på södra halvklotet. På liknande sätt kan längden vara västerut eller detta beroende på om platsen är väster eller öster om noll meridian.

Formler för att ändra från geografiska till sfäriska

För att få dessa formler är det första att skapa ett koordinatsystem. XY -planet väljs sammanfaller med ekvatorialplanet och är den positiva semi -axeln X som går från jordens centrum och genom noll meridian. I sin tur passerar axeln och passerar genom 90º och Meridian. Jordens yta har RT -radio.

Med detta koordinatsystem är geografiska till sfäriska omvandlingar således:

αEpN → (RT, θ = 90º-p, φ = α)

αopn → (RT, θ = 90º-p, φ = 360º-a)

αP → (RT, θ = 90º+ß, φ = α)

αop → (RT, θ = 90º+β, φ = 360º-a) 

Exempel

Exempel 1

De geografiska koordinaterna för Palma de Mallorca (Spanien) är:

Östlängd 38.847º och norra latitud 39.570º. För att bestämma de sfäriska koordinaterna som motsvarar Palma de Mallorca tillämpas den första av formlerna i föregående avsnittformler:

38,847ºE39,570ºN → (r = 6371 km, θ = 90º-39,570º, φ = 38,847º)

Då är de sfäriska koordinaterna:

Palma de Mallorca: (r = 6371 km, θ = 50,43º, φ = 38,85º)

I det föregående svaret har r lika med jordens genomsnittliga radie.

Exempel 2

Att veta att Falklandsöarna (Falkland) har geografiska koordinater 59ºO 51,75ºS, bestäm motsvarande polära koordinater. Kom ihåg att x -axeln går från jordens mitt till 0 ° meridian och på ekvatorialplanet; Y -axeln också i ekvatorialplanet och genom 90º West Meridian; Slutligen Z-axeln på markens axel i syd-nord-riktningen.

Kan tjäna dig: curtos: definition, typer, formler, vad är det för till exempel

För att sedan hitta motsvarande sfäriska koordinater använder vi formlerna som presenteras i föregående avsnitt:

59ºO 51,75ºs → (r = 6371 km, θ = 90º+51,75º, φ = 360º-59º) Det vill säga

Malvinas: (r = 6371 km, θ = 141,75º, φ = 301º)

Övningar

Övning 1

Hitta de kartesiska koordinaterna för Palma de Mallorca i Cartesiano XYZ -referenssystemet som visas i figur 2.

Lösning: Tidigare erhölls i exempel 1 de sfäriska koordinaterna baserat på de geografiska koordinaterna för Palma de Mallorca. Så att formlerna som presenteras ovan kan användas för att flytta från sfäriska till kartesier:

x = 6371 km sen (50,43º) cos (38,85º)

Y = 6371 km sen (50,43º) SEN (38,85º) 

Z = 6371 km cos (50,43º)

Att utföra motsvarande beräkningar är:

Palma de Mallorca: (x = 3825 km, y = 3081 km, z = 4059)

Övning 2

Hitta de kartesiska koordinaterna på Falklandsöarna i Cartesiano XYZ -referenssystemet som visas i figur 2.

Lösning: Tidigare i exempel 2 erhölls de sfäriska koordinaterna baserat på de geografiska koordinaterna på Falklandsöarna. Så att formlerna som presenteras ovan kan användas för att flytta från sfäriska till kartesier:

x = 6371 km sen (141,75º) cos (301º)

y = 6371 km sen (141,75º) SEN (301º) 

Z = 6371 km cos (141,75º)

Att utföra motsvarande beräkningar erhålls:

Falklandsöarna: (x = 2031 km, y = -3381 km, z = -5003)

Referenser

1. Arfken g och weber h. (2012). Matematiska metoder för fysiker. En omfattande guide. Sjunde upplagan. Akademisk press. ISBN 978-0-12-384654-9
2. CC -beräkning. Löst cylindriska och sfäriska koordinatproblem. Återhämtad från: beräkning.Likström
3. Astronomi workshop. Latitud och longitud. Hämtad från: rate.Bloggfläck.com/
4. Weisstein, Eric W. ”Sfäriska koordinater.”Från Mathworld-A Wolfram Web. Återhämtat sig från: Mathworld.Volfram.com
5. Wikipedia. Sfärisk koordinatsystem. Hämtad från: i.Wikipedia.com
6. Wikipedia. Vektorfält i cylindriska och sfäriska koordinater. Hämtad från: i.Wikipedia.com