Rektangulära koordinater exempel och övningar löst

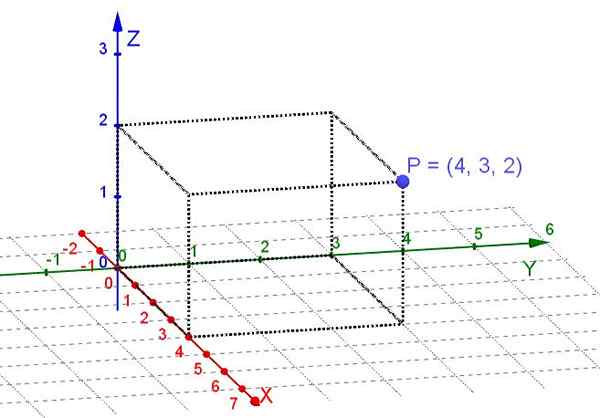
De rektangulära koordinater o Cartesian är de som erhålls när de projiceras ortogonalt på de tre kartesiska axlarna x, y, z en punkt belägen i det tre dimensionella utrymmet.

Kartesiska axlar är ömsesidigt vinkelräta orienterade raka. I det kartesiska koordinatsystemet tilldelas tre riktiga siffror som är dess rektangulära koordinater till varje punkt i rymden.

Figur 1. Rektangulära koordinater för punkt P (egen utarbetande)

Ett plan är ett underområde av tre dimensionellt utrymme. Vid övervägande av punkter på ett plan räcker det att välja ett par vinkelräta axlar x och som ett kartesiskt system. Sedan tilldelas han vid varje punkt på planet att hans rektangulära koordinater är.

[TOC]

Ursprunget till rektangulära koordinater

De rektangulära koordinaterna föreslogs ursprungligen av den franska matematikern René Descartes (1596 och 1650), varför de får valören av kartesier.

Med denna idé om Descartes tilldelas planen och rymden siffror, så att de geometriska figurerna har associerat en algebraisk ekvation och de klassiska geometriska teoremerna kan demonstreras algebraiskt. Med kartesiska koordinater föddes analytisk geometri.

Det kartesiska planet

Om två vinkelräta linjer på ett plan väljs som korsar varandra vid en punkt eller; och om varje rad tilldelas en riktning och en numerisk skala mellan successiva likvärdiga punkter, finns det då ett kartesiskt system eller en plan där varje punkt i planet är associerat med ett ordnat par av två verkliga siffror som är dess prognoser på respektive på den x och y axlar.

Poäng A = (3, 2); B = (-2, 3); C = (-2, -3) och D = (3, -3) representeras i det kartesiska planet som visas nedan:

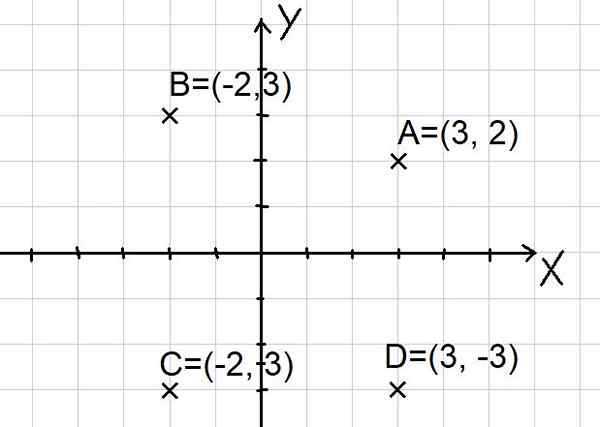figur 2. Punkter på det kartesiska planet. (Egen utarbetande)

Observera att de två x- och y -axlarna delar upp planet i fyra sektorer som kallas kvadranter. Punkt A är i den första kvadranten, B i den andra kvadranten, C i den tredje kvadranten och punkt D i den fjärde kvadranten.

Kan tjäna dig: befolkning och prov

Avstånd mellan två poäng

Avståndet mellan två punkter A och B i det kartesiska planet är längden på segmentet som förenar dem. Detta avstånd kan beräknas analytiskt enligt följande:

D (a, b) = √ (bx - ax)^2 + (av - ay)^2)

Den främre formeln erhålls genom att tillämpa Pythagoras teorem.

Att tillämpa nämnda formel på punkter a, b i figur 2 är:

D (a, b) = √ (-2 - 3)^2 + (3 - 2)^2) = √ (-5)^2 + 1^2) = √ (26)

Det vill säga att d (a, b) = 5,10 enheter. Observera att avståndet erhölls utan att behöva mäta med en regel har en helt algebraisk procedur följts.

Analytiskt uttryck för en linje

Rektangulära koordinater tillåter analytisk representation av grundläggande geometriska objekt som punkt och linje. Två punkter A och B definierar en enda linje. Linjens lutning definieras som kvoten mellan skillnaden i koordinater och punkt B mindre, dividerad av skillnaden i x -koordinaterna i punkt B mindre a:

pågående = (av - ay)/(bx - ax)

En vilken punkt med koordinater (x, y) som tillhör linjen (AB) måste ha samma lutning:

väntande = (y - ay)/(x - ax)

Ekvationen som erhålls genom jämlikheten i sluttningarna är den analytiska eller algebraiska representationen av linjen som passerar genom punkterna A och B:

(y - ay)/(x - ax) = (av - ay)/(bx - ax).

Om du tas för A och B är de rektangulära koordinaterna i figur 2:

(Y - 2)/(x - 3) = (3 - 2)/( - 2 - 3)

(y - 2)/(x - 3) = -⅕

I detta specifika fall finns det en linje med en negativ lutning -⅕, vilket innebär att det ligger på en punkt i linjen och ökar X -koordinaten i en enhet, koordinaten och minskar i 0,2 enheter. 

Kan tjäna dig: Toroid eller Toro Dona

Det vanligaste sättet att skriva ekvationen i linjen i planet är med koordinaten och tydlig som en funktion av variabel x:

y = -(1/5) x + 13/5 

Exempel

Exempel 1

Erhålla med analysmetoder avståndet mellan punkterna C och A, är de rektangulära koordinaterna för C = (-2, -3) och de för A = (3.2).

Formeln för det euklidiska avståndet mellan dessa två punkter är skriven så här:

D (a, c) = √ ((cx - ax)^2 + (cy - ay)^2)

Ersätter dess motsvarande rektangulära koordinater du har:

D (a, c) = √ (-2-3)^2 + (-3-2)^2) = √ (-5)^2 + (-5)^2) = 5√2 = 7,07

Exempel 2

Erhålla ekvationen för linjen som passerar genom punkt C för koordinater (-2, -3) och punkten P för koordinat (2, 0).

Först erhålls lutningen för CP -linjen:

pågående = (0 -(-3)) / (2 -( -2)) = ¾ 

En vilken punkt Q av generiska rektangulära koordinater (x, y) som tillhör CP -linjen måste ha samma lutning:

pågående = (y -(-3)) / (x -( -2)) = (y +3) / (x +2)

Det vill säga att ekvationen för CP -linjen är:

(Y +3) / (x +2) = ¾

Ett alternativt sätt att skriva ekvationen för CP -linjen är att rensa och:

y = ¾ x - 3/2 

Löst övningar

Övning 1

Erhålla de rektangulära koordinaterna för skärningspunkten mellan linjerna y = - (1/5) x + 13/5 och linjen y = ¾ x - 3/2.

Lösning: Per definition delar skärningspunkten för de två linjerna samma rektangulära koordinater. Därför är koordinater och vid skärningspunkten identisk för båda linjerna:

-(1/5) x + 13/5 = ¾ x - 3/2

Vad leder till följande uttryck:

Kan tjäna dig: rektangel trapezoid: egenskaper, relationer och formler, exempel

(¾ + ⅕) x = 13/5 +3/2

Att lösa summan av fraktioner erhålls:

19/20 x = 41/10

Clearing x:

x = 82/19 = 4.32

För att erhålla värdet och skärningspunkten ersätts X -värdet som erhållits i en av linjerna:

y = ¾ 4,32 - 3/2 = 1,74

Detta innebär att de givna linjerna avlyssnas vid punkt I för koordinater i = (4,32; 1,74).

Övning 2

Få omkretsekvationen som passerar genom den rektangulära koordinatpunkten R (3, 4) och som har ett centrum vid koordinaternas ursprung.

Lösning: Radio R är avståndet från punkt R till ursprung eller koordinater (0, 0).

d (r, o) = √ ((rx - 0)^2 + (ry - 0)^2) = √ ((3 - 0)^2 + (4 - 0)^2) = √ (3^2 + 4^2) = √ (9 + 16) = √ (25) = 5

Det vill säga, det är en Radius 5 Circle 5 centrerad på (0,0).

En vilken punkt P (x, y) av omkretsen måste ha samma avstånd 5 till centrum (0, 0) för vad som kan skrivas:

D (p, o) = √ ((x - 0)^2 + (y - 0)^2) = √ (x^2 + y^2) = 5

Det vill säga:

√ (x^2 + y^2) = 5

För att eliminera kvadratroten lämnas båda jämställdhetsmedlemmarna tyst:

x^2 + y^2 = 25

Vad är omkretsekvationen.

Med detta exempel illustreras kraften i det rektangulära koordinatsystemet, vilket gör det möjligt att bestämma geometriska objekt, såsom omkrets utan att behöva använda papper, penna och kompass. Den omkrets som endast begärs med algebraiska metoder har fastställts.

Referenser

1. Arfken g och weber h. (2012). Matematiska metoder för fysiker. En omfattande guide. Sjunde upplagan. Akademisk press. ISBN 978-0-12-384654-9
2. CC -beräkning. Rektangulära koordinater löste problem. Återhämtad från: beräkning.Likström
3. Weisstein, Eric W. "Kartesiska koordinater.”Från Mathworld-A Wolfram Web. Återhämtat sig från: Mathworld.Volfram.com
4. Wikipedia. Cartesian koordinatsystem. Hämtad från: i.Wikipedia.com