Enhetscirkel trigonometriska funktioner och applikationer

han Enhetlig krets Det är en radiecirkel som är lika med 1, som vanligtvis är inriktad på punkt (0,0) i det kartesiska koordinatsystemet Xy. Det används för att enkelt definiera de trigonometriska orsakerna till vinklarna med rektanglar.

Den enhetliga cirkelekvationen fokuserad på ursprung är:

x² + och² = 1

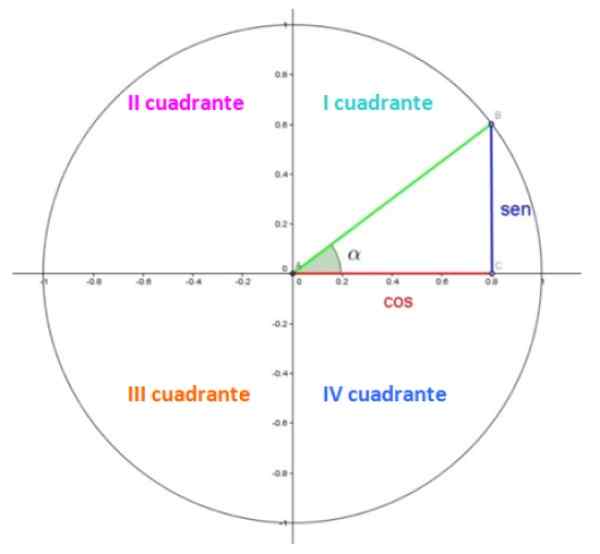
Figur 1. Enhetscirkeln. Källa: Wikimedia Commons.

I figur 1 har vi enhetscirkeln, där varje rum är i en kvadrant. Kvadranterna är numrerade med romerska siffror och räknas anti -Horary.

I den första kvadranten finns en triangel. Kategorierna i rött respektive i blått mått 0.8 och 0.6, medan hypotenusen i gröna mäter 1, eftersom det är en radio.

Den akuta vinkeln a är en central vinkel i standardläge, vilket innebär att dess toppunkt sammanfaller med punkten (0,0) och dess initiala sida med den positiva x -axeln. Vinkeln mäts i motsats till klockhänderna och genom konvention tilldelas det ett positivt tecken.

Tja, i enhetscirkeln är koordinaterna för Coseno och Sine of a respektive X- och Y -koordinaterna för punkt B, som i det visade exemplet är 0.8 och 0.6.

Från dessa två definieras de:

• TG α = sin a/cos α = 0.6/0.8 = 0.75
• SEC α = 1/ cos α = 1/0.8 = 1.25
• Skada α = 1 / sin α = 1/0.6 = 1.66 ..
• CTG α = 1/tg = 0.8/0.6 = 1.33 ..

[TOC]

Enhetscirkelapplikationer

Om vi ​​begränsar oss till rektanglar skulle trigonometriska skäl endast appliceras på akuta vinklar. Men med hjälp av enhetscirkeln utvidgas beräkningen av trigonometriska skäl till alla vinkel a.

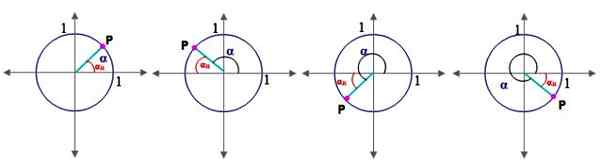figur 2.- Vinklar i kvadranterna och referensvinkeln i enhetscirkeln. Källa: f. Zapata.

För detta är det nödvändigt att definiera begreppet referensvinkel a först_R:

Kan tjäna dig: Finite Set: Egenskaper, exempel, lösta övningar

Referensvinkel

Låt α vara en vinkel i standardläge (den vars Första sammanfaller med den positiva x -axeln), dess referensvinkel a_R Det är bland dess terminal och X -axeln. Figur 2 visar referensvinkeln för vinklar i I, II, III och IV kvadrant.

För varje kvadrant beräknas referensvinkeln enligt följande:

-Första kvadranten: α_R = α

-Andra kvadrant: α_R = 180º - a

-Tredje kvadrant: α_R = α - 180º

-Fjärde kvadranten: α_R = 360º - a

Observera att den första kvadrantvinkeln a sammanfaller med sin referensvinkel. Tja, de trigonometriska orsakerna till vinkel a är desamma som deras referensvinkel, med skyltarna enligt de som har kvadranterna där terminalsidan av a faller.

Med andra ord, de trigonometriska orsakerna till att koseno och bröstet i vinkeln är sammanfaller med koordinaterna för punkt P, enligt figur 2.

I följande figur ser vi de trigonometriska orsakerna till vissa anmärkningsvärda vinklar, som härleds från enhetscirkeln.

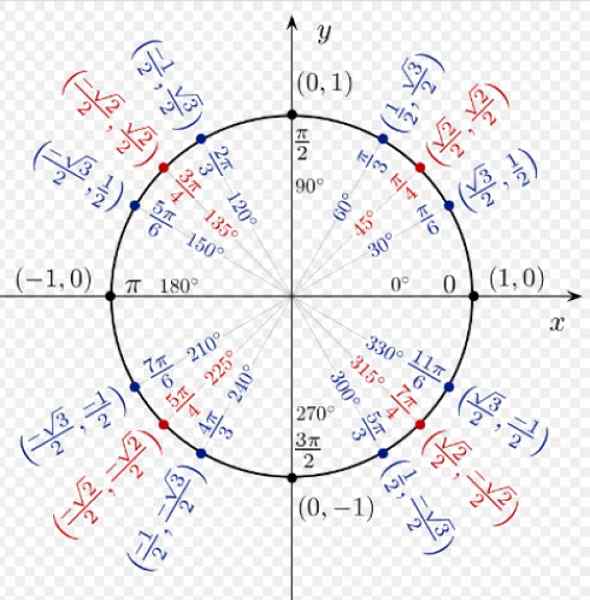Figur 3. Koordinater för några anmärkningsvärda punkter i enhetscirkeln. Källa: Wikimedia Commons.

Skälen till koseno och bröst av någon vinkel i I -kvadranten är alla positiva. För a = 60º har vi koordinaterna (1/2; √3/2), som motsvarar COS 60º och SEN 60º.

Koordinaterna för α = 120º är (-1/2; √3/2), eftersom X-koordinaten är i den andra kvadranten är negativ.

Layout av graferna för kosinus och sinus

Med hjälp av enhetscirkeln och koordinaterna för P -punkterna på den är det möjligt att rita graferna för funktionerna cos t och sen t, som vi kommer att se nedan.

Kan tjäna dig: vinkelförskjutning

För detta finns flera positioner för punkt P (t) i enhetscirkeln. Vi börjar med grafen för funktionen f (t) = sen t.

Vi kan observera att när vi går från t = 0 till t = π/2 (90º) ökar värdet på sen t till 1, vilket är det maximala värdet.

Å andra sidan, från t = π/2 till t = 3π/2 Sinens värde minskar från 1 och passerar genom 0 vid t = π till dess minimum -1 vid t = 3π/2.

Figuren visar grafen för den första cykeln av f (t) = sen t som motsvarar den första återgång till enhetscirkeln, denna funktion är periodisk period 2π.

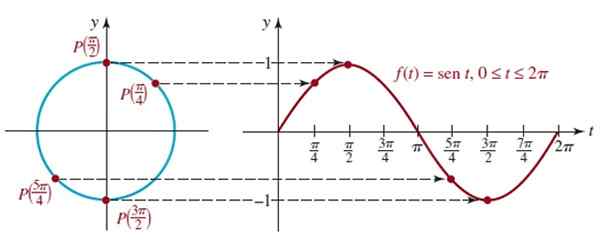Figur 4. Figuren av grafen för f (t) = sen t för en cykel. Källa: Zill, D. Algebra, trigonometri och analytisk geometri.

En analog procedur kan utföras för att erhålla grafen för funktionen f (t) = cos t, som visas i följande animation:

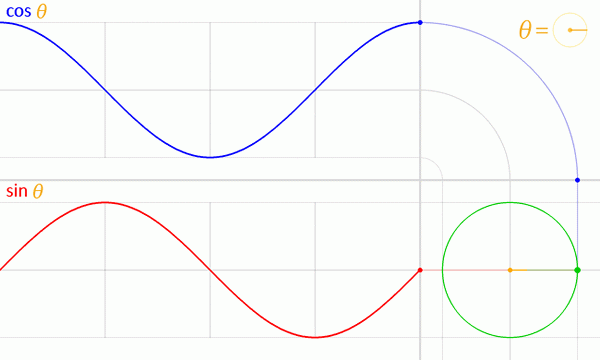Figur 5. Grafer över sinus- och kosinusfunktionerna från enhetscirkeln. Källa: Wikimedia Commons.

Seno och Coseno funktioner egenskaper

-Båda funktionerna är kontinuerliga i uppsättningen av verkliga och periodiska siffror, av period 2π.

-Domänen för funktioner f (t) = sen t och f (t) = cos t är alla verkliga siffror: (-∞, ∞).

-För bröst- eller sinus- och kosinusvägen har du intervallet [-1,1]. Konsolerna indikerar att -1 och 1 ingår.

- Sin t -nollorna är värdena som motsvarar nπ med n heltal, medan nollorna för cos t är [(2n+1)/2] med n också helhet.

-Funktionen f (t) = sin t är udda, har symmetri med avseende på ursprunget medan cos t -funktionen är jämn, dess symmetri är med avseende på den vertikala axeln.

Kan tjäna dig: slumpmässiga val med eller utan ersättning

Löst övningar

- Övning 1

Givet cos t = - 2/5, som är den horisontella koordinaten för punkt P (t) i enhetscirkeln i den andra kvadranten, erhåller motsvarande vertikala koordinat SEN T.

Lösning

Eftersom p (t) tillhör enhetscirkeln, där det uppfylls det:

x² + och² = 1

Därför:

y = ± √ 1 - x²

Eftersom p (t) är i den andra kvadranten kommer det positiva värdet att tas. Den vertikala koordinaten för punkt P (t) är y:

y = √ 1 - (-2/5)² = √0.84

- Övning 2

En matematisk modell för temperatur T I grader Fahrenheit på vilken dag som helst, t Timmar efter midnatt ges det av:

T (t) = 50 + 10 sen [(π /12) × (t - 8)]

Med T förstås mellan 0 och 24 timmar. Hitta:

a) Temperaturen klockan 8.

b) timmar under vilka t (t) = 60 ºF

c) Maximala och minimala temperaturer.

Lösning till

Vi ersätter t = 8 i den givna funktionen:

T (8) = 50 + 10 sen [(π/12) × (t-8)] = 50 + 10 sen [(π/12) × (8-8)] =

= 50 + 10 x sen 0 = 50 ºF

Lösning B

50 + 10 sen [(π/12) × (T-8)] = 60

Det är en trigonometrisk ekvation och du måste rensa det okända "T":

10 sen [(π/12) × (t -8)] = 60 - 50 = 10

sin [(π/12) × (t-8)] = 1

Vi vet att sen π/2 = 1, därför måste bröstargumentet vara 1:

(π/12) × (t-8) = π/2

T-8 = 6

t = 14 timmar

Det dras slutsatsen att 14 timmar efter midnatt är temperaturen 60 °, det vill säga kl. 14.00. Det finns ingen annan timme under dagen (24 timmar) där detta händer.

Lösning C

Den maximala temperaturen motsvarar värdet i vilket SEN [(π/12) × (t-8)] = 1 och är 60 ºF. Å andra sidan inträffar minsta om SEN [(π/12) × (t -8)] = -1 och är 40 ºF.

Referenser

1. Figuera, J. 1999. Matematik. Första. Diversifierad. Bolivariska kollegiala utgåvor.
2. Hoffman, J. Urval av matematikfrågor. Volym 4.
3. Jiménez, r. 2008. Algebra. Prentice hall.
4. Matematik är kul. Enhetscirkel. Återhämtat sig från: från: Mathsisfun.com.
5. Wikipedia. Trigonometri -identiteter och formler. Återhämtad från: är.Wikipedia.org.
6. Zill, D. 1984. Algebra och trigonometri. McGraw Hill.