Trigonometriska identiteter (exempel och övningar)

De trigonometriska identiteter Dessa är förhållanden mellan trigonometriska skäl, som är sanna för alla variabelvärden. Till exempel:

Solbränna θ = sin θ /cos θ

Det är en trigonometrisk identitet som relaterar tre orsaker till vinkeln θ, tangenten, bröstet och kosinusen i nämnda vinkel.

Figur 1. Vissa trigonometriska identiteter som används allmänt vid beräkning. Källa: f. Zapata.

Denna identitet gäller för allt värde, utom de som gör 0 nämnaren. Cos θ är 0 för θ = ± π/2, ± 3π/2, ± 5π/2 ... Ett annat exempel på trigonometrisk identitet är:

synd x . Sec x . CTG x = 1

[TOC]

Demonstration

Det finns två grundläggande sätt att visa att en trigonometrisk identitet är sant:

1- Omvandla en av medlemmarna i jämlikhet till den andra, genom praktiska algebraiska manipulationer.

2- Utveckla båda jämställdhetsmedlemmarna separat, tills respektive slutliga uttryck för var och en är exakt samma.

I den föreslagna identiteten kommer vi att förvandla den vänstra sidan av jämlikhet, för vilken vi uttrycker CTG X och Sec X när det gäller bröst och kosinus enligt följande:

Ctg x = cos x / sen x

Sec x = 1 /cos x

Vi ersätter detta uttryck på vänster sida av identiteten och förenklar:

synd x . (1/cos x). (cos x / sen x) = (sin x. cos x / cos x . sin x) = 1

Och identitetens sanningsenhet är redan bevisat.

Typer av trigonometriska identiteter

Det finns flera typer av trigonometriska identiteter. Därefter kommer vi kort att beskriva de viktigaste:

- Grundläggande trigonometriska identiteter

Vi skiljer två typer av grundläggande identiteter:

I) de som uttrycks genom de grundläggande orsakerna, kosinus och tangent:

• Sec x = 1 /cos x
• Skada x / 1 / sin x
• Ctg x = 1 / tg x
• Tg x = sin x /cos x
• Ctg x = cos x / sen x

I) de som härrör från paritet. Vi vet genom dess graf att Sen X är en udda funktion, vilket innebär att:

Kan tjäna dig: 60 delare

sin (-x) = - synd x

För sin del är Cos X därför ett par:

cos (-x) = cos x

Så:

tg (-x) = sen (-x) / cos (-x) = -sen x / cos x

Liknande:

• cotg (-x) = -ctg x
• sec (-x) = sek x
• skada (-x) = - skada x

- Pythagorean identitet

Det är de som erhålls från tillämpningen av Pythagoras teorem till rektangelns triangel av katter A och B och Hypotenusa C. Låt oss se:

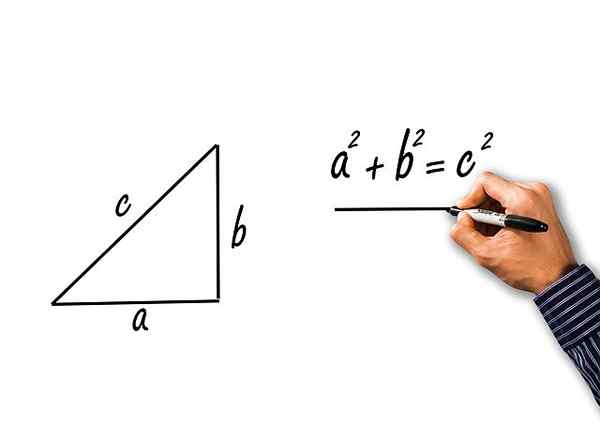figur 2.- Från Pythagoras teorem erhålls de tre Pythagorean trigonometriska identiteterna. Källa: Pixabay.

Pythagoras sats säger att:

c² = a² + b²

Dela allt mellan C²:

c² / c² = (a² / c²) + (B² / c²)

Termen till vänster är 1 och kommer ihåg att sinus och kosinus i den akuta vinkeln a definieras som:

sin α = a/c

cos α = b/c

Resultat:

1 = (sin α)² + (cos α)²

Denna identitet kallas grundläggande identitet.

Proceduren kan utföras genom att dela mellan² och b², vilket ger upphov till ytterligare två identiteter:

Sekund² α = 1 + TG² a

ham² α = 1 + CTG² a

- Formler för kosinus och bröstet för summan/subtraktionen av vinklar

De viktigaste trigonometriska identiteterna för kosinus, bröst och tangent av summan och subtraktionen är följande:

SEN -demonstration (α + β) och COS (α + ß)

Dessa identiteter kan demonstreras geometriskt eller även genom Euler -formeln:

och^Ia = cos α + i sin α

Låt oss titta på vad som händer med formeln när du ersätter summan av två vinklar α och ß:

och^{I (α +p)} = cos (α + ß) + i sin (α + ß)

Detta uttryck är komplex, dess verkliga del är cos (α + ß) och dess imaginära del är I Sin (α + ß). Vi håller detta resultat att använda det senare och fokusera på att utveckla den exponentiella delen:

och^{I (α +p)} = e^Ia ⋅ E^iβ = (cos a + i sin α) . (cos ß + i sin β) =

Kan tjäna dig: hexagonalt prisma

= COS α⋅COS ß + COS α⋅I SEN ß + I⋅SEN α ​​COS ß - SEN α⋅SEN ß

Den verkliga delen av detta uttryck är det som inte multipliceras med den imaginära enheten "I":

COS α⋅COS ß - SEN α. Sen β

Den imaginära delen är därför:

I (COS α⋅SEN ß + SEN α⋅COS β)

För att två komplexa uttryck ska vara desamma måste den verkliga delen av den ena vara lika med den verkliga delen av den andra. Detsamma gäller för imaginära delar.

Vi tar resultatet sparat och jämför det med detta:

cos a. cos ß - SEN α. Sin β = cos (α + β)

I (COS α⋅SEN ß + SEN α⋅COS ß) = I SIN (α + β)

SIN (α + β) = (COS a. Sin ß + SEN α⋅COS β)

- Formler för dubbelvinkeln

I de föregående formlerna tar vi β = α och utvecklar:

SIN (α + α) = SEN 2 α = SEN α⋅COS a + cos a. sin α = 2⋅ sin α ⋅ cos a

COS (α + α) = cos 2 a = cos α⋅COS a - SEN α⋅SEN α ​​= cos² α - SEN ² a

Tg (α + α) = Tg 2 a = [Tg a + Tg α] / [1- Tg a⋅tg α] = 2TG a / 1- TG² a

Om i det andra uttrycket cos ersätts² α = 1 - SEN² a erhålls:

cos 2 α = cos² a- (1- cos² α) = 2 cos² α -1

- Halvhangelformler

I det sista uttrycket ersätter vi a med a/2, följande kvarstår:

cos α = 2 cos ²(α/2) -1

Clearing:

Löst övningar

- Övning 1

Visa det:

Lösning

Vi kommer att arbeta algebraiskt termen vänster så att det ser ut som rätt. Som på rätt sikt visas sen x, är det första steget att uttrycka cos²X när det gäller sen x så att allt är i termer av samma trigonometriska skäl:

Det kan tjäna dig: fraktion motsvarande 3/5 (lösning och förklaring)

Då är 1 - Sen faktor² X för att vara en skillnad av perfekta rutor. För att göra detta rensar det från den grundläggande identiteten:

cos²X = 1 - sen² x

1 - Sen² x = (1- sin x) (1+SENX)

Och faktoriseringen i det ursprungliga uttrycket ersätts:

Termen (1- SENX) förenklas och en jämlikhet kvarstår:

1 + SEN x = 1 + SENX

- Övning 2

Lös följande trigonometrisk ekvation och ge lösningen för värden mellan 0 och 360º:

Tg x + sek² x = 3

Lösning

Under vänsterperioden finns det två trigonometriska skäl, därför måste du minska allt till ett för att kunna rensa det okända. Termen SEC² X uttrycks genom en av de pytagoreiska identiteterna:

Sekund² α = 1 + TG² a

Genom att ersätta ekvationen:

Tg x + 1 + tg² x = 3

Omarrangera villkoren:

Tg² x + tg x + 1 = 3

Denna ekvation löses genom att ändra variabeln:

tg x = u

eller² + U + 1 - 3 = 0 → U² + U - 2 = 0

Denna andra gradsekvation löses enkelt genom faktorisering:

(U +2) (U-1) = 0

Därför u₁ = -2 och u₂ = 1, motsvarande:

Tg x₁ = -2

Tg x₂ = 1

Till sist:

x₁ = arctg (-2) = 296.Sjätte

x₂  = arctg (1) = 45º

Referenser

1. Carena, m. 2019. Matematikhandbok för preuniversitet. National University of the Coast.
2. Figuera, J. 1999. Matematik. Första. Diversifierad. Bolivariska kollegiala utgåvor.
3. Hoffman, J. Urval av matematikfrågor. Volym 4.
4. Jiménez, r. 2008. Algebra. Prentice hall.
5. Wikipedia. Trigonometri -identiteter och formler. Återhämtad från: är.Wikipedia.org.
6. Zapata, f. 4 sätt att lösa en andra gradsekvation. Återhämtat sig från: FrancesPhysics.Bloggfläck.com.
7. Zill, D. 1984. Algebra och trigonometri. McGraw Hill.