Historik om bakgrund och utvecklingsgeometri från dess ursprung

De Geometrihistoria Det börjar med de första civilisationerna som använde sig av denna gren av matematik på ett praktiskt sätt, särskilt folken i Indo Valley och Babylon som kände till de stötta trianglarna, cirka 3000 till.C.

I skrifterna av den egyptiska skrivaren Ahmes (1550 till.C.) Metoder används för att beräkna området för en cirkel. För sin del hade babylonierna allmänna regler för att mäta volymer och områden. 

Ahme Papyrus eller Rhind Mathematical Papyrus

Båda civilisationerna, egyptierna och babylonierna, kände versioner av Pythagoras teorem 1500 år före Pythagorean -versionerna. Å andra sidan indianerna från den vediska perioden (1500-100 till.C.) använde geometri i altare konstruktion.

[TOC]

Antikens Grekland

Grekarna var benägna mot utvecklingen av matematik under lång tid. Karaktärer som Pythagoras och Platon, relaterade till siffror med allt som finns i världen. För dem var matematik nyckeln till att tolka universum; Detta ideal följde i följarna av Pythagoreans i flera århundraden.

Tales of Miletus

Tales de Mileto var en av de första grekerna som bidrog till framstegen med geometri. En lång tid tillbringad i Egypten och från dessa lärda grundläggande kunskaper. Han var den första som etablerade geometri -mätformler.

Tales of Miletus

Han lyckades mäta höjden på Pyramiderna i Egypten och mätte sin skugga i det exakta ögonblicket där dess höjd var lika med måtten på dess skugga.

Pythagoras

Pythagoras

Inom det viktigaste bidraget från Pythagoras (569 till.C. - 475 a.C.Till geometrien är det berömda teoremet för Pythagoras, som fastställer att inom en rektangel triangel är hypotenusens kvadrat (den sida som motsätter sig rätt vinkel) lika med summan av de återstående sidorna.

Element av euklid

Det mest framträdande arbetet som har räddats sedan forntiden har varit studien Elementen, från Euclid de Alejandría (325 a.C. - 265 a.C.), gjord under 300 -talet till.C. Det är ett verk med stort historiskt värde som har fungerat som grund för undervisningen i matematik i mer än 2000 år.

Euklid

Elementen Det var en av de första böckerna och sammanställningar av studier som förklarade matematiska principer som kunde tillämpas på alla situationer. Inkluderar postulater, som är de grundläggande principerna för geometri i deras arbete. Å andra sidan finns det de kvantitativa principerna som kallas de grundläggande uppfattningarna.

Euklidundervisning reducerade konstruktionsinstrument inom geometri till endast två: en regel utan åtgärder och en kompass. Detta genererade de tre klassiska problemen som inte hittade svar förrän 1800 -talet: cirkelns kvadratur, duplicering av kuben och trisection of a vinkel. 

Kan tjäna dig: i vilket århundradet erövrade tenochtitlán?

För de gamla var de två idealiska geometriska enheterna den raka linjen och cirkeln, så de flesta geometriska teorier som föreslogs var produkten av utforskning med dessa instrument.

Geometri i astronomi

Geometrien gynnades också för grekerna när det gäller studien av stjärnorna. De beräknade rörelserna genom observationen och gjorde geometriska plan på himlen och etablerade jorden som en central punkt, och både solen och månen och de andra planeterna och enheterna som rörde sig runt dem och roterade i en uppsättning cirklar. 

Ett av de mest inflytelserika bidragen var Almagest, skriven under andra århundradet d.C av Claudio Ptolemy (100 d. C.- 170 d.C), en astronomisk fördragsbehållare av stjärnkatalogen. Det var den mest fullständiga texten i hans tid och påverkade astronomiska studier på ett transcendentalt sätt tills medeltiden mycket avancerade. Det var en del av media som mest populariserade det geocentriska systemet, som hävdade att jorden var universums centrum.

Ptolemi

Islamiskt inflytande

Mot IX -århundradena, när den arabiska världen var i sin stora expansion, genomsyrade mycket av dess kultur flera vetenskapsområden och konst. De var stora fans av grekernas matematiska och filosofiska verk. 

En av de mest utforskade grenarna inom deras behov var astronomi för att hitta den exakta orienteringen där MECA skulle utföra meningarna.

Efter studierna av Euclid och andra bidrag som Ptolemaios, utvecklade muslimer den stereografiska projektionen, det vill säga projektionen av himmelsfären i planet för att använda den som en karta. Detta innebar framsteg när det gäller studien av trigonometri.

Bland de mest representativa karaktärerna är Thābit ibn Qurra (826/36-901) som gjorde relevanta översättningar av de forntida texterna Apollonius, Archimedes, Euclid och Ptolemy. Några av dessa är de enda överlevande versionerna av forntida skrifter.

Utforskningarna angående astronomisk geometri tillät också skapandet av ett av de mest representativa instrumenten, Astrolabio, som förenklade de astronomiska beräkningarna för ögonblicket. Dessutom tillät detta instrument dem också att veta tid och slutligen få vägledning till MECA. 

Det kan tjäna dig: 8 seder och traditioner för blandningen

Europeisk arvutveckling

Under det tolfte århundradet, efter införandet av grekernas klassiska läror tack vare den muslimska expansionen och utvecklingen av samma upptäckter, började översättningar av latinska texter direkt från grekiska att göras direkt från det grekiska eller från arabiska språket. 

Detta skulle ge plats för ett nytt lärande inom Europa som skulle främjas av renässansen. Återupptäckten av föreställningar som "bevisen" började, ett koncept utvecklades bland grekerna som var intresserade av demonstrationen av postulaten i verkligheten.

Geometri i konst

Kunskap återspeglades också i konsten, såsom målning eller arkitektur, eftersom geometri skulle börja vara en grundläggande del av utvecklingen av perspektiv inom konst.

Filippo Brunelleschi (1377-1446) var den som lyckades utveckla det linjära perspektivet genom matematik. Syftet med denna teori var att i ett plan representerar ett tre -dimensionellt utrymme från hur det uppfattades av det mänskliga ögat. Således fastställer den att alla linjer i en bild var tvungen att konvergera eller hitta ett läckage för att generera djupet av djupet. 

Filippo Brunelleschi. Källa: I, Sailko/CC BY-S (http: // CreativeCommons.Org/licenser/BY-SA/3.0/)

Brunelleschi var den första som beskrev perspektivet som ett vetenskapligt förfarande och detta fungerade som grund för efterföljande jobb inom konsten.

Inom andra exempel på tillämpning av geometri på studien av konst och människan i sig är Leonardo da Vinci (1452 -1519) i sin ritning Vitruvio man. Det är en studie baserad på de mest perfekta proportionerna för människokroppen genom en geometrisk analys av dess struktur.

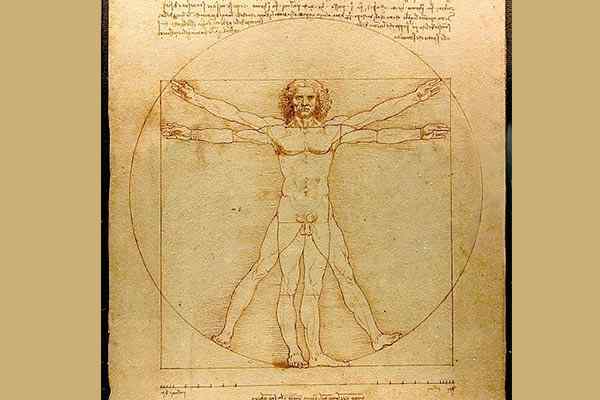The Man of Showcase av Leonardo da Vinci / Public Domain

Bland andra områden sticker arkitekturen också ut, där olika element som symmetri och balans började framträda som grundläggande egenskaper. Fyrkantiga, rektangulära dörrar och fönster, placerade på ett balanserat sätt; Användning av klassiska element i antiken som kolumner, kupoler och valv.

Steg till moderniteten

Analysen av perspektiv och prognoser under renässansen var ett av incitamenten för att väcka matematikernas intresse. Från detta ögonblick börjar mer solida och komplexa matematiska baser grundas inom geometri.

Ett av de viktigaste verken för moderniteten var arkitekten Girard avväpnad (1591-1661), som antog början för projektiv geometri. Å ena sidan konstaterade det att de parallella linjerna i en projektion bör konvergera vid en punkt på Infinity -linjen, det vill säga horisonten.

Kan tjäna dig: Tuxtepec -uppror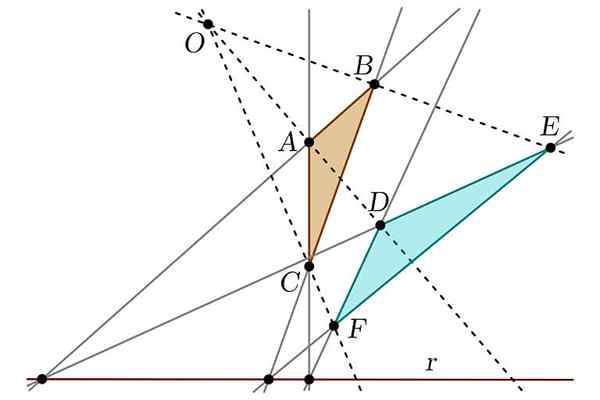Avstänga

Å andra sidan upptäckte han också vad som skulle erkännas som orolighetsteoremet, som fastställer förhållandet mellan två figurer som kan betraktas som "projektiva". Det var också ansvarigt för att förenkla Apollonius verk med avseende på avsnitten av en kon, vilket gjorde analogier mellan denna figur och cylindern.

En annan stor händelse under perioden var skapandet av analytisk geometri genom studier av René Descartes (1596-1650) och Pierre de Fermat (1601-1665) oberoende. Detta är studien av geometri genom användning av ett koordinatsystem. 

René Descartes som arbetar på ditt skrivbord. Wikimedia Commons

Icke -euklidisk geometri

Mot 1700- och 1800 -talet började studierna i icke -euklidisk geometri. Specifikt var Gauss, Johann Boleai och Lobachevsky, som fann att det femte postulatet av Euclid, känd som parallell postulat, inte kunde verifieras.

På detta sätt utvecklade de en typ av geometri där detta postulat var kvalificerat som falskt. Denna nya form lyckades genom att ge tillfredsställande resultat i geometri -stilar som inte nödvändigtvis mötte alla euklidpostulat. Således föddes hyperbolisk geometri och elliptisk geometri senare.

Det är värt att lyfta fram arbetet med Leonhard Euler (1707-1783) på 1700-talet, med avseende på utvecklingen av matematisk notation. Därefter skulle det tjugonde århundradet medföra utvecklingen av mer specifika områden med geometri bland vilka är:

-Algebraisk geometri: Det är en gren av matematik som kombinerar abstrakt algebra och analytisk geometri.

-Ändlig geometri: Det är ett geometriskt system som består av en begränsad mängd punkter, det vill säga de har ett slut eller gräns och därför kan de mätas.

-Digital geometri: Det är en gren av datavetenskap att studien av algoritmer och datastrukturer som kan representeras i geometriska termer. 

Referenser

1. (2016) Vad gjorde Euclid Elements till den enda boken som kan tävla med Bibeln. Bbc. BBC återhämtade sig.com
2. De tre klassiska problemen med grekisk matematik. University of Antioquia. Återhämtat sig från undervisningen.du.Edu.co
3. Heilbron J.L (2020). Geometri. Encyclopædia Britannica. Återhämtat sig från Britannica.com
4. Geometrihistoria. Wikipedia, den fria encyklopedin. Hämtas från.Wikipedia.org
5. Analytisk geometri. Wikipedia, den fria encyklopedin. Hämtas från.Wikipedia.org
6. (2017) Geometri och matematik i renässansen. Återhämtat sig från ukessays.com
7. Sáiz a. Linjärt perspektiv i Brunelleschi. University of Valencia. UV återhämtat sig.är
8. Redaktörerna för Encyclopaedia Britannica (2019). Renässansarkitektur. Encyclopædia Britannica. Återhämtat sig från Britannica.com
9. Andersen K (2020). Girard avväpnad. Encyclopædia Britannica. Återhämtat sig från Britannica.com
10. (2011) En intressant introduktion till beräkningsgeometri. Hämtad från Gaussians.com