Fyrkantiga element, egenskaper, klassificering, exempel

En fyrsidig Det är en fyrsidig polygon och fyra vertikaler. Deras motsatta sidor De är de som inte har några vanliga vertikaler, medan de är det på varandra följande sidor De som har ett gemensamt toppunkt.

I en fyrkantig är de angränsande vinklar De som delar en sida, medan Motsatt vinklar De har inga vanliga sidor. En annan viktig egenskap hos en fyrkantig är att summan av dess fyra Inre vinklar Det är dubbelt så mycket som den platta vinkeln, det vill säga 360 ° eller 2π radianer.

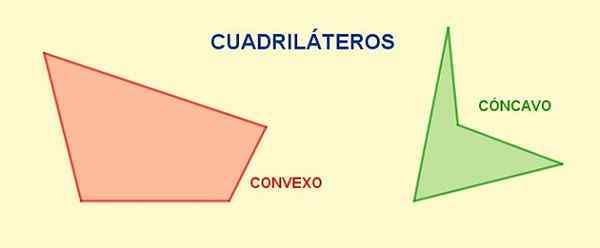
Figur 1. Olika fyrkantiga. Källa: f. Zapata.

Diagonalerna De är de segment som förenar ett toppunkt med motsatsen och i en given ring, från varje toppunkt kan du rita en enda diagonal. Det totala antalet diagonaler i en fyrkant är två.

Quadrilaterals är figurer som är kända för mänskligheten sedan forntiden. Arkeologiska poster, liksom de konstruktioner som överlever idag, vittnar om det.

Också idag fortsätter kvadrilatererna att ha en viktig närvaro i det dagliga livet. Läsaren kan hitta detta formulär på skärmen som texten läser i detta exakta ögonblick, i fönstren, dörrarna, bildelarna och otaliga platser mer.

[TOC]

Klassificering av fyrkantiga

Enligt parallellen på motsatta sidor klassificeras kvadrilateralerna enligt följande:

1. Trapezoid, När det inte finns någon parallellitet och fyrkant är konvex.
2. Trapets, När det finns parallellitet mellan ett enda par motsatta sidor.
3. Parallellogram, När deras motsatta sidor är parallella två till två.

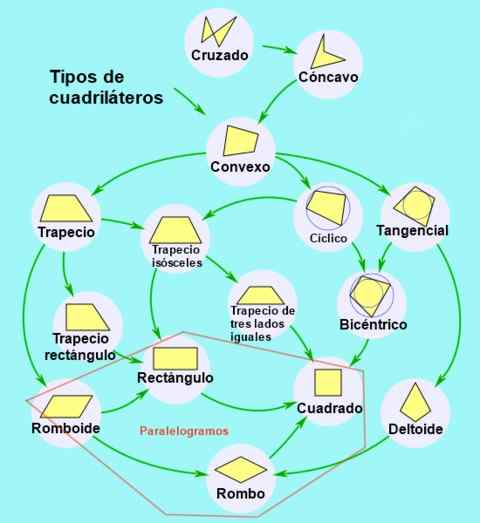figur 2. Klassificering och underklassificering av fyrkantiga. Källa: Wikimedia Commons.

Typer av parallellogram

I sin tur kan parallellogram klassificeras enligt deras vinklar och sidor enligt följande:

1. Rektangel, Det är parallellogrammet som har sina fyra inre vinklar med lika mått. De inre vinklarna på en rektangel bildar en rätt vinkel (90º).
2. Fyrkant, Det är en rektangel med sina fyra sidor av lika mått.
3. Diamant, Det är parallellogrammet med sina fyra sidor, men dess olika angränsande vinklar.
4. Romboid, parallellogram med olika angränsande vinklar.

Trapets

Trapeze är en konvex fyrkant med två parallella sidor.

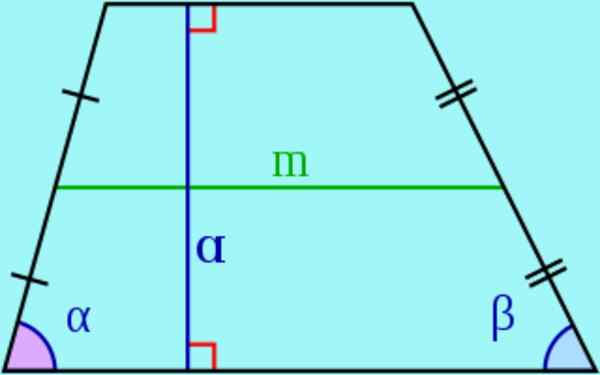Figur 3. Baser, lateral, höjd och median av en trapes. Källa: Wikimedia Commons.

- I en trapes kallas de parallella sidorna baser Och de icke -parallellerna kallas lateral.

- De höjd av en trapes är avståndet mellan de två baserna, det vill säga längden på ett segment med ändar i baserna och vinkelrätt till samma. Detta segment kallas också en trapeshöjd.

- De median Det är segmentet som ansluter sig till sidorna på sidorna. Det kan demonstreras att medianen är parallell med trapesbaserna och dess längd är lika med basens halvkroppar.

- Området för en trapes är dess höjd multiplicerad med basens halvkroppar:

Area of ​​a Trapeze = höjd * (bas 1 + bas 2) / 2

Typer av trapes

-Rektangel trapes: Det är den som har en sida vinkelrätt mot baserna. Denna sida är också höjden på trapezoiden.

-Trapeziumsosceler: Den med samma längd sidor. I en isosceles trapezoid är vinklarna intill baserna lika.

-Trapesio: Den som har sina sidor av annan längd. Dess motsatta vinklar kan vara akuta och den andra stöt, men det kan också hända att båda är stöt eller båda akuta.

Kan tjäna dig: Löst faktoriseringsövningar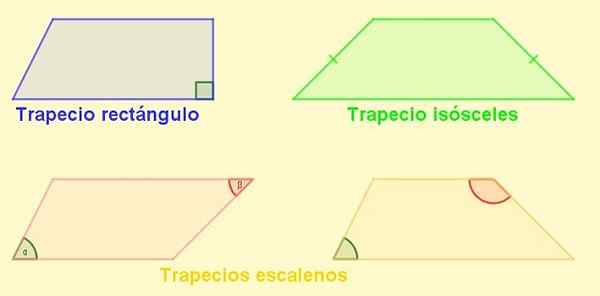 Figur 4. Typer av trapes. Källa: f. Zapata.

Parallellogram

Parallellogrammet är en fyrkantig vars motsatta sidor är parallella med två. I ett parallellogram är de motsatta vinklarna desamma och de angränsande vinklarna är kompletterande, eller med andra ord, de angränsande vinklarna totalt 180º.

Om ett parallellogram har en rätt vinkel, kommer alla andra vinklar också att vara och den resulterande figuren kallas rektangel. Men om rektangeln också har sina angränsande sidor av samma längd, är alla dess sidor lika och den resulterande figuren är en fyrkant.

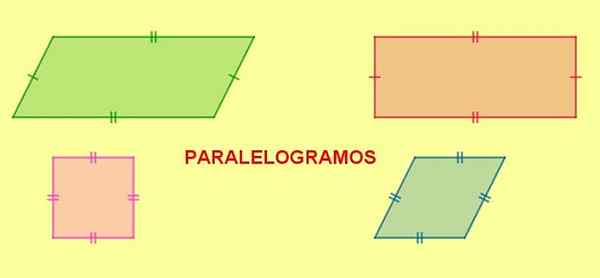Figur 5. Parallellogram. Rektangeln, torget och romb är parallellogram. Källa: f. Zapata.

När ett parallellogram har två angränsande sidor av samma längd kommer alla sidor att vara av samma längd och den resulterande figuren är en diamant.

Höjden på ett parallellogram är ett segment med ändar på dess motsatta sidor och vinkelrätt mot dem.

Ett parallellogram område

Området för ett parallellogram är produkten av basen efter dess höjd, basen är en sida vinkelrätt mot höjden (figur 6).

Område för ett parallellogram = bas x höjd = a . h

Diagonaler i ett parallellogram

Kvadratet på diagonalen som startar från ett toppunkt är lika med summan av rutorna på de två sidorna intill nämnda toppunkt mer den dubbla produkten från dessa sidor med kosinusen i vinkeln i det toppunktet:

F² = a² +  d² + 2 a d cos (α)

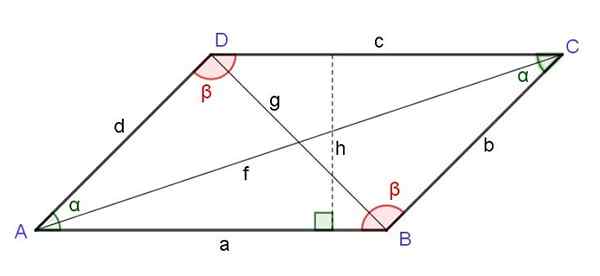Figur 6. Parallellogram. Motsatta vinklar, höjd, diagonaler. Källa: f. Zapata.

Kvadratet för det diagonala som motsätter sig toppen av ett parallellogram är lika med summan av kvadrarna på de två sidorna intill nämnda toppunkt och subtraherade den dubbla produkten av dessa sidor med kosinusen i vinkeln i den toppunkten:

g² = a² + d² - 2 a d cos (α)

Parallellogramlag

I alla parallellogram är summan av torgarna på deras sidor lika med summan av kvadrarna i diagonalerna:

till² + b² + c² + d² = f² + g²

Rectangangle

Rektangeln är en fyrkantig med dess motsatta sidor parallella med två och som också har en rätt vinkel. Det vill säga att rektangeln är en typ av parallellogram med rätt vinkel. För att vara parallellogram, Rektangeln har sina motsatta sidor av samma längd a = c och b = d. 

Men som i alla parallellogram angränsande vinklar är kompletterande och de lika motsatta vinklarna, i rektangeln genom att ha rätt vinkel, kommer den nödvändigtvis att bilda raka vinklar i de andra tre vinklarna. Det vill säga I en rektangel mäter alla inre vinklar 90º eller π/2 radianer.

Diagonaler i en rektangel

I en rektangel är diagonalerna lika längd, Som kommer att visas nedan. Resonemanget är som följer; En rektangel är ett parallellogram med alla raka vinklar och det är därför det ärver alla parallellogramets egenskaper, inklusive formeln som ger längden på diagonalerna:

F² = a²+  d² + 2 a d cos (α)

g² = a² + d² - 2 a d cos (α)

med α = 90º

Som Cos (90º) = 0, Så det händer att:

F² = g² = a² +  d²

Det är f = g, och därför längderna F och g Av de två diagonalerna i rektangeln är de lika och deras längd ges av:

Diagonal längd på en rektangel = √ (a² + b²)

Dessutom, om det är i en rektangel av angränsande sidor till och b Den ena sidan är baserad på den andra sidan kommer att vara höjd och följaktligen kommer rektangelområdet att vara:

Det kan tjäna dig: Fibonacci Series: Egenskaper, naturliga relationer, applikationer

Rektangelområde = a x b.

Omkretsen är summan av alla sidor av rektangeln, men eftersom motsatserna är desamma är det då nödvändigt för en sidorektangel till och b Omkretsen ges av följande formel:

Rektangel omkrets = 2 (a + b)

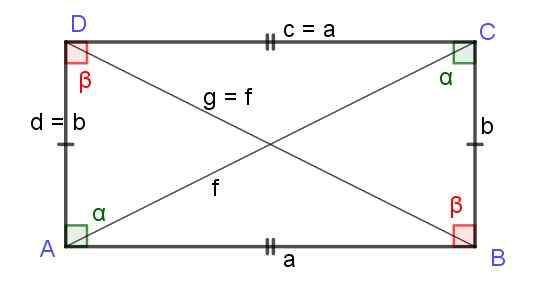Figur 7. Rektangel av sidor a och b. Diagonalerna F och G är lika längd. Källa: f. Zapata.

Fyrkant

Torget är en rektangel med dess intilliggande sidor av samma längd. Om torget har sida till, Sedan hans diagonaler F och g De har samma längd, vilket är F = g = (√2) a.

Området på en torg är dess sida upphöjd till torget:

Area på en fyrkant = a²

Omkretsen av en fyrkant är dubbelt så stor som:

Omkrets av en kvadrat = 4 a

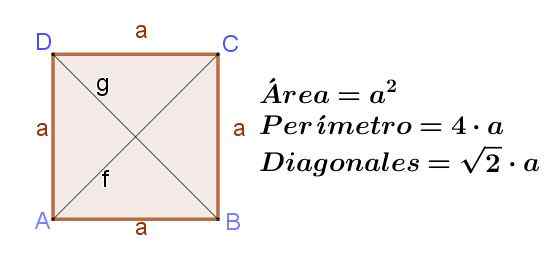Figur 8. Kvadrat till sida a, vilket indikerar dess område, dess omkrets och längden på dess diagonaler. Källa: f. Zapata ..

Diamant

Rhombus är ett parallellogram med dess intilliggande sidor av samma längd, men som i ett parallellogram är de motsatta sidorna desamma då, Alla sidor av en romb är lika lång.

Diagonalerna i en romb är av annan längd, men de skärs i rät vinkel.

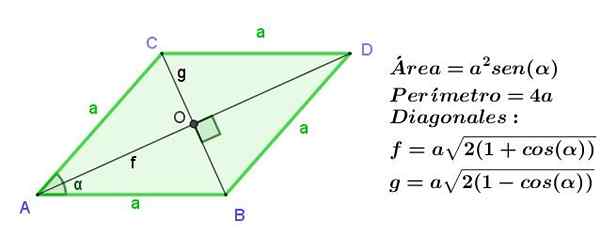Figur 9. Rhombus från sida A, vilket indikerar dess område, omkrets och längden på dess diagonaler. Källa: f. Zapata.

Exempel

Exempel 1

Visa att i en fyrkantig (inte korsad) totalt de inre vinklarna totalt 360º.

Figur 10: Det visas som summan av vinklarna på en fyrkantig tillägg 360º. Källa: f. Zapata.

ABCD anses vara en ABCD (se figur 10) och den diagonala BD dras. Två ABD- och BCD -trianglar bildas. Summan av de inre vinklarna i ABD -triangeln är:

α + β₁ + Δ₁ = 180º

Och summan av de inre vinklarna i BCD -triangeln är:

 ß2 + y + Δ₂ = 180º

Att lägga till de två ekvationerna erhålls:

α + β₁ + Δ₁ +  p₂ + y + Δ₂ = 180º + 180º

Gruppering:

α + (β₁ +  p₂) + (5₁ + Δ₂) + y = 2* 180º

Gruppering och förnyelse, det visas äntligen att:

α + β + Δ + y = 360º

Exempel 2

Demonstrera att medianen för en trapezoid är parallell med dess baser och dess längd är halvsemmen hos baserna.

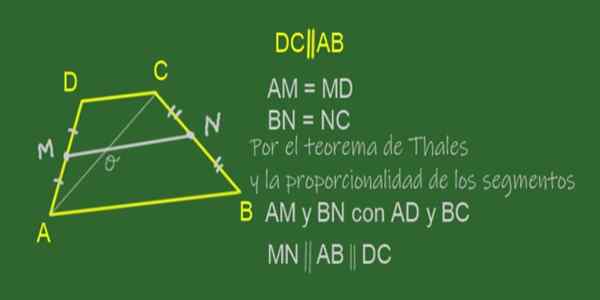Figur 11. Median MN av ABCD -trapes. Källa: f. Zapata.

Medianen för en trapes är det segment som går med i sidorna på sidorna, det vill säga de icke -parallella sidorna. I ABCD -trapesen som visas i figur 11 är medianen MN. 

Eftersom det är en mittpunkt på AD och N Mid BC Point, uppfylls det att kvoter AM / AD och BN / BC är lika.

Det vill säga, AM är proportionell mot BN i samma andel som AD är BC, så villkoren för tillämpningen av teorem (ömsesidigt) av Thales som bekräftar följande:

"Om i tre eller flera raka klipp av två sekant".

I vårt fall dras slutsatsen att MN-, AB- och DC -linjerna är parallella med varandra därför:

“LI en median är en av en trapes parallell med dess baser".

Kan tjäna dig: kombinerade operationer

Nu kommer Thales teorem att tillämpas:

"En uppsättning paralleller klippta av två eller flera torkningar bestämmer proportionella segment".

I vårt fall AD = 02:00, AC = 2 AO, så DAC -triangeln liknar Mao -triangeln och följaktligen DC = 2 mo.

Ett liknande argument gör det möjligt att bekräfta att Cu liknar CON, där CA = 2 CO och CB = 2 CN. Det följer att ab = 2 på.

Kort sagt, ab = 2 på y 2 mo. Så när vi har lämnat:

Ab + dc = 2 på + 2 mo = 2 (mo + on) = 2 mn

Slutligen rensar MN:

Mn = (ab + dc) /2

Och det dras slutsatsen att medianen i en trapezoid mäter basens halvkroppar, eller med andra ord: medianen mäter summan av baserna, dividerat med två.

Exempel 3

Visa att i en romb skärs diagonalerna i rät vinkel.

Figur 12. Romb och demonstration att deras diagonaler skärs i rät vinkel. Källa: f. Zapata.

Styrelsen i figur 12 visar den nödvändiga konstruktionen. Först dras ABCD -parallellogrammet med AB = BC, det är en romb. AC- och DB -diagonalerna bestämmer åtta vinklar som visas i figuren.

Med hjälp av satsen (a.Yo.p.som säger att interna alternativa vinklar mellan paralleller skärning av en sekant bestämmer lika vinklar, vi kan fastställa följande:

a₁ = γ₁, α2 = y2, 5₁ = Ss₁ och Δ2 = β2. (*)

Å andra sidan, eftersom de angränsande sidorna av en romb är av samma längd, bestäms fyra likhetstrianglar:

DAB, BCD, CDA och ABC

Nu åberopas triangles teorem (isosceles) som säger att vinklarna intill basen är av lika mått, där det dras slutsatsen att:

Δ₁ = β2, Δ2 = ß₁, α2 = y₁ och a₁ = γ2 (**)

Om relationer (*) och (**) kombineras, nås nästa jämställdhet av vinklar:

a₁ = α2 = y₁ = γ₁ Å ena sidan och ß₁ = Β2 = Δ₁ = Δ2 för den andra. 

Att komma ihåg teoremet för de lika trianglar som bekräftar att två trianglar med en lika sida mellan två lika vinklar är desamma:

AOD = AOB och följaktligen också vinklarna ∡Aod = ∡AOB.

Sedan ∡aod + ∡AOB = 180º, men som båda vinklarna är av lika mått, 2 ∡AOD = 180º vilket innebär att ∡aod = 90º.

Det vill säga det är geometriskt demonstrerat att diagonalerna i en romb skärs i rät vinkel.

Övningar löst

- Övning 1

Visa att i en rektangel trapesoid är icke-EG-vinklar kompletterande.

Lösning

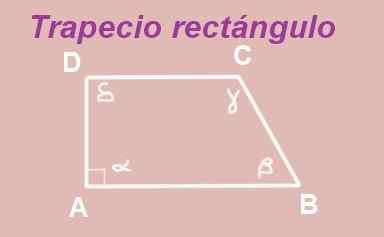Figur 13. Rektangel trapes. Källa: f. Zapata.

ABCD -trapezoid är byggd med parallella AB- och DC -baser. Den inre vinkeln på toppunkt A är rak (mäter 90º), så du har en rektangel trapezoid.

Vinklarna α och 5 är inre vinklar mellan två parallella AB- och DC -paralleller, därför är de desamma, det vill säga Δ = α = 90º. 

Å andra sidan har det visats att summan av de inre vinklarna i en fyrkantig lägger till 360º, det vill säga:

α + ß + y + Δ = 90º + ß + 90º + Δ = 360º.

Ovanstående leder till:

 β + Δ = 180º

Bekräfta vad som ville bli demonstrerat att vinklarna β och Δ är kompletterande.

- Övning 2

Ett ABCD -parallellogram har AB = 2 cm och AD = 1 cm, dessutom är vinkeln dålig 30º. Bestäm området för nämnda parallellogram och längden på dess två diagonaler.

Lösning

Området för ett parallellogram är produkten av längden på basen efter höjd. I detta fall kommer längden på segmentet B = AB = 2 cm att tas som bas, den andra sidan har längd a = AD = 1 cm och höjden h beräknas enligt följande:

H = ad * sin (30º) = 1 cm * (1/2) = ½ cm.

Sedan: area = b * h = 2 cm * ½ cm = 1 cm².

Referenser

1. C. OCH. TILL. (2003). Geometrielement: med övningar och kompassgeometri. University of Medellin.
2. Campos, f., Cerecedo, f. J. (2014). Matematik 2. Patria Redaktionsgrupp.
3. Freed, K. (2007). Upptäck polygoner. Utbildningsföretag.
4. Hendrik, V. (2013). Generaliserade polygoner. Birkhäuser.
5. Iriger. (s.F.). Matematik första termin Tacaná. Iriger.
6. Jr. Geometri. (2014). Polygoner. Lulu Press, Inc.
7. Miller, Heeren och Hornsby. (2006). Matematik: Resonemang och applikationer (tionde upplagan). Pearson Education.
8. Patiño, m. (2006). Matematik 5. Redaktionell progreso.
9. Wikipedia. Fyrkant. Återhämtad från: är.Wikipedia.com