Rep (geometri) längd, sats och övningar

En rep, I platt geometri är det linjesegmentet som går med två punkter från en kurva. Det sägs att linjen som innehåller detta segment är en torklinje till kurvan. Det är ofta en omkrets, men du kan säkert dra strängar i många andra kurvor, till exempel ellipser och liknelser.

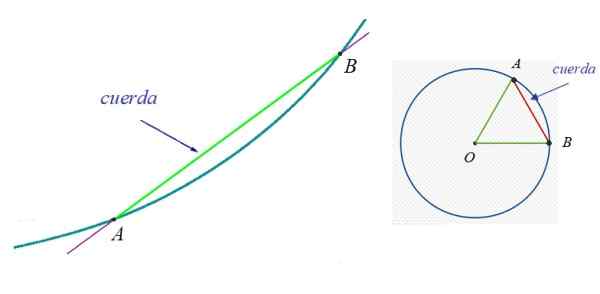
I figur 1 till vänster finns en kurva, till vilken punkterna A och B hör hemma. Repet mellan A och B är det gröna segmentet. Till höger är en omkrets och en av deras strängar, eftersom det är möjligt att spåra oändligt.

Figur 1. Till vänster repet på en godtycklig kurva och till höger repet. Källa: Wikimedia Commons.

I omkretsen är dess diameter särskilt intressant, vilket också kallas Stora rep. Det är ett rep som alltid innehåller centrum för omkretsen och mäter dubbelt radie.

Följande figur representeras av radien, diameter, ett rep och även en cirkelbåge. Att korrekt identifiera var och en är viktig när man löser problem.

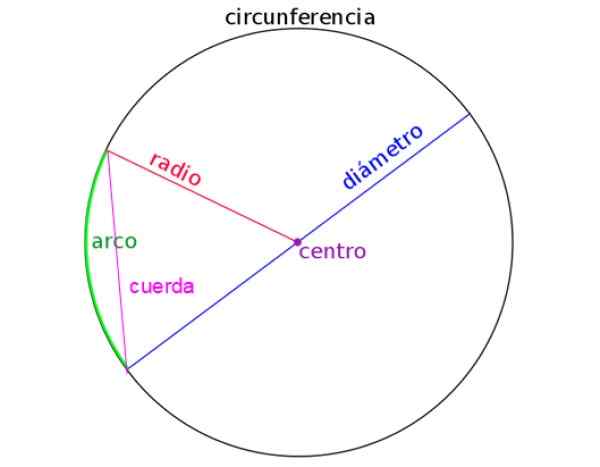figur 2. Element i omkretsen. Källa: Wikimedia Commons.

[TOC]

Replängd av en omkrets

Vi kan beräkna repets längd i en cirkel som börjar från figurerna 3A och 3B. Observera att en triangel alltid bildas med två lika sidor (liksiktiga): OA- och OB -segmenten, som mäter R, omkretsens radie. Den tredje sidan av triangeln är segment AB, kallad C, vilket är precis längden på repet.

Det är nödvändigt att rita en linje vinkelrätt mot C -repet för att halvera i vinkeln θ som finns mellan de två radioapparaterna och vars toppunkt är centrum eller omkrets. Det här är en centralvinkel -Eftersom dess toppunkt är centrum- och bisektorlinjen är också en sekant för omkretsen.

Det kan tjäna dig: radikala egenskaper

Omedelbart bildas två rektanglar, vars hypotenus. Eftersom bisektorn och med den diametern delar upp i två delar lika med repet visar det sig att ett av benen är hälften av C, såsom anges i figur 3B.

Från definitionen av bröstet i en vinkel:

synd (θ/2) = motsatt/hypotenusa cateto = (c/2)/r

Därför:

sin (θ/2) = c/2r

C = 2r sen (θ/2)

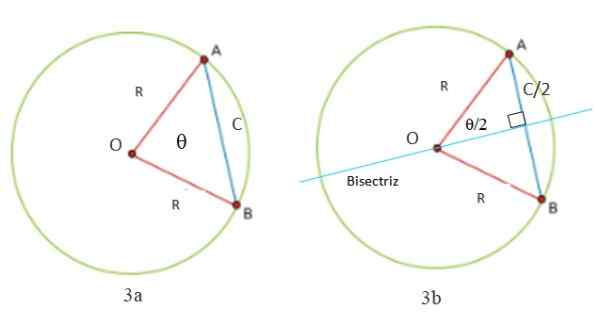Figur 3. Triangeln som bildas av två radioapparater och ett omkretsrep är isosceles (figur 3), eftersom den har två sidor lika. Bisektorn delar upp den i två rektanglar trianglar (figur 3b). Källa: Utarbetad av F. Zapata.

Strängteorem 

Strängsteoremet säger:

Om några två rep korsar sig vid en punkt, är produkten av längden på segmenten som visas på en av strängarna lika med produkten av längden på de segment som definieras i det andra repet.

Följande figur visar två strängar av samma omkrets: AB och CD, som korsar sig vid punkt P. I AB -repet definieras AP- och PB -segmenten, medan CP och PD definieras i CD -repet. Sedan, enligt satsen:

Ap . Pb = cp . P.s

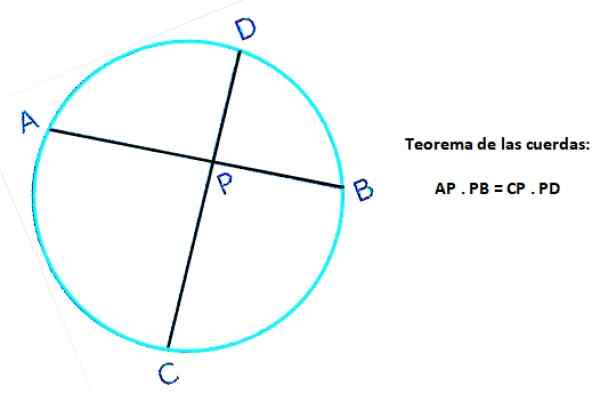Figur 4. Ropeoremet för en omkrets. Källa: f. Zapata.

Löst strängar övningar

- Övning 1

En cirkel har ett 48 cm rep, som är 7 cm från mitten. Beräkna cirkelområdet och omkretsens omkrets.

Lösning  

För att beräkna cirkeln ett område räcker det att känna till omkretsens radie till torget, eftersom det är uppfyllt:

A = π.R²

Nu är siffran som bildas med de data som tillhandahålls en rektangel triangel, vars ben är 7 respektive 24 cm.

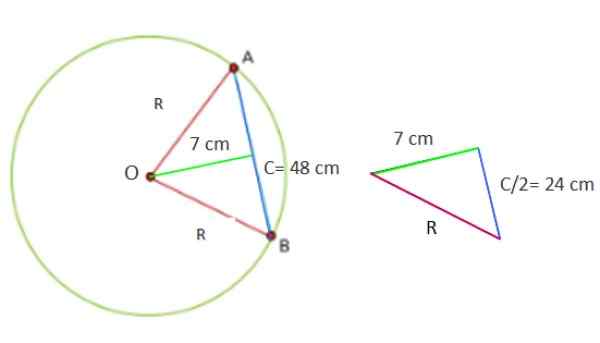Figur 5. Geometri för den lösta övningen 1. Källa: f. Zapata.

Därför att hitta värdet på R² Pythagoras C -satsen tillämpas direkt² = a² + b², Eftersom R är hypotenusen av triangeln:

Kan tjäna dig: nollvinkel: definition och egenskaper, exempel, övningar

R² = (7 cm)² + (24 cm)² = 625 cm²

Då är det begärda området:

A = π. 625 cm² = 1963.5 cm²

När det gäller omkretsen eller längden l för omkretsen beräknas den av:

L = 2π. R

Ersätta värden:

R = √625 cm² = 25 cm

L = 2π. 25 cm = 157.1 cm.

- Övning 2

Bestäm längden på repet för en cirkel vars ekvation är:

x² + och² - 6x - 14y -111 = 0

Det är känt att koordinaterna för repets mittpunkt är P (17/2; 7/2).

Lösning

Mittpunkten för prepet tillhör inte omkretsen, men repets extrema punkter. Problemet kan lösas med hjälp av Strings Theorem som tidigare anges, men först är det bekvämt.

Steg 1: Få den kanoniska ekvationen för omkretsen

Den kanoniska ekvationen av omkretsen med centrum (H, K) är:

(X-h)² + (Y-K)² = R²

För att få det är det nödvändigt att slutföra rutor:

(x² - 6x) + (och² - 14y) -111 = 0

Observera att 6x = 2.(3x) och 14y = 2.(7y), så att det föregående uttrycket skrivs om således och är oförändrad:

(x² - 6x+3²-3²) + (och² - 14y+7²-7²) -111 = 0

Och nu, minns definitionen av anmärkningsvärd produkt (A-B)² = a² - 2AB + B² Det kan skrivas:

(X - 3)² - 3² + (och - 7)² - 7² - 111 = 0

= (x - 3)² + (och - 7)² = 111 + 3² + 7² → (x - 3)² + (och - 7)² = 169

Omkretsen har ett centrum (3,7) och radio r = √169 = 13. Följande figur visar grafen över omkretsen och strängarna som kommer att användas i teoremet:

Kan tjäna dig: Vilka är de sju elementen i omkretsen?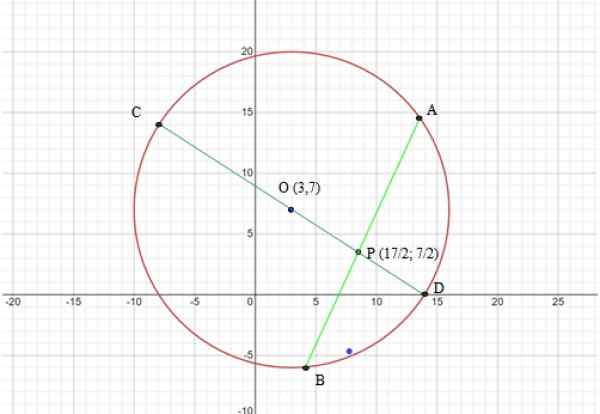Figur 6. Grafen över omkretsen av övningen löstes 2. Källa: f. Zapata genom den grafiska kalkylatorn online.

Steg 2: Bestäm de segment som ska användas i strängteoremet

Segmenten som ska användas är CD- och AB -strängarna, enligt figur 6 är båda klippta vid punkt P, därför:

Cp . Pd = ap. Pb

Nu kommer vi att hitta avståndet mellan punkter O och P, eftersom detta ger oss längden på OP -segmentet. Om vi ​​lägger till radien till denna längd kommer vi att ha CP -segmentet.

Avståndet D_Op Mellan två koordinatpunkter (x₁,och₁) och (x₂,och₂) är:

d_Op² = OP² = (x₂ - x₁)² + (och₂ - och₁)² = (3- 17/2)² + (7-7/2)² = 121/4 + 49/4 = 170/4

d_Op = Op = √170 /2

Med alla erhållna resultat, plus grafen, bygger vi följande lista över segment (se figur 6):

Co = 13 cm = r

Op = √170 /2 cm

CP = OP + R = 13 + √170 /2 cm

PD = OD - OP = 13 - √170 /2 cm

AP = PB

2.AP = replängd

Ersätter i strängsteoremet:

Cp . Pd = ap . PB = [(13 +√170 /2) . (13 -√170 /2)] = AP²

[169-170/4] = AP²

253/2 = AP²

AP = √ (253/2)

Repets längd är 2.AP = 2 (√253/2) = √506

Kan läsaren lösa problemet på ett annat sätt?

Referenser

1. Baldor, a. 2004. Flat och rymdgeometri med trigonometri. Kulturella publikationer s.TILL. av C.V. Mexiko.
2. C-k12. En ackord. Återhämtat sig från: CK12.org.
3. Escobar, J. Omkretsen. Återhämtat sig från: matematik.du.Edu.co.
4. Villena, m. Konisk. Hämtad från: Dspace.Espol.Edu.Ec.
5. Wikipedia. Rep (geometri). Återhämtad från: är.Wikipedia.org.