Nollvinkeldefinition och egenskaper, exempel, övningar

han nollvinkel Det är den vars åtgärd är värd 0, både i grader och i radianer eller andra vinklar mätsystem. Därför saknar det amplitud eller öppning, till exempel den mellan två parallella linjer.

Även om dess definition låter ganska enkel, är nollvinkeln mycket användbar i många fysik och tekniska tillämpningar, liksom i navigering och design.

Figur 1. Mellan hastigheten och accelerationen av bilen finns en nollvinkel, därför går bilen snabbare och snabbare. Källa: Wikimedia Commons.

Det finns fysiska mängder som måste anpassas parallellt för att uppnå vissa effekter: om en bil rör sig rakt på en motorväg och mellan dess hastighetsvektor v och dess vektoracceleration till Det finns 0º, bilen ökar.

I följande figur visas olika typer av vinkel inklusive nollvinkeln till höger. Som man kan se, saknar vinkel 0 amplitud eller öppning.

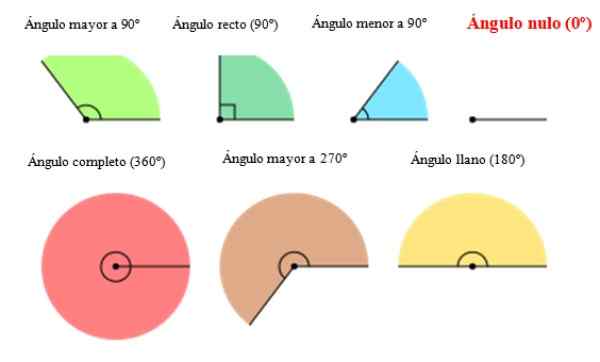figur 2. Typer av vinkel, inklusive nollvinkeln. Källa: Wikimedia Commons. Orias [CC BY-SA (https: // CreativeCommons.Org/licenser/BY-SA/3.0)].[TOC]

Exempel på nollvinklar

Det är känt att parallella linjer bildar en vinkel noll. När du har en horisontell linje är detta parallellt med x -axen i det kartesiska koordinatsystemet, därför är dess lutning med avseende på det 0. Med andra ord, horisontella linjer har en noll lutning.

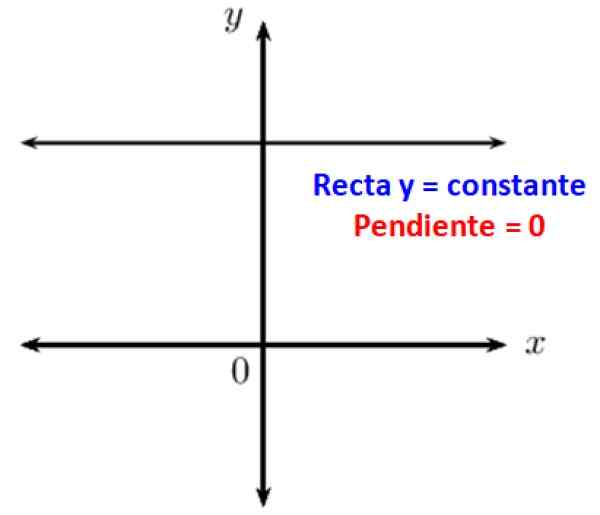Figur 3. Horisontella linjer har noll pågående. Källa: f. Zapata.

Även de trigonometriska orsakerna till nollvinkeln är 0, 1 eller oändlighet. Därför finns nollvinkeln i många fysiska situationer som involverar operationer med vektorer. Dessa skäl är:

Kan tjäna dig: ordnat par

-Sen 0º = 0

-cos 0º = 1

-TG 0º = 0

-Sec 0º = 1

-Skada 0º → ∞

-CTG 0º → ∞

Och de kommer att vara användbara för att analysera några exempel på situationer där närvaron av nollvinkeln spelar en grundläggande roll:

- Effekter av nollvinkel på fysiska storlekar

Summan av vektorer

När två vektorer är parallella är vinkeln mellan dem noll, som ses i figur 4 över ovan. I det här fallet utförs summan av båda genom att placera en efter den andra och storleken på vektorsummen är summan av storleken på tillägget (figur 4B).

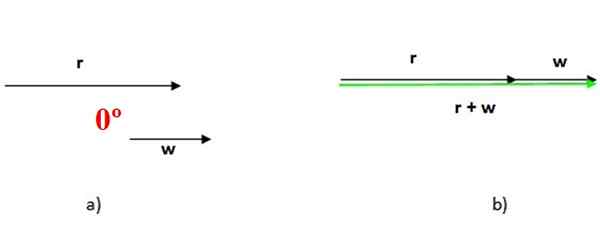Figur 4. Summan av parallella vektorer, i detta fall är vinkeln mellan dem en nollvinkel. Källa: f. Zapata.

När två vektorer är parallella är vinkeln mellan dem noll, som ses i figur 4 över ovan. I det här fallet utförs summan av båda genom att placera en efter den andra och storleken på vektorsummen är summan av storleken på tillägget (figur 4B)

Vridmomentet eller vridmomentet

Vridmomentet eller vridmomentet orsakar rotation av en kropp. Det beror på storleken på den applicerade kraften och hur den gäller. Ett mycket representativt exempel är figurens engelska nyckel.

För att uppnå den bästa svängeffekten, gäller kraft vinkelrätt på nyckelhandtaget, antingen upp eller ner, men rotation förväntas inte om kraften är parallell med handtaget.

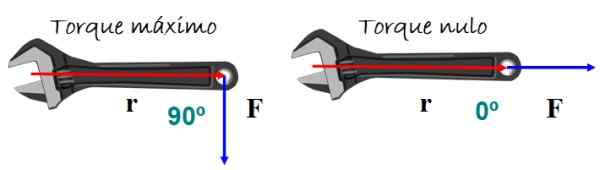Figur 5. När vinkeln mellan position och styrka vektorer är ogiltiga, förekommer inte vridmomentet och därför finns det ingen svängeffekt. Källa: f. Zapata.

Matematiskt vridmomentet τ Det definieras som vektor eller tvärprodukt mellan vektorerna r (positionsvektor) och F (Kraftvektor) i figur 5:

Kan tjäna dig: statistikgrenar

τ = r x F

Vridmomentets storlek är:

τ = r f sen θ

Att vara θ vinkeln mellan r och F. När synd θ = 0 är vridmomentet ogiltigt, i så fall θ = 0º (eller även 180º).

Elektriskt fältflöde

Det elektriska fältflödet är en skalarstorlek som beror på intensiteten hos det elektriska fältet såväl som ytorienteringen genom vilken den korsar.

I figur 6 finns det en cirkulär yta på området A genom vilken de elektriska fältlinjerna passerar OCH. Ytorienteringen ges av den normala vektorn n. Till vänster fältet och den normala vektorn bildar en acters godtycklig vinkel θ, i mitten bildar de en nollvinkel och höger är vinkelrätt.

När OCH och n De är vinkelräta, fältlinjerna korsar inte ytan och därför är flödet noll, medan när vinkeln mellan OCH och n Det är tomrum, linjerna korsar ytan helt.

Betecknar det elektriska fältflödet med den grekiska bokstaven φ (läser "FI"), dess definition för ett enhetligt fält som i figuren, det förblir så här:

Φ = OCH•nTILL

Punkten i mitten av båda vektorerna betecknar punkten eller skalprodukten, som växelvis definierar:

Φ = OCH•nA = eacosθ

Djärva och pilar ovanför bokstaven är resurser för att skilja mellan en vektor och dess storlek, som betecknas med normala bokstäver. Sedan cos 0 = 1 är flödet maximalt när OCH och n De är parallella.

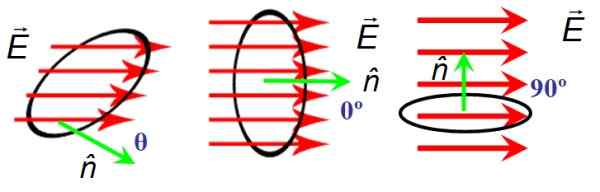Figur 6. Det elektriska fältflödet beror på orienteringen mellan ytan och det elektriska fältet. Källa: f. Zapata.

Övningar

- Övning 1

Två krafter P och Q De agerar samtidigt på ett snabbt objekt X, båda krafter utgör initialt en vinkel θ mellan dem. Vad händer med storleken på den resulterande kraften när θ minskar tills den avbryts?

Kan tjäna dig: Utvärdering av funktioner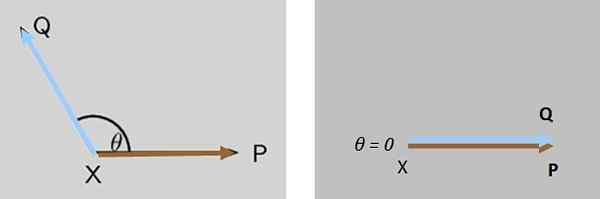 Figur 7. Vinkeln mellan två krafter som verkar på en kropp minskar tills storleken på den resulterande kraften får sitt maximala värde avbryts i detta fall. Källa: f. Zapata.

Lösning

Storleken på den resulterande kraften Q + P Det ökar gradvis tills det är maximalt när Q och P De är helt parallella (figur 7 till höger).

- Övning 2

Ange om nollvinkeln är en lösning av följande trigonometriska ekvation:

cos 2x = 1 + 4se x

Lösning

En trigonometrisk ekvation är en där det okända är en del av argumentet av en trigonometrisk anledning. För att lösa den föreslagna ekvationen är det bekvämt att använda formeln för dubbelvinkelkosinus:

cos 2x = cos² X - Sen² x

För på detta sätt blir argumentet på vänster sida x istället för 2x. Så:

cos² X - Sen² x = 1 + 4sen x

Å andra sidan cos² X + sen² x = 1, så:

cos² X - Sen² x = cos² X + sen² x + 4sen x

Termen cos² X avbryts och återstår:

- Sen² x = sen² x + 4sen x → - 2sen² x - 4senx = 0 → 2sen² x + 4senx = 0

Nu görs nästa ändring av variabel: SENX = U och ekvationen omvandlas till:

2U² + 4U = 0

2U (u+4) = 0

Vars lösningar är: u = 0 och u = -4. Återlämnande av förändringen skulle vi ha två möjligheter: sin x = 0 och Senx = -4. Denna sista lösning är inte livskraftig, eftersom bröstet i någon vinkel är mellan -1 och 1, så vi sitter kvar med det första alternativet:

synd x = 0

Därför är x = 0º en lösning, men tjänar också alla vinklar vars sinus är 0, som också kan vara 180º (π radianes), 360º (2 π radianer) och respektive negativ också.

Den mest allmänna lösningen av den trigonometriska ekvationen är: x = kπ där k = 0, ± 1, ± 2, ± 3, .. . k ett heltal.

Referenser

1. Baldor, a. 2004. Flat och rymdgeometri med trigonometri. Kulturella publikationer s.TILL. av C.V. Mexiko.
2. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Volym 3. Partikelsystem. Redigerad av Douglas Figueroa (USB).
3. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Volym 5. Elektrisk interaktion. Redigerad av Douglas Figueroa (USB).
4. Onlinemathlearning. Typer av vinklar. Hämtad från: onlinemathlearning.com.
5. Zill, D. 2012. Algebra, trigonometri och analytisk geometri. McGraw Hill Inter -American.