Norton Theorem Beskrivning, applikationer, exempel och övningar

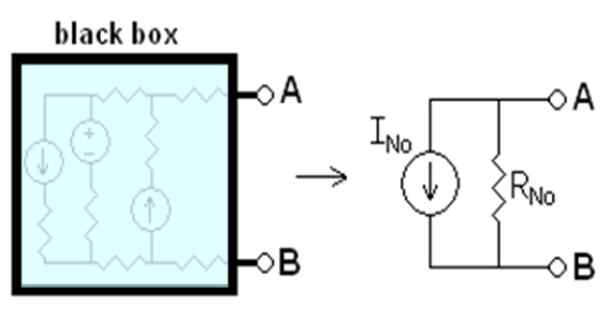
han Norton Theorem, som gäller elektriska kretsar, konstaterar att en linjär krets med två terminaler A och B kan ersättas av en annan helt motsvarande, bestående av en aktuell källa som heter I_Nej ansluten parallellt med ett motstånd R_Nej.

Sa nuvarande i_Nej Jag hörde_N Det är den som skulle flyta mellan punkterna A och B, om de var korta cirkulerade. Motståndet r_N Det är motsvarande motstånd mellan terminalerna, när alla oberoende källor är inaktiverade. Allt som sägs är schematiserat i figur 1.

Figur 1. Nortons motsvarande krets. Källa: Wikimedia Commons. Drumkid [CC BY-SA 3.0 (http: // Creativecommons.Org/licenser/BY-SA/3.0/]]

Den svarta rutan i figuren innehåller den linjära kretsen som kommer att ersättas av dess Norton -motsvarighet. En linjär krets är en där ingången och utgången har ett linjärt beroende, såsom förhållandet mellan spänning V och den likströmmen i i ett ohmiskt element: v = i.R.

Detta uttryck motsvarar Ohms lag, där R är motstånd, som också kan vara en impedans, om det är en växlande nuvarande krets.

Nortons sats utvecklades av elektriker och uppfinnare Edward L Engineer. Norton (1898-1983), som arbetade länge för Bell Laboratories.

[TOC]

Norton Theorem -applikationer

När de har mycket komplicerade nätverk, med många motstånd eller impedanser och du vill ha en mindre och mer hanterbar krets.

På detta sätt är Nortons sats mycket viktigt när man utformar kretsar med flera element, liksom att studera deras svar.

Förhållandet mellan Norton och Thevenins teorems

Nortons sats är det dubbla Thevenins teorem, vilket innebär att de är likvärdiga. Thevenins teorem indikerar att den svarta rutan i figur 1 kan ersättas av en seriepresskälla med ett motstånd, kallad Thevenin R -motstånd_Th. Detta uttrycks i följande figur:

Kan tjäna dig: Materialmekanik: historia, studieområde, applikationer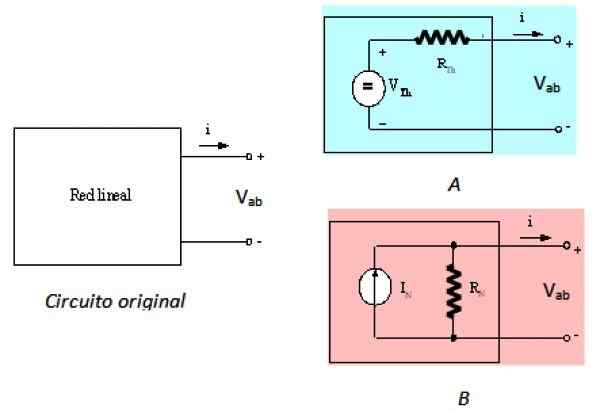 figur 2. Original vänsterkretsen och dess ekvivalenter från Thévenin och Norton. Källa: f. Zapata.

Den vänstra kretsen är den ursprungliga kretsen, det linjära nätverket i den svarta lådan, kretsen upp till höger är motsvarande thevenin och kretsen B Det är Nortons motsvarande, som beskrivs. Sett från terminaler A och B är de tre kretsarna likvärdiga.

Observera nu det:

-I den ursprungliga kretsen är spänningen mellan terminalerna v_Ab.

-V_Ab  = V_Th i kretsen TILL

-Slutligen, v_Ab  = Jag_N.R_N i kretsen B

Om terminaler A och B är kortslutning i de tre kretsarna, måste det uppfyllas att spänningen och strömmen mellan dessa punkter måste vara densamma för de tre, eftersom de är likvärdiga. Så:

-I den ursprungliga kretsen är strömmen i.

-För krets A är strömmen i = v_Th / R_Th, Enligt Ohms lag.

-Slutligen i krets B är strömmen i_N

Därför dras slutsatsen att motståndet från Norton och Thevenin har samma värde, och att strömmen ges av:

i = i_N = V_Th / R_Th = V_Th / R_N

Exempel

För att korrekt tillämpa Nortons sats följs följande steg:

-Kretsavsnittet för vilket Norton -motsvarigheten hittas från nätverket är isolat från nätverket.

-Ange terminaler A och B i den återstående kretsen.

-Byt ut spänningskällorna med kortkretsar och nuvarande med öppna kretsar, för att hitta motsvarande motstånd mellan terminaler A och B. Detta är r_N.

-Returnera alla källor till sina ursprungliga positioner, kortscircuit terminalerna A och B och hitta strömmen som cirkulerar mellan dem. Detta är jag_N.

Kan tjäna dig: Doppler -effekt: Beskrivning, formler, fall, exempel

-Rita Norton -motsvarande krets enligt vad som anges i figur 1. Båda, nuvarande källa och motsvarande motstånd är parallellt.

Du kan också tillämpa TheVevenins sats för att hitta r_Th, som vi redan vet är lika med R_N, Sedan enligt ohms lag kan du hitta jag_N Och den resulterande kretsen dras.

Och nu låt oss titta på ett exempel:

Hitta Nortons motsvarighet mellan punkterna A och B i följande krets:

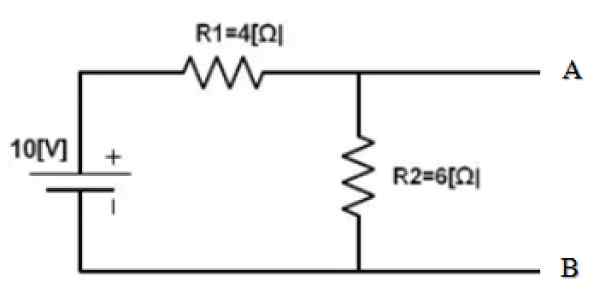Figur 3. Exempelkrets. Källa: f. Zapata.

Kretsens del är redan isolerad vars motsvarande måste hittas. Och punkterna A och B är tydligt bestämda. Det följande är att kortsluta 10 V -källan och hitta motsvarande motstånd för den erhållna kretsen:

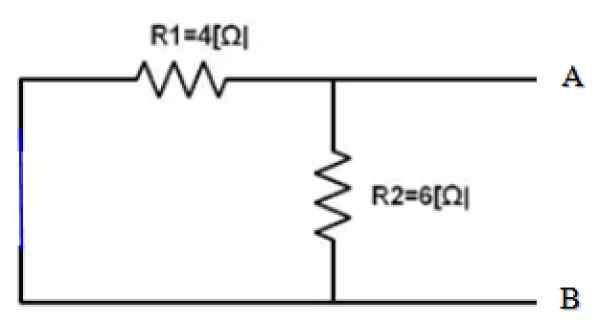Figur 4. Kretskälla. Källa: f. Zapata.

Vyer från terminaler A och B, båda motstånd R₁ och r₂ De är därför parallellt:

1/r_eq = 1/r₁₂ = (1/4) + (1/6) Ω^-1 = 5/12 Ω^-1  → R_eq = 12/5 Ω = 2.4 Ω

Sedan returneras källan till sin plats och punkterna A och B är korta kretsar för att hitta strömmen som cirkulerar där, detta kommer att vara_N. Isåfall:

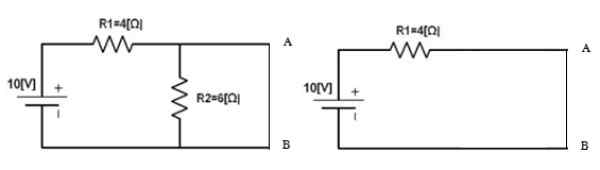Figur 5. Krets för att beräkna Norton -strömmen. Källa: f. Zapata.

Yo_N = 10 V / 4 Ω = 2.5 a

Norton Equivalent

Slutligen dras Nortons motsvarande med de hittade värdena:

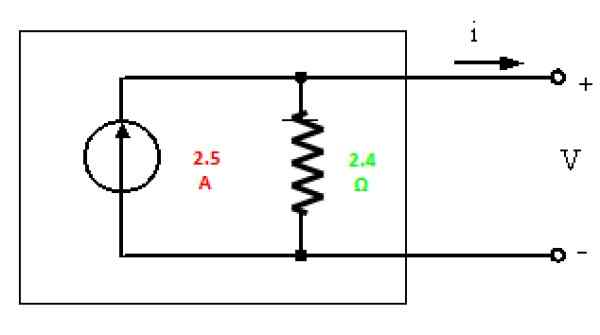Figur 6. Norton Equivalent of the Circuit i figur 3. Källa: f. Zapata.

Träning löst

I kretsen i följande figur:

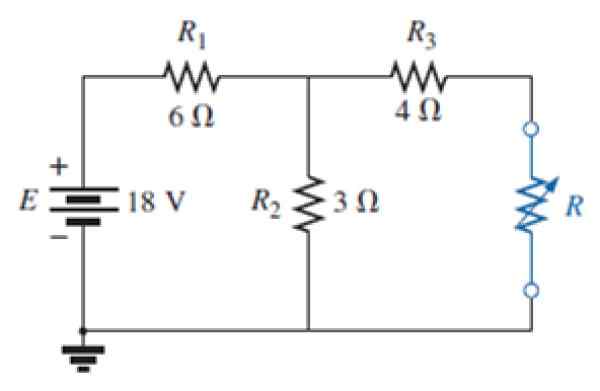Figur 7. Kretsen för övningen löst. Källa: Alexander, C. 2006. Elektriska kretsfundament. 3: e. Utgåva. MC Graw Hill.

a) Hitta Nortons motsvarande krets av det yttre blå motståndsnätverket.

b) Hitta också Thévenins motsvarande.

Lösning till

Efter de steg som anges ovan måste källan vara kort krets:

Kan tjäna dig: diffraktion av ljud: vad som består av exempel, applikationer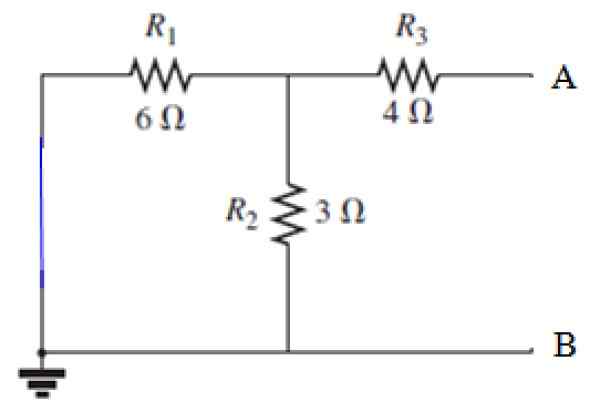 Figur 8. Kort -kretskälla i kretsen i figur 7. Källa: f. Zapata.

RN -beräkning

Utsikt från terminalerna A och B, motstånd R₃ är i serie med den parallella bildade av motståndet r₁ och r₂, Låt oss först beräkna motsvarande motstånd för denna parallell:

1/r₁₂ = (1/6)+ (1/3) Ω^-1 = 1/2 Ω^-1  → R_eq = 2/1 Ω = 2Ω

Och sedan är denna parallell i serie med R_3, så att motsvarande motstånd är:

R_eq = 2 Ω + 4 Ω = 6 Ω

Detta är värdet på båda r_N från och med R_Th, som förklarats tidigare.

Beräkning av in

Sedan är terminaler A och B korta kretsar och returnerar källan till sin plats:

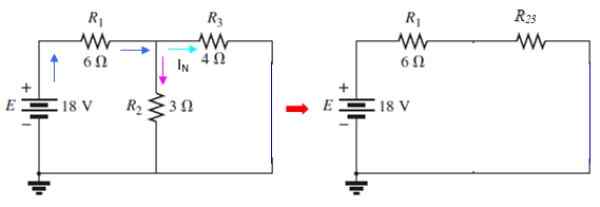Figur 9. Norton nuvarande kretsar. Källa: f. Zapata.

Den nuvarande passering genom i₃ är den nuvarande i_N eftertraktad, som kan bestämmas med nätmetoden eller använda serier och parallella. I denna krets r₂ och r₃ De är parallellt:

1/r₂₃ = (1/3)+ (1/4) Ω^-1 = 7/12 Ω^-1  → R₂₃ = 12/7 Ω

Motståndet r₁ Det är i serie med denna parallell, då:

R₁₂₃ = 6 + (12/7) Ω = 54/7 Ω

Strömmen som kommer ut ur källan (blå färg) beräknas av Ohms lag:

V = i. R → I = V/R = 18 V/(54/7 Ω) = 7/3 a

Denna ström är uppdelad i två delar: en som korsar r₂ Och en annan som korsar r₃. Men strömmen som korsar parallellen r₂₃ Det är detsamma som går igenom r₁, Som framgår av figurens mellankrets. Spänningen finns:

V₂₃ = Jag.R₂₃ = (7/3) a .(12/7) Ω = 4 V

Båda motståndet r₂ och r₃ De är vid den spänningen, eftersom de är parallellt, därför:

Yo₃ = V₂₃ / R₃ = 4 V / 4 Ω = 1 A

Vi har redan sökt Norton -strömmen, eftersom som tidigare sagt jag₃ = Jag_N, så:

Yo_N = 1 a

Norton Equivalent

Allt är redo att dra Norton -motsvarigheten till denna krets mellan punkterna A och B:

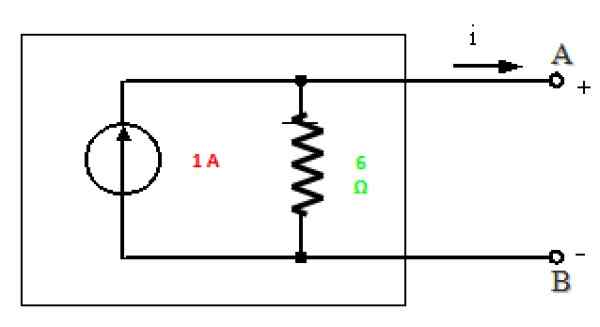Figur 10. Norton Equivalent of the Circuit i figur 7. Källa: f. Zapata.

Lösning B

Att hitta Thévenins motsvarande är mycket enkelt, eftersom R_Th = R_N= 6 Ω och som förklaras i föregående avsnitt:

V_Th = Jag_N. R_N = 1 a . 6 Ω = 6 V

Thévenins motsvarande krets är:

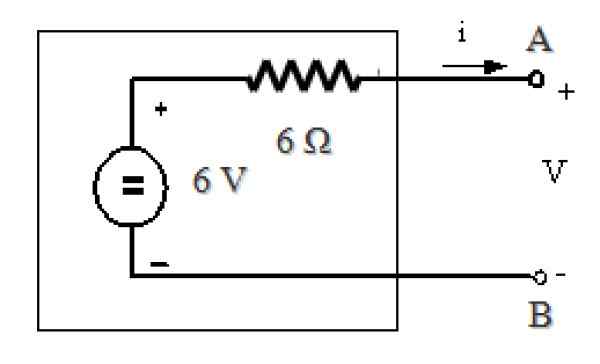Figur 11. Thevenins motsvarighet av kretsen i figur 7. Källa: f. Zapata.

Referenser

1. Alexander, c. 2006. Elektriska kretsfundament. 3: e. Utgåva. MC Graw Hill.
2. Boylestad, r. 2011. Introduktion till kretsanalys. 2: a. Utgåva. Pearson.
3. Dorf, r. 2006. Introduktion till elektriska cirkuds. 7th. Utgåva. John Wiley & Sons.
4. Edminister, J. nitton nittiosex. Elektriska kretsar. Schaumserie. 3: e. Utgåva. MC Graw Hill.
5. Wikipedia. Norton Theorem . Återhämtat sig från: det är.Wikipedia.org.