Härrörande från cotangent beräkning, demonstration, övningar

De Cotangent härledd Det är lika med det motsatta av kvadratet på skörden “-CSC²". Denna formel beror på derivatlagar per definition och differentiering av trigonometriska funktioner. Det betecknas enligt följande:

D (ctg u) = -csc² eller . du

Där "du" symboliserar uttrycket härrörande från argumentfunktionen, med avseende på den oberoende variabeln.

Källa: Pixabay.com

[TOC]

Hur beräknas det?

Förfarandet för att utveckla dessa derivat är ganska enkelt. Bara identifiera argumentet och vilken typ av funktion som den representerar.

Exempelvis presenterar uttrycket CTG (f/g) en uppdelning i sitt argument. Detta kommer att behöva en differentiering angående U/V, efter att ha utvecklat zip.

Cotangent är tangentens ömsesidiga funktion. Algebraiskt betyder det att:

(1/tg x) = ctg x

Ctg x = cos x / sen x

Det är felaktigt att säga att cotangentfunktionen är "omvänd" av tangenten. Detta beror på att den omvända funktionen av tangenten per definition är tangentbågen.

(TG^-1 x) = arctg x

Enligt Pythagorean trigonometri är cotangenten involverad i följande avsnitt:

Ctg x = (cos x) / (sin x)

Ctg² X + 1 = CSC² x

Enligt analytisk trigonometri svarar på följande identiteter:

Ctg (a + b) = (1 - tg a . Tg b) / (tg a + tg b)

Ctg (a - b) = (1 + tg a . Tg b) / (tg a - tg b)

CTG (2A) = (1 - TG² a) / (2tg a)

Egenskaper för cotangentfunktionen

Det är nödvändigt att analysera olika egenskaper hos funktionen f (x) = ctg x för att kunna definiera de nödvändiga aspekterna för att studera dess differentiering och tillämpning.

Vertikala asymptoter

Cotangent -funktionen definieras inte i de värden som gör uttrycket "Senx" noll. På grund av dess motsvarande CTG x = (cos x) / (sin x) kommer den att ha en obestämdhet i alla "nπ" med n som tillhör heltal.

Det kan tjäna dig: analytisk geometri

Det vill säga i vart och ett av dessa värden på x = nπ kommer det att finnas en asymptot vertikal. När värdet på cotangenta närmar sig, och när du närmar sig höger kommer funktionen att öka på obestämd tid.

Domän

Domänen för cotangentfunktionen uttrycks av uppsättningen x ∈ R / x ≠ nπ, n ∈ Z. Detta läses som "X som tillhör uppsättningen av verkliga siffror så att X skiljer sig från Nπ, med N som tillhör hela siffrorna".

Räckvidd

Rang för cotangentfunktionen täcker från mindre till mer oändlighet. Det är därför det kan dras slutsatsen att dess rang är uppsättningen av verkliga n -nummer.

Frekvens

Cotangent -funktionen är periodisk och dess period är lika med π. På detta sätt uppfylls jämlikheten CTG x = ctg (x + nπ), där n tillhör z.

Beteende

Det är en udda funktion, eftersom ctg (-x) = - ctg x. På detta sätt är det känt att funktionen presenterar en symmetri med avseende på koordinatens ursprung. Det presenterar också en minskning av varje intervall som ligger mellan 2 på varandra följande vertikala asymptoter.

Det har inte maximala eller minimivärden, eftersom deras tillvägagångssätt till vertikala asymptoter har beteenden där funktionen växer eller minskar på obestämd tid.

Nollorna eller rötterna på cotangentfunktionen finns i de udda multiplarna av π/2. Detta innebär att CTG x = 0 uppfylls i värdena på formen x = nπ/2 med en helhet.

Demonstration

Det finns två sätt att demonstrera derivatet av cotangentfunktionen.

Trigonometrisk differentiell demonstration

Derivatet av cotangentfunktionen demonstreras från motsvarande i bröst och kosenos.

Kan tjäna dig: Boolean Algebra: Historia, teorem och postulat, exempel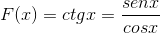

Det handlar om derivatet av en funktionsavdelning

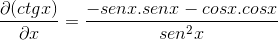
Efter att de faktorerna är grupperade och de pytagoreiska identiteterna söks efterlikna

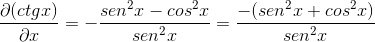
Ersätta identiteter och tillämpa ömsesidighet Uttrycket erhålls

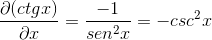
Definition av derivatdefinition

Följande uttryck motsvarar derivatet per definition. Där avståndet mellan 2 poäng i funktionen närmar sig noll.

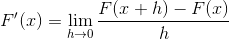
Byt ut för den cotangente du måste:

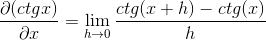
Identiteter gäller för summan av argument och ömsesidighet

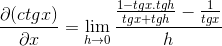
Fraktionen av telleren drivs traditionellt

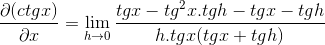
Eliminera motsatta element och ritning av gemensamma faktor erhålls

Tillämpa Pythagorean identiteter och ömsesidighet

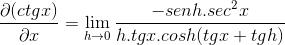
De element som utvärderas i x är konstant med avseende på gränsen, därför kan de lämna argumentet om detta. Då tillämpas trigonometriska gränser.

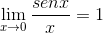
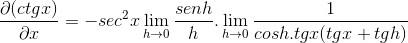
Gränsen utvärderas

Då är det factoring tills det når önskat värde

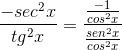
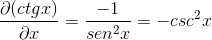
Detta demonstreras av cotangente -derivatet som motsatsen till skördesfyrkanten.

Löst övningar

Övning 1

Enligt funktionen f (x), definiera uttryck f '(x)

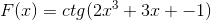
Motsvarande härledning tillämpas med respekt för kedjeregeln

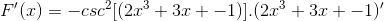
Härleda argumentet

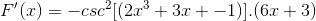
Ibland är det nödvändigt att tillämpa ömsesidiga eller trigonometriska identiteter för att anpassa lösningarna.

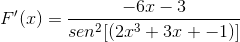
Övning 2

Definiera det differentiella uttrycket som motsvarar f (x)

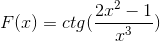
Enligt härledningsformeln och respektera kedjeregeln

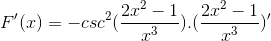
Argumentet härleds, medan resten förblir detsamma

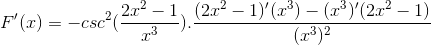
Härleda alla element

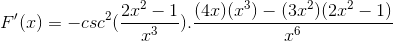
Arbetar på traditionellt sätt produkterna från samma bas

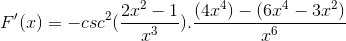
Samma element läggs till och den vanliga faktorn extraheras

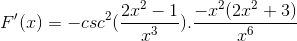
Tecken förenklas och drivs. Ger plats för det helt härledda uttrycket

Kan tjäna dig: Skillnad mellan en gemensam fraktion och ett decimalnummer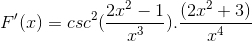

Referenser

1. Trigonometriska serier, volym 1. TILL. Zygmund. Cambridge University Press, 2002
2. Kalkyl av en enda variabel. Ron Larson, Bruce H. Edwards. Cengage Learning, 10 november. 2008
3. Kalkyl med trigonometri och analytisk geometri. John H. Saxon, John Saxon, Frank Wang, Diana Harvey. Saxonska förläggare, 1988
4. Multivariabel analys. Sable Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13 december. 2010
5. Systemdynamik: Modellering, simulering och kontroll av mekatroniska system. Dean C. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7 Mar. 2012
6. Calculus: Matematik och modellering. William Bauldry, Joseph R. Fiedler, Frank R. Giordano, Ed Lodi, Rick Vitray. Addison Wesley Longman, 1 jan. 1999