Implicita derivat hur de löses och löses övningar

De implicita derivat De är verktyg som används i en differentieringsteknik som används på funktioner. De gäller när det inte är möjligt, enligt regelbundna metoder, genomföra clearance av den beroende variabeln som ska härledas. Denna avstånd görs baserat på den oberoende variabeln.

Till exempel i uttrycket 3xy³ - 2y + xy² = xy, du kan inte få uttrycket som definierar "y" beroende på "x". Så att när differentiellt uttryck dy/dx kan erhållas.

[TOC]

Hur löses implicita derivat?

För att lösa en implikation är det baserat på ett implicit uttryck. Till exempel: 3xy³ - 2y + xy² - Xy = 0. Detta har redan tydligt rensats, men att göra det är inte ett nödvändigt villkor för att erhålla derivatet av y angående x. Sedan härleds vart och ett av elementen med respekt för kedjeregeln för blandade funktioner:

3xy³ Den består av 2 variabler, därför D (3xy³) Det kommer att behandlas som derivat av en produkt av funktioner.

D (3xy³)/dx = 3y³ + 3y².(3x) och '= 3y³ + 9xy² och'

Där elementet och "är känt som"och kusin”Och dy/dx representerar

-2y härstammar enligt lag K.U = k.ELLER'

D (-2y) = -2 och '

Xy² antar att en annan differential består av en produkt av funktioner

D (xy²) = y² + 2xy och '

-XY är ett homologt sätt

d (-xy) = -y -x och '

De ersätts i jämlikhet och vet att nollderivat är noll.

3y³ + 9xy² och ' - 2 och' + och² + 2xy och ' - y - x och' = 0

De element som har termen och 'grupperas tillsammans på ena sidan av jämlikhet

Kan tjäna dig: colineala vektorer

3y³ + och² - y = -9xy² och ' + 2 och' + x och '

Den vanliga faktorn och 'i rätt jämlikhetsmedlem extraheras

3y³ + och² - y = y '(-9xy² + x + 2)

Slutligen, termen som multipliceras och '. Därmed erhålla uttrycket som motsvarar det implicita derivatet av y angående x.

och '= dy/dx = (3y³ + och² - y)/(-9xy² + x + 2)

Kedjeregel

I det implicit härledningen respekteras alltid kedjregeln. Alla differentiella uttryck kommer att ges beroende på den oberoende variabeln x. Så att någon variabel θ skiljer sig från X måste inkludera termen dθ/dx efter att ha härledts.

Denna term kommer endast att visas i första graden eller med exponent lika med 1. Denna kvalitet gör det helt tydligt enligt traditionella faktoriseringsmetoder. Så att det blir möjligt att få uttrycket som definierar differentiell dθ/dx.

I kedjeregeln visas den progressiva karaktären av differentierings- eller derivatprocessen. Var för alla sammansatta funktioner f [g (x)] kommer det differentiella uttrycket för f

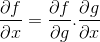
Driftsordning

I varje formel eller härledande lag som tillämpas måste variablens ordning beaktas. Kriterierna associerade med den oberoende variabeln respekteras utan att ändra dess korrelation med den beroende variabeln.

Förhållandet mellan den beroende variabeln vid härledd tid tas direkt.; Med undantag för att detta kommer att betraktas som en andra funktion, varför kedjeregelkriterierna för blandade funktioner tillämpas.

Detta kan utvecklas i uttryck med mer än 2 variabler. Under samma principer kommer alla skillnader som hänvisar till beroende variabler.

Kan tjäna dig: vad är riktlinjen? (Geometri)

Grafiskt hanteras samma kriterier som definierar derivatet. Medan derivatet är lutningen för linjen tangent till kurvan i planet, representerar resten av de skillnader som tillhör de beroende variablerna (dy/dx, dz/dx) tangentplan till de vektorkroppar som beskrivs av funktionerna i flera variabel.

Implicit av en funktion

Det sägs att en funktion implicit definieras, om uttrycket y = f (x) kan representeras som en multipel variabel funktion f (x, y) = 0 medan f definieras i plan r².

3xy³ - 2y + xy² = x och kan skrivas i 3xy -formuläret³ - 2y + xy² - Xy = 0

Med tanke på omöjligt att förklara funktionen y = f (x).

Historia

Differentialberäkningen började utses av olika matematiska forskare, runt sjuttonhundratalet. Första gången det nämndes var genom Newton och Leibniz bidrag. Båda behandlade differentiell beräkning från olika synpunkter, men konvergerade i deras resultat.

Medan Newton fokuserade på differentiering som en hastighet eller variation, var Leibniz -metoden mer geometrisk. Det kan sägas att Newton attackerade de antaganden som lämnats av Apollonius of Perge och Leibniz de geometriska idéerna från Fermat.

Det implicita härledningen visas omedelbart när de differentiella och omfattande ekvationerna överväger. De utökade det geometriska begreppet Leibniz till R³ och till och med flerdimensionella utrymmen.

Ansökningar

Implicita derivat används i olika situationer. De är vanliga i valutakursproblem mellan relaterade variabler, där variablerna beroende på studiens känsla kommer att betraktas som beroende eller oberoende.

De har också intressanta geometriska tillämpningar, till exempel i problem med reflektioner eller skuggor, på figurer vars form kan modelleras matematiskt.

Kan tjäna dig: kvotprovtagning: metod, fördelar, nackdelar, exempel

De är ofta användbara inom områdena ekonomi och teknik, liksom i olika undersökningar av naturfenomen och experimentella byggnader.

Löst övningar

Övning 1

Definiera det implicita uttrycket som definierar Dy/dx

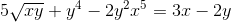
Varje element skiljer sig från uttrycket

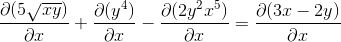
Upprätta kedjeregeln i varje kompetent fall

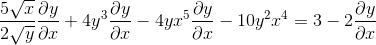
Gruppera på ena sidan av jämlikhet elementen som har dy/dx

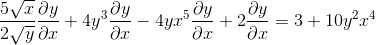
Är factoring med den vanliga faktorn

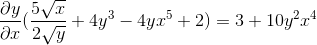
Rensas genom att få det sökande uttrycket

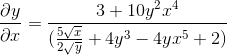
Övning 2

Definiera det implicita uttrycket som definierar Dy/dx

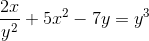
Uttrycker derivaten för att genomföra

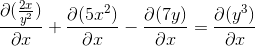
Implicit härleder enligt kedjeregeln

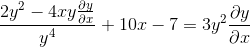
Factoring vanliga element

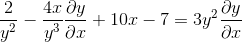
Gruppera termen dy/dx på ena sidan av jämlikhet

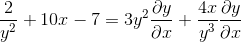
Vanlig faktor för differentiellt element

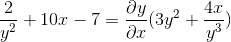
Vi rensar och får det sökande uttrycket

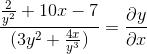
Referenser

1. Kalkyl av en enda variabel. Ron Larson, Bruce H. Edwards. Cengage Learning, 10 november. 2008
2. Implicit Function Theorem: Historia, Theory and Applications. Steven G. Krantz, Harold R. Parker. Springer Science & Business Media, 9 november. 2012
3. Multivariabel analys. Sable Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13 december. 2010
4. Systemdynamik: Modellering, simulering och kontroll av mekatroniska system. Dean C. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7 Mar. 2012
5. Calculus: Matematik och modellering. William Bauldry, Joseph R. Fiedler, Frank R.Giordano, Ed Lodi, Rick Vitray. Addison Wesley Longman, 1 jan. 1999