Vinkelförskjutning

Vad är vinkelförskjutning?

han Vinkelförskjutning Det är förändringen eller variationen i vinkelläget som ett objekt i rotationsupplevelser, vanligtvis mätt i radianer eller något annat mått som ges för varv, till exempel betyg eller revolutioner.

När ett föremål kretsar kring en fast axel bestäms dess vinkelförskjutning genom att mäta vinkeln som sveps av en linje som passerar genom vilken punkt som helst i kroppen som korsar rotationsaxeln, det vill säga en radiell linje.

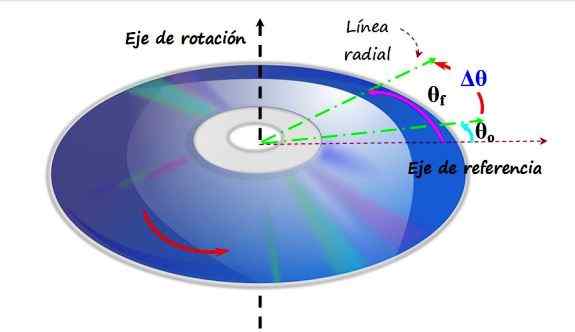En kompakt skiva eller CD kretsar i en antihoranant riktning runt en vertikal rotationsaxel. När du passerar från vinkel θo till θf sägs det att det har upplevt en vinkelförskjutning. Källa: f. Zapata.

I den övre figuren finns en CD som roterar i en anti -Horary -riktning, som är dess rotationsaxel den vertikala axeln. En referensaxel placeras på CD -planet, vilket motsvarar vinkeln 0 radianer eller 0. Den gröna linjen är en radiell linje, som ursprungligen bildar en vinkel θ_antingen Med referensen. Detta är din första position.

Senare flyttar den gröna linjen till en ny position som heter θ_F, Och upplevelsen som upplevs, kallad Δθ är helt enkelt:

Δθ = θ_F - θ_antingen

Varje punkt P av CD -skivan upplever samma vinkelförskjutning i ett visst tidsintervall, utom mitten, som är där rotationsaxeln passerar och förblir i vila.

Formler och ekvationer

Det finns ett objekt som kretsar kring en fast axel eller som lämnar skärmen till läsaren. Och inom det finns det punkt P, beläget på ett avstånd R av rotationsaxeln och beskriver radio R -omkretsar.

Detta ses i följande figur, som visar ett skärningsobjekt, sett i strid med klocknålarna. Den aktuella punkten är i vinkelläget θ, mätt från referensaxeln, som i detta fall är den horisontella axeln.

Kan tjäna dig: tillsatsprincip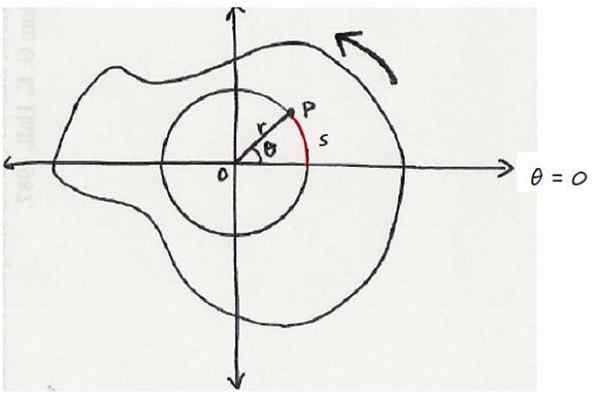Ett objekt som roterar i en anti -horary mening. Rotationsaxeln kommer vinkelrätt mot skärmen. Källa: Wikimedia Commons.

Genom konvention, till rotationen i en antihorarial mening tilldelas den positiv mening, medan rotationen i ett schema har ett negativt tecken.

När punkten P svär vinkeln θ, reser den samtidigt bågen. Eftersom θ är en central vinkel, eftersom dess toppunkt upptar mitten av omkretsen, uppfylls det att:

Med θ uttryckt i radianer.

Vinkelförskjutningen är:

Δθ = θ_slutlig  - θ_första

Till exempel om P började med θ_första = 0 rad och är sedan i θ_slutlig = 0.8 rad, dess vinkelförskjutning kommer från:

Δθ = 0.8 rad - 0 rad =  0.8 rad

Andra punkter i objektet kan ockupera olika vinkelpositioner, men alla upplever samma vinkelförskjutning. De mest avlägsna partiklarna från mitten reser emellertid större avstånd, eftersom s = r⋅θ.

Vinklar

I rotationen är det vanligt att hitta vinklarna uppmätta i radianer, men de finns också i grader och revolutioner eller svängar. Vid problemlösning är det nödvändigt att flytta från dessa enheter till radianer.

1 Revolution motsvarar en fullständig sväng, det vill säga när en fullständig sväng bryts har den blivit 360 º och dessa motsvarar 2π -radianer, eftersom i så fall turnerade punkten en båge lika med 2πr:

Men förenkla, den tidigare ekvivalensen kan uttryckas enligt följande:

π radianes = 180º

Hur beräknas vinkelförskjutning?

Vinkelförskjutningen kan beräknas analogt till hur förskjutningen i rörelsen beräknas i en dimension, efter en viss rörelsemodell. För detta definieras den genomsnittliga vinkelhastigheten som vinkelförskjutningen Δθ i ett givet tidsintervall ΔT:

Där genomsnittlig vinkelhastighet betecknas som ω_m och ges i radianer/s i enheter i det internationella systemet om.

Kan tjäna dig: Hur man får en triangelvinkel? (Exempel)

Omedelbar vinkelhastighet är gränsen för genomsnittlig vinkelhastighet när ΔT → 0:

Det vill säga det är det första härrörande från vinkelläget med avseende på tid. I sin tur kan en vinkelacceleration definieras, betecknas som a, vilket motsvarar derivatet eller förändringshastigheten för vinkelhastigheten med avseende på tid:

Som också kan tolkas som den andra härrörande från vinkelläget med avseende på tid.

Det viktiga är att två rörelsemodeller kan etableras i analogi med de rektilinära rörelserna, eftersom även om rotationerna utförs i planet, är en enda vinkelkoordinat tillräcklig för att fastställa objektets position.

Enhetlig cirkulär rörelse

I den enhetliga cirkulära rörelsen är vinkelhastigheten konstant, det vill säga den genomsnittliga vinkelhastigheten är lika med omedelbar vinkelhastighet. Eftersom vinkelacceleration α är lika med 0 kan du skriva följande ekvation för positionen som en funktion av tiden:

θ = θ_antingen + ωt

Där θ_antingen Det är den ursprungliga positionen för mobilen.

Enhetligt accelererad cirkulär rörelse

I detta fall är vinkelacceleration α konstant, och i analogi med den enhetligt varierade rätlinjiga rörelsen kan följande ekvationer skrivas:

• θ = θ_antingen + Ω_antingen T + ½ αT²
• Ω = ω_antingen + αT 
• Ω² = Ω_antingen² + 2α ∙ Δθ

Träning löst

Första träning

Det kan antas att jorden är ett styvt objekt som kretsar på en fast axel och att dess rotation är nästan enhetlig. I tidsintervallet ΔT = 12 timmar Hitta:

a) Jordens vinkelförskjutning

b) Din vinkelhastighet

c) Vinkelacceleration under det tidsintervallet.

Lösning till

Att veta att om 24 timmar tar jorden en fullständig sväng runt sin axel, på 12 timmar kommer du att ha vänt hälften av en varv, det vill säga π -radianer. Om det anses vara en del av θ_första = 0 rad, då är dess vinkelförskjutning:

Kan tjäna dig: multiplikativ princip: räkningstekniker och exempel

Δθ = π radianer

Lösning B

Eftersom rotation är enhetlig är vinkelhastigheten kvoten mellan vinkelförskjutning och tid, dessutom 1 timme = 3600 s:

Ω = π rad / 12 h = π rad / (12 x 3600) s = 0.000073 rad/s.

Lösning C

Vinkelacceleration är ogiltig, eftersom jordens rotation är enhetlig.

Andra träning

Juan har kört ett avstånd på 35 meter på ett cirkulärt friidrottsspår vars radie är lika med 7 meter. Beräkna den vinkelförskjutning som Juan har gjort.

Lösning

Eftersom avståndet från den resade bågen och omkretsens radie är känd, kan den andra formeln appliceras för att känna till den vinkelförskjutning som Juan har gjort. Med hjälp av formeln som beskrivs ovan måste du θ = 35/7 = 5 radianer.

Tredje träning

Om Mario måste i sitt fordon, hälften av ett cirkulärt racingspår, vad är den vinkelförskjutning som Mario har gjort?

Lösning

I denna övning kommer den första formeln att gälla. Eftersom det är känt att Mario har rest hälften av banan, kan det antas att han startade loppet i vinkel 0 ° och när han nådde hälften av omkretsen har han rest 180 °. Därför är svaret 180 ° -0 ° = 180 ° = π radianer.

Fjärde träning

Maria har en cirkulär pool. Din hund springer runt poolen och reser ett avstånd på 18 meter. Om poolradie är 3 meter, vad är den vinklade förskjutningen av Marias husdjur?

Lösning

Eftersom poolen är cirkulär och radien för den är känd kan du fortsätta att använda den andra formeln.

Det är känt att radien är lika med 3 meter, och avståndet som husdjuret reste är lika med 18 meter. Därför är vinkelförskjutningen lika med θ = 18/3 = 6 radianer.

Referenser

1. Katz, D. 2013. Fysik för forskare och ingenjörer. Stiftelser och anslutningar. Cengage Learning.
2. Rex, a. 2011. Fysikens grunder. Pearson.
3. Sears, Zemansky. 2016. Universitetsfysik med modern fysik. 14th. Ed. Volym 1. Pearson.
4. Serway, R., Jewett, J. (2008). Fysik för vetenskap och teknik. Volym 1. 7th. Ed. Cengage Learning.
5. Tipler, s. (2006). Fysik för vetenskap och teknik. 5: e upplagan. Volym 1. Redaktör.