Dynamik i ett partikelsystemexempel, övningar

De Dynamik i ett partikelsystem Det består av tillämpningen av Newtons lagar från rörelsen till en uppsättning partiklar, som kan vara diskret (partiklarna kan räknas) eller vara en del av ett utökat objekt, i detta fall är systemet kontinuerligt.

För att förklara rörelsen av ett partikelsystem är det obekvämt att analysera var och en separat och se vilka krafter som verkar på det. Istället definieras en representativ punkt i uppsättningen, kallad Masscentrum.

Att beskriva Mass Center -rörelsen erbjuder ett mycket framgångsrikt panorama över den globala rörelsen i uppsättningen, gör det också möjligt att tillämpa Newtons lagar analogt när objektet betraktas som en partikel utan dimensioner.

Denna sista modell, kallad partikelmodell, Det är bra att beskriva översättningar och även när det inte är nödvändigt att överväga objektets dimensioner. Men vanliga föremål är storlek och om de också har rotationsrörelse är det nödvändigt att ta hänsyn till de punkter som krafterna tillämpas.

[TOC]

Exempel

Jorden och månen

Jord- och månillustration

En uppsättning diskreta partiklar m₁, m₂, m₃... som så småningom rör sig med avseende på ursprunget till ett koordinatsystem på grund av någon resulterande kraft som verkar på dem är ett bra exempel på partikelsystem.

Jorden kan betraktas som en partikel och månen en annan, sedan utgör båda ett system med 2 partiklar under verkan av solens kraft.

Utökade föremål

En person, ett djur eller något miljöobjekt, kan också betraktas som ett partikelsystem, bara att dessa är så små, att man inte kan räkna en efter en. Detta är ett kontinuerligt system, men med hänsyn till vissa överväganden är behandlingen densamma som för ett diskret system.

Det kan tjäna dig: vad är träningsentalpin? (Med övningar)

Här är detaljerna.

Masscentret för ett partikelsystem

För att starta studien av ett partikelsystem måste du hitta masscentret (CM), vilket är den punkt där systemets hela massa är koncentrerad.

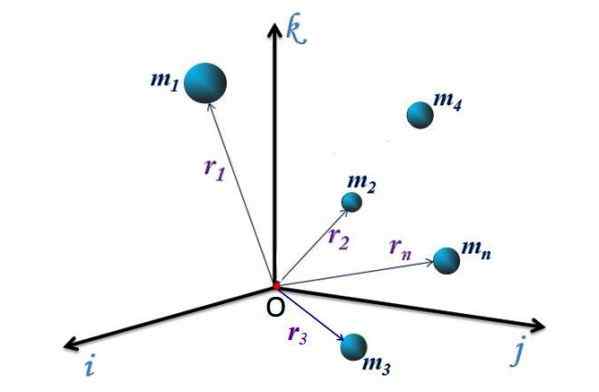
Figur 1. Ett partikelsystem i XYZ -referenssystemet. Källa: f. Zapata.

För det diskreta systemet i figur 1, med n Partiklar, var och en har en positionsvektor riktad från ursprunget eller koordinatsystemet till punkten P (x, y, z) där partikeln är. Dessa vektorer betecknas som r₁, r₂, r₃.. r_n.

CM -koordinater beräknas med följande ekvationer:

Där var och en av massorna i uppsättningen representeras som m₁, m₂, m₃... m_n. Observera att summan ∑ m_Yo Det motsvarar den totala massan m i uppsättningen. Om systemet är kontinuerligt ersätts sammanfattarna med integraler.

Var och en av de vinkelräta adresserna representeras av enhetsvektorerna Yo, J och k, Därför betecknas CM -positionsvektorn r_Centimeter, Det kan uttryckas av:

r_Centimeter = x_Centimeter Yo + och_Centimeter J + z_Centimeter k

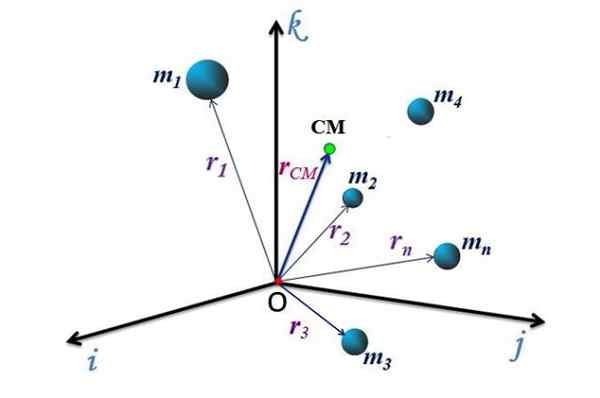figur 2. Masscenterplats för ett partikelsystem. Källa: f. Zapata.

Cm rörelse

När masscentret är känt tillämpas de kända ekvationerna för rörelsen. CM: s hastighet är den första härledda från positionen med avseende på tid:

I detta fall har systemet en total rörelse P som beräknas som produkten av systemets totala massa och masscentrets hastighet:

Det kan tjäna dig: Fysisk bana: Egenskaper, typer, exempel och övningar

P = M ∙v_Centimeter

Alternativt kan den totala mängden system i systemet beräknas direkt:

P = m₁v₁ + m₂v₂ + m₃v₃ +.. . = ∑ m_Yo v_Yo

Medan accelerationen av CM är hastigheten härledd:

Styrka på CM

Krafterna som verkar på ett partikelsystem kan vara:

• Inre krafter på grund av interaktioner mellan samma partiklar.
• Yttre krafter, orsakade av agenter externa till systemet.

Eftersom de inre krafterna presenteras av par, av samma storlek och riktning, men motsatta sinnen, enligt Newtons tredje lag uppfylls det att:

∑ F_int = 0

Därför förändrar de interna krafterna inte helhetens rörelse, men de är mycket viktiga för att bestämma inre energi.

Om systemet är isolerat och det inte finns några yttre krafter, enligt Newtons första lag, är masscentret i vila eller rör sig med enhetlig rektilinär rörelse. Annars upplever centrum för massan en acceleration som ges av:

∑ F_ext = M ∙till_Centimeter

Där m är systemets totala massa. Den tidigare ekvationen kan skrivas så här:

Och det betyder att den yttre kraften motsvarar den tillfälliga variationen i mängden rörelse, ett annat sätt att uttrycka Newtons andra lag och samma som används av den berömda engelska fysikern i sin bok Princip.

Träning löst

Masscentret för ett 2 -partikelsystem är på X -axeln vid ett visst ögonblick, i position X = 2.0 m och rör sig med hastighet 5.0 m/s i samma riktning och positivt. Om en av partiklarna är vid ursprunget och den andra, av massan 0.1 kg, är i vila vid x = 8.0 m, beräkna:

Kan tjäna dig: Diamagnetism: Material, applikationer, exempel

a) Massan på partikeln som är vid ursprunget.

b) mängden systemrörelse

c) Vilken hastighet är partikeln som är vid ursprunget?

Lösning till

Från ekvationen för masscentrumets position:

r_Centimeter = x_Centimeter Yo + och_Centimeter J + z_Centimeter K = 2.0 m Yo

Eftersom CM endast har en X -koordinat används den första trioekvationen som tidigare anges:

Koordinater ersätts nu, om partikeln betecknas vid ursprunget såsom nummer 1 och den andra som nummer 2, är numeriska data:

x₁ = 0 m, x₂ = 8.0 m, m₂ = 0.1 kg, x_Centimeter = 2.0 m

Vistelse:

= 0.3 kg

Lösning B

Mängden systemrörelse beräknas av:

P = M ∙v_Centimeter

Den totala massan M är lika med:

M = 0.3 kg + 0.1 kg = 0.4 kg

Därför:

P = 0.4 kg ∙ 5.0 m/s Yo = 2 kg.Fröken Yo

Lösning C

Av ekvationen för P av ett tvåpartssystem rensar det v₁, Eftersom de andra uppgifterna är kända, eftersom uttalandet säger att partikel 2 är i vila därför:

v₂ = 0 

OCH P Det är helt enkelt som:

P = m₁v₁

v₁ = P / m₁ = 2 kg.Fröken Yo / 0.3 kg = 6.67 m/s Yo

Referenser

1. Hertig universitet. Partiklar. Återhämtat sig från: Webhome.Phy.hertig.Edu.
2. Rex, a. 2011. Fysikens grunder. Pearson.
3. Sears, Zemansky. 2016. Universitetsfysik med modern fysik. 14th. Ed. Volym 1. Pearson.
4. Serway, R., Jewett, J. (2008). Fysik för vetenskap och teknik. Volym 1. 7th. Ed. Cengage Learning.
5. Tipler, s. (2006) Fysik för vetenskap och teknik. 5: e upplagan. Volym 1. Redaktör.