Euklidiskt avståndskoncept, formel, beräkning, exempel

De Euklidisk avstånd Det är ett positivt tal som indikerar den separation som två punkter har i ett utrymme där axiomerna och teoremen för euklidgeometri uppfylls.

Avståndet mellan två punkter A och B i ett euklidiskt utrymme är vektorns längd Ab Tillhör den enda raden som passerar genom dessa punkter.

Figur 1 . Ojämnt euklidiskt utrymme bildat av linjen (OX). Flera punkter på detta utrymme, deras koordinater och avstånd visas. (Förberedd av Ricardo Pérez).

Det utrymme vi uppfattar och där vi flyttar människor är ett tredimensionellt utrymme (3-D), där axiomerna och teoremerna i euklidgeometri är uppfyllda. I detta utrymme finns två dimensionella underområden (planer) och en -dimensionell (rak) (rak) underområden.

Euklidiska utrymmen kan vara av en dimension (1-D), två-dimensioner (2-D), tre dimensioner (3-D) eller N-dimensioner (N-D).

Dessa är punkter i det ena dimensionella utrymmet X som tillhör den orienterade linjen (OX), riktningen från eller till X är den positiva adressen. För att hitta punkterna på denna linje används det kartesiska systemet som består av att tilldela varje punkt i linjen ett nummer.

[TOC]

Formel

Det euklidiska avståndet d (a, b) definieras mellan punkterna a och b, belägen på en linje, såsom kvadratroten på kvadratet för skillnaderna i dess x -koordinater:

D (a, b) = √ ((xb - xa)^2)

Denna definition garanterar att: Avståndet mellan två punkter är alltid ett positivt belopp. Och att avståndet mellan A och B är lika med avståndet mellan B och A.

Figur 1 visar det en -dimensionella euklidiska utrymmet som bildas av linjen (OX) och flera punkter på den linjen. Varje punkt har en koordinat:

Punkt A har XA -koordinat = 2.5, B -koordinaten XB = 4 och punkten C -koordinat XC = -2.5

Det kan tjäna dig: frekvens sannolikhet: koncept, hur det beräknas och exempel

D (a, b) = √ ((4 - 2.5) 2) = 1.5

D (b, a) = √ ((2.5 - 4) 2) = 1.5

D (a, c) = √ ((-2.5 - 2.5) 2) = 5.0

Euklidisk avstånd i två dimensioner

Det två dimensionella euklidutrymmet är ett plan. Punkterna i ett euklidiskt plan möter till exempel axiomerna i euklidgeometri:

- På två punkter passerar en enda linje. 

- Tre punkter på planet bildar en triangel vars inre vinklar alltid lägger till 180º.

- I en rektangel triangel är hypotenusens kvadrat lika med summan av torgarna i benen.

I två dimensioner har en punkt X- och Y -koordinater. 

Till exempel har en punkt P koordinater (XP, YP) ​​och en punkt som koordineras (XQ, YQ).

Euklidiskt avstånd mellan punkt P och Q definieras med följande formel:

D (p, q) = √ ((xq - xp)^2 + (yq - yp)^2)

Det bör noteras att denna formel motsvarar Pythagoras teorem, som visas i figur 2.

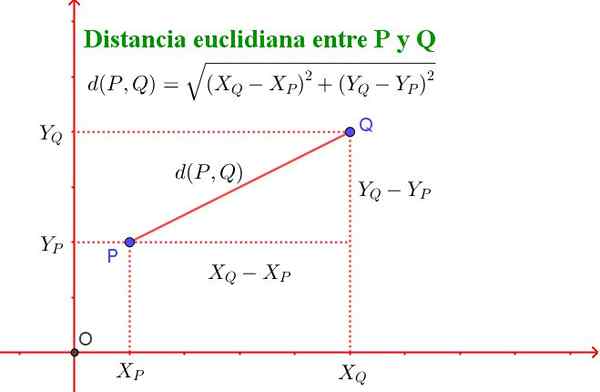figur 2. Avståndet mellan två punkter P och Q i planet möter Pythagoras teorem. (Förberedd av Ricardo Pérez).

Nonuklidiska ytor

Inte alla två dimensionella utrymmen möter euklidisk geometri. Ytan på en sfär är ett två -dimensionellt utrymme.

Vinklarna på en triangel på en sfärisk yta lägger inte till 180º och med detta är Pythagoras teorem inte uppfyllt, därför uppfyller inte en sfärisk yta inte axiomerna i Euclid.

Euklidisk avstånd i n dimensioner

Konceptet med koordinater kan utvidgas till större dimensioner:

- I 2-D-punkt P har koordinater (XP, YP)

- I 3-D en punkt som har koordinater (XQ, YQ, ZQ)

- I 4D-punkt kommer R att koordinater (XR, YR, ZR, WR)

- I N-D kommer en punkt P att ha koordinater (P1, P2, P3, ..., PN)

Kan tjäna dig: staplar graf: egenskaper, vad är det för, exempel

Avståndet mellan två P- och Q-punkter i ett n-dimensionellt euklidiskt utrymme beräknas med följande formel:

D (p, q) = √ ((q1 - p1)^2 +(q2 - p2)^2 +... +(qn - pn)^2)

Den geometriska platsen för alla punkter som i ett n-dimensionellt euklidiskt utrymme som likvidister från en annan fast P-punkt (centrum) bildar en n-dimensionell hypersfera.

Hur man beräknar det euklidiska avståndet

Nedan är avståndet mellan två punkter belägna i Euklidiska tre -dimensionella utrymmet beräknas.

Anta punkt A av kartesiska koordinater X, Y, Z ges av A :( 2, 3, 1) och punkt B för koordinater B :( -3, 2, 2).

Du vill bestämma avståndet mellan dessa punkter, för vilket det allmänna förhållandet används:

D (a, b) = √ ((-3 - 2) 2 + (2 - 3) 2 + (2 - 1) 2) = √ ((-5) 2 + (-1) 2 + (1) 2 )

D (a, b) = √ (25 + 1 + 1) = √ (27) = √ (9 *3) = 3 √ (3) = 5.196

Exempel

Det finns två punkter P och Q.  P -punkten för kartesiska koordinater x, y, z ges av p :( 2, 3, 1) och punkten q för koordinater Q :( -3, 2, 1).

Det uppmanas att hitta koordinaterna för mittpunkten M i [PQ] -segmentet som ansluter de två punkterna. 

Lösning:

Det antas att den okända punkten M har koordinater (x, y, z).

Eftersom m är en genomsnittlig punkt för [pq] måste det uppfyllas att d (p, m) = d (q, m), så det måste också uppfyllas d (p, m)^2 = d (q, m)^ 2:

(X - 2)^2 + (y - 3)^2 + (z - 1)^2 = (x - (-3))^2 + (y - 2)^2 + (z - 1)^2

Liksom i detta fall är den tredje terminen densamma i de två medlemmarna förenklas det tidigare uttrycket för:

Kan tjäna dig: absolut konstant

(X - 2)^2 + (y - 3)^2 = (x + 3)^2 + (y - 2)^2 

Det finns då en ekvation med två okända x och y. En annan ekvation krävs för att lösa problemet.

Punkt M tillhör linjen som passerar genom P- och Q -punkterna, som vi kan beräkna enligt följande:

Först är regissörens vektor Pq av linjen: Pq = = .

Sedan P.m = Op + till Pq, var Op Det är vektorpositionen för punkt P och till Det är en parameter som tillhör riktiga siffror. 

Den föregående ekvationen är känd som vektorekvationen för linjen, som i kartesiska koordinater antar enligt följande:

= + a =

Lika motsvarande komponenter är:

X - 2 = 2 - 5 a; Och - 3 = 3 -a; Z - 1 = 0

Det vill säga att x = 4 - 5a, y = 6 - a, slutligen z = 1.

Det ersätts i det kvadratiska uttrycket som relaterar x till y:

(4 - 5a - 2)^2 + (6 - a - 3)^2 = (4 - 5a + 3)^2 + (6 - a - 2)^2

Det är förenklat:

(2 - 5a)^2 + (3 -a)^2 = (7 - 5a)^2 + (4 - a)^2

Utvecklas nu:

4 + 25 a^2 - 20a + 9 + a^2 - 6a = 49 + 25 a^2 - 70a + 16 + a^2 - 8a

Det är förenklat och avbryter liknande villkor i båda medlemmarna:

4 - 20A + 9 - 6A = 49 - 70A + 16 - 8A

Parameter A:

52 a = 49 + 16 - 4 - 9 = 52 vilket resulterar i att a = 1.

Det vill säga att x = 4 - 5, y = 6 - 1, slutligen z = 1.

Slutligen erhåller vi de kartesiska koordinaterna för Segmentets mittpunkt M [PQ]:

M: (-1, 5, 1).

Referenser

1. Lehmann c. (1972) Analytisk geometri. Utea.
2. Superprof. Avstånd mellan två poäng. Återhämtat sig från: superprof.är
3. Unk. Avstånd mellan relaterade sublinear sorter. Återhämtat sig från: Prometheus.Matem.Unk.MX/
4. Wikipedia. Euklidisk avstånd. Återhämtad från: är.Wikipedia.com
5. Wikipedia. Euklidiskt utrymme. Återhämtad från: är.Wikipedia.com