Diskreta distributioner
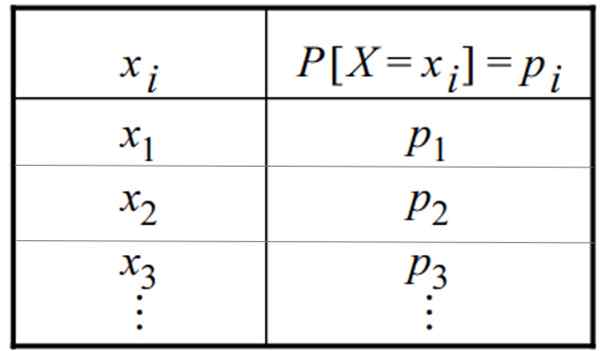
- 2734
- 143
- Johan Eriksson
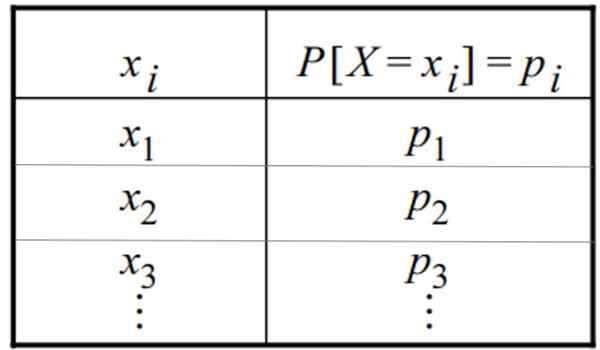 Tabell över en diskret sannolikhetsfördelning. Källa: f. Zapata
Tabell över en diskret sannolikhetsfördelning. Källa: f. Zapata Vad är en diskret distribution?
En diskret distribution av sannolikheter är en funktion f (xYo) som tilldelar varje värde på en diskret variabel: x1, x2, x3,... xYo, en viss förekomst av förekomst p (x = xYo). Denna funktion är också känd som "sannolikhetsmassafunktion".
Den diskreta sannolikhetsfördelningen kan ges i form av en tabell eller en grafik. En tabell har denna allmänna form, där variabeln visas i en kolumn och dess respektive sannolikhet i den andra:
Sannolikhetsmassafunktioner delar följande allmänna egenskaper:
- Sannolikheten pYo av alla X -händelserYo Det är mellan 0 och 1, till och med några av dessa begränsningsvärden: 0 ≤ x ≤ 1.
- P (x = xYo) = PYo Ta bara positiva värden därför: P (x = xYo) ≥ 0.
- Det är sant att ∑ p (xYo) = 1 för alla möjliga värden på x.
En sannolikhetsfördelning beskriver beteendet hos en befolkning, beskrivet av dess parametrar: den genomsnittliga μ, variansen σ2 och standardavvikelsen S = σ σ2.
Därefter beskrivs de mest anmärkningsvärda diskreta distributionerna kort:
Jämn fördelning
Det är den enklaste diskreta fördelningen av alla. I den kan variabeln ta "n" diskreta värden: x1, x2, x3,... xYo, Alla med samma sannolikhet. I detta fall ges distributionen av:
Binomial distribution
Det gäller upplevelser med endast två möjliga och ömsesidigt exklusiva resultat, som vanligtvis kallas "framgång" och "misslyckande", betecknade som E respektive F. Det faktum att en händelse kallas "framgång", betyder inte nödvändigtvis att det är bra, det är snarare en godtycklig beteckning.
Sannolikheten för framgång p (e) i "n" repetitioner, betecknas som p, och den för misslyckande p (f) som q = 1 - p.
Om "x" representerar ett visst antal framgångar i "n" oberoende försök, är det sant att: 0 ≤ x ≤ n. Och sannolikheten för händelse P (x) beräknas genom följande formel:
Det kan tjäna dig: kvadratcentimeter till kvadratmeter (cm² till m²)Där x = 0, 1, 2, 3 ..., n och symbolen (!) betyder "factorial":
x! = x ∙ (x - 1) ∙ (x - 2) ∙ (x - 3) ... 1
0! = 1
Poisson Distribution
I denna distribution indikerar den slumpmässiga variabeln X hur många gånger en händelse som inträffar i något intervall, vilket kan vara av tid, avstånd eller annat. Händelsens händelser är slumpmässiga, oberoende och fördelas jämnt under hela intervallet.
När dessa förhållanden beräknas sannolikheten, som beror på genomsnittet av μ -händelser och antalet Euler eller antal "E", av:
Chanserna för händelser med denna distribution är små, så det kallas "lagen i sällsynta fall".
Binomial distributionsmetod
Poissons distribution fungerar som en metod för binomial distribution när N är stor (n≥ 100) och P är liten (NP ≤ 10). I detta fall beräknas det genomsnittliga μ som:
μ = n ∙ p
Hypergeometrisk distribution
Det används när sannolikheterna inte är oberoende, det vill säga efter att ha genomfört experimentet är förhållandena inte desamma igen. Detta är vad som händer när man extraherar prover utan ersättning från en befolkning, så att binomialfördelningen inte längre kan användas.
Om befolkningen består av två typer av objekt som skiljer sig från och B, och vid slumpmässiga objekt och utan ersättning, är sannolikheten för att få X -objekt av typ A:
Där A och B är respektive mängder föremål av varje typ, närvarande i befolkningen.
Men om befolkningen är mycket stor, även om det inte finns någon ersättning, är det svårt för samma element att väljas mer än en gång, så båda distributionerna: binomial och hypergeometriska, ger liknande resultat.
Kan tjäna dig: kuber skillnad: formler, ekvationer, exempel, övningarExempel
Mynt lanserar
CO -lansering är mycket illustrativa exempel:
-Lanseringen av en ärlig valuta och få ett ansikte. Det är känt att 1 ansikte har ½ sannolikhet för att lämna och korset (0 ansikte), samma. Distributionen visas i denna tabell:
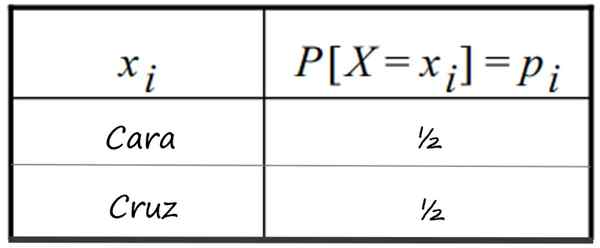 Diskret sannolikhetsfördelningstabell som följer lanseringen av 1 ärlig valuta. Källa: f. Zapata
Diskret sannolikhetsfördelningstabell som följer lanseringen av 1 ärlig valuta. Källa: f. Zapata -Det samtidiga skottet av två Ärliga mynt och möjliga ansikten som kan erhållas.
 Diskret sannolikhetsfördelningstabell som följer lanseringen av två ärliga valuta, i syfte att få något ansikte eller inte. Källa: f. Zapata
Diskret sannolikhetsfördelningstabell som följer lanseringen av två ärliga valuta, i syfte att få något ansikte eller inte. Källa: f. Zapata Variabler med enhetlig distribution
-Valet av ett heltal som är jämnt eller udda: var och en är sannolikhet som är lika med ½ att väljs inom uppsättningen av hela siffror.
-Lanseringen av en ärlig tärning. I det här fallet finns det 6 numrerade ansikten och var och en har samma sannolikhet att lämna: 1/6.
-Valet av ett ämne att ta en tentamen, valt mellan N -frågor, om alla är lika troliga.
Variabler med binomial distribution
-Antal ansikten som kommer ut genom att lansera ett ärligt mynt.
-Av en befolkning på 250 familjer är antalet som har två barn.
-Mängden rosenträ som överlever, efter en trädgårdsmästare 20 rosales i en trädgård.
-Av en studie med 50 patienter, antalet som presenterade en negativ reaktion på ett läkemedel.
-Antalet studenter som godkänts i en sannolikhetsexamen, av en grupp som består av 100 studenter.
Variabler med Poisson -distribution
-Antal samtal per minut till Callcenter Av ett företag.
-Antal stora jordbävningar per år för ett specifikt geografiskt område.
-Antalet tornadon som påverkade en viss region under det senaste året.
-Antal träd infekterade med en svamp, per kvadratisk skogshektar.
Variabler med hypergeometrisk distribution
-Framgångar för siffror eller vinnande kombinationer inom spel.
Kan tjäna dig: samtidiga vektorer: egenskaper, exempel och övningar-Urval av ett visst antal kvinnor eller män i ett prov av n fiskar av en fiskskål.
Löst övningar
Övning 1
En studie fastställde att 54% av dem använder dem i klassen eller möten av slumpmässigt välj vuxna som har smartphones. Du vill hitta sannolikheten för att slumpmässigt välja 8 personer med smartphone, exakt 6 av dem använder dem i klassen eller möten.
Lösning
Detta experiment överensstämmer med ett binomialt experiment, eftersom resultatet är binärt: en person tar telefonen i klassen eller inte tar ut den. Det faktum att personen använder telefonen som är i klassen kan kallas framgång och ett misslyckande om det inte gör det (innan det förklarades att detta val är helt godtyckligt).
I så fall: p = 0.54 och Q = 1- 0.54 = 0.46.
Eftersom 8 personer är slumpmässigt valda, då n = 8 och värdet på x är 6, är de nödvändiga värdena tillgängliga för att ersätta dem i binomialfördelningsformeln:
Övning 2
Under ett nyligen år registrerade en klinik 4221 födelser. Bestäm sannolikheten för att det finns 15 födelser på 1 dag med denna unika data. Är denna händelse sällsynt?
Lösning
Poisson -distribution används, eftersom det uppmanas att bestämma sannolikheten för förekomst av en händelse som inträffar i ett tidsintervall. I detta fall är variabeln mängden födelser och intervallet är en dag.
Poisson -distributionsformeln behöver den genomsnittliga födelsen per dag, vilket lätt beräknas:
Därför är sannolikheten för x = 15 födelser/dag:
Resultatet kan uttryckas i procent för tydlighet: 6.42% troligtvis att exakt 15 födelser på någon dag inträffar. Evenemanget är osannolikt, även om det inte är omöjligt.


=\frac1n)
=\fracn!\left&space;(&space;n-x&space;\right&space;)!\cdot&space;x!\cdot\:p^x\cdot&space;q^n-x)
=\frac\mu&space;^x\cdot&space;e^-\mu&space;x!)
=\fracA!\left&space;(A-x&space;\right&space;)!\cdot&space;x!\cdot&space;\fracB!\left&space;(B-n+x&space;\right&space;)!\cdot&space;\left&space;(n-x&space;\right&space;)!\div&space;\frac\left&space;(A+B&space;\right&space;)!\left&space;(A+B-n&space;\right&space;)!\cdot&space;n!)
=\frac8!\left&space;(8-6&space;\right&space;)!\times&space;6!\times&space;0.54^6\times&space;0.46^\left&space;(8-6&space;\right&space;)=\frac8!2!\times&space;6!\times&space;0.54^6\times&space;0.46^2=0.147)

=\frac11.56^15\times&space;e^-11.5615!=0.0642)