Dopplereffektbeskrivning, formler, fall, exempel

han Dopplereffekt Det är ett fysiskt fenomen som inträffar när mottagaren och källan till vågor har relativ rörelse, vilket orsakar en förändring i mottagarens frekvens med avseende på källans frekvens.

Hans namn beror på den österrikiska fysikern Christian Doppler (1803-1853), som beskrev och förklarade detta fenomen 1842, medan han presenterade ett verk på färgen på dubbla stjärnor, i en naturkongress i Prag, nuvarande tjeckiska republik.

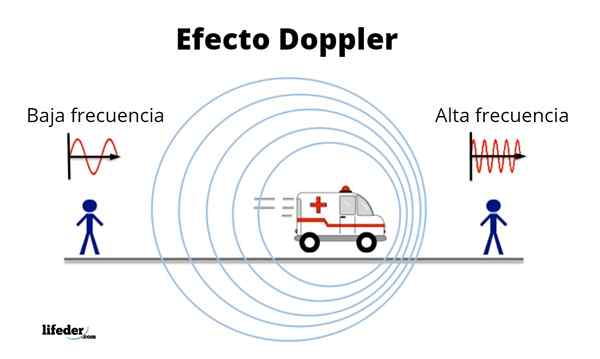
Illustration av Doppler -effekten

[TOC]

Där Doppler -effekten presenteras?

Figuren illustrerar en källa till vågor som rör sig från vänster till höger. En observatör före källan uppfattar korta våglängder och det motsatta för en observatör bakom. Källa: Wikimedia Commons.

Doppler -effekten presenteras i alla typer av vågor, från det lysande till ljudet, förutsatt att källan och mottagaren rör sig på varandra. Och det är mycket mer anmärkningsvärt när den relativa hastigheten mellan källan och mottagaren är jämförbar med hastigheten för utbredningshastigheten.

Anta en harmonisk våg, som är en svängning som går framåt i rymden. Ovängningen upprepas med regelbundna tidsintervall, den här gången är termen och hans omvända frekvensen, Det är antalet svängningar per tidsenhet. 

När avståndet mellan källan till den harmoniska vågen och mottagaren förblir fixerad uppfattar mottagaren samma källfrekvens, det vill säga det registrerar samma antal pulser per tidsenhet som källan. 

Men när mottagaren närmar sig källan med fast hastighet, kommer pulserna oftare. Och det motsatta inträffar när mottagaren rör sig bort från fast hastighet från källan: vågpulser uppfattas med en lägre frekvens.

Doppler -effektbeskrivning

För att förstå varför detta fenomen inträffar kommer vi att använda en analogi: två personer som spelar bollar. Pitcher får dem att rulla i en rak linje på marken mot partner, som plockar upp dem.

Om personen som lanserar skickar en boll varje sekund kommer den som samlar dem, om den förblir fast, att fånga en boll varje sekund. Allt bra hittills, eftersom det förväntas.

Rörelsesmottagaren

Anta nu att personen som fångar bollarna är på ett skateboard och bestämmer sig för att närma sig kannan med konstant hastighet. I det här fallet, när du kommer att träffa bollarna, kommer du att ha mindre än en sekund mellan en boll och följande.

Därför verkar mottagaren vara mer än en boll per sekund, det vill säga frekvensen som de når hans hand ökade. 

Det kan tjäna dig: fysik under grekerna (Antige Grekland)

Det motsatta skulle hända om den mottagande personen beslutade att flytta bort från emittenten, det vill säga bollens ankomsttid skulle öka med den därmed minskade frekvensen som bollarna anländer.

Formler

Frekvensändringen som beskrivs i föregående avsnitt kan erhållas från följande formel:

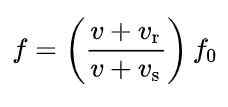
Här:

-F_antingen Det är källans frekvens.
-F är den uppenbara frekvensen i mottagaren.
-v är hastigheten (v> 0) för utbredning av vågen i mitten.
-v_r är mottagarens hastighet med avseende på miljön och
-v_s är hastigheten på källan relaterad till mediet.

Observera att v_r Det är positivt om mottagaren närmar sig källan och negativt på annat sätt. Å andra sidan, v_s Det är positivt om källan rör sig bort från mottagaren och negativ när den närmar sig.

Kort sagt, om källan och observatörens tillvägagångssätt ökar frekvensen och om de flyttar bort minskar. Det motsatta inträffar med den uppenbara våglängden i mottagaren (se övning 1).

Fall där Doppler -effekten finns

Källhastighet och mottagare mycket lägre än vågen

Det händer ofta att vågens hastighet är mycket större än hastigheten med vilken källan eller rörelsens hastighet rör sig.

I detta fall kan formeln approximeras på ett sådant sätt att den skrivs baserat på mottagarens relativa hastighet (observatör) med avseende på källorna (erna).

I detta fall skulle formeln vara så här:

F = [1 + (VRS/V)] ⋅F_antingen

Där v_Rs = v_r - v_s.

När v_Rs Det är positivt (de närmar sig), frekvensen f är större än f_antingen, När det är negativt (de flyttar bort) är F mindre än F_antingen.

Relativ hastighetsformningsvinkel med den relativa positionen

Den föregående formeln gäller endast för det fall att källan närmar sig (eller flyttar bort) direkt från observatören.

I händelse av att källan flyttar in efter en tvärgående väg är det nödvändigt.

I det här fallet måste vi ansöka:

F = [1 + (v_Rs ⋅ cos (θ) / v)] ⋅ f_antingen

Återigen, en v_Rs Positiva tecken tilldelas om mottagaren och källan närmar sig och negativ om den inträffar tvärtom.

Doppler Effect Exempel

Ett dagligt exempel är sirenen i en ambulans eller patrull. När du närmar oss är det mer akut och när det rör sig är det mer allvarligt, särskilt skillnaden hörs vid tidpunkten för maximal tillvägagångssätt.

Det kan tjäna dig: Fysisk bana: Egenskaper, typer, exempel och övningar

En annan situation som förklaras av Doppler -effekten är förskjutningen av stjärnans spektrala linjer mot blått eller rött, om de närmar sig oss eller om de flyttar bort. Detta kan inte märkas med blotta ögat, men med ett instrument som heter spektrometer.

Ansökningar

Doppler -effekten har många praktiska applikationer, vissa listas nedan:

Radar

Radarna mäter avståndet och hastigheten med vilket objekten som upptäcks av den rör sig och baseras exakt på Doppler -effekten.

Radaren avger en våg mot det objekt som du vill upptäcka, då reflekteras den vågen tillbaka. Den tid det tar för en puls att gå och returnerar tjänar till att bestämma avståndet till vilket objektet är. Och frekvensändringen i den reflekterade signalen gör det möjligt att veta om objektet i fråga rör sig bort eller närmar sig när radar och hur snabbt.

Eftersom radarvågen går och återvänder finns det en dubbel doppler -effekt. I detta fall är formeln som gör det möjligt att bestämma objektets hastighet med avseende på radaren:

V_eller = ½ c ⋅ (Δf / f_antingen)

Var:
-V_eller Det är objektets hastighet med avseende på radaren.
-c Den utsända vågens hastighet och reflekteras sedan.
-F_antingen Radarutsläppsfrekvensen.
-Δf Frekvensförskjutningen, det vill säga F - F_antingen.

Astronomi

Tack vare Doppler -effekten har det fastställts att universum expanderar, eftersom ljusspektrumet som släpps ut av avlägsna galaxer förflyttas mot rött (en frekvensminskning).

Å andra sidan är det också känt att avgångshastigheten växer i den utsträckning att de observerade galaxerna är mer avlägsna.

Annars förekommer det med vissa galaxer i den lokala gruppen, det vill säga grannarna till vår mjölkiga väg.

Till exempel har vår närmaste granne, Andromeda Galaxy en blå stigning (det vill säga en ökning av frekvensen) som indikerar att vi närmar oss oss.

Doppler ultraljud

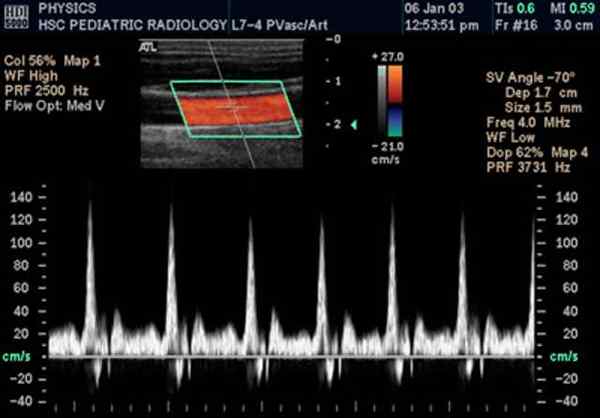Doppler ultraljud av karotisartären. Källa: Wikimedia Commons.

Det är en variant av det traditionella ekosonogrammet, där att dra nytta av Doppler -effekten hastigheten på blodflödet i vener och artärer mäts.

Övningar

Övning 1 

Sirenen i en ambulans har en frekvens är 300 Hz. Att veta att ljudets hastighet i luften är 340 m/s, bestäm ljudets våglängd i följande fall:

Det kan tjäna dig: kalibreringskurva: Vad är det för, hur man gör det, exempel

a) När ambulansen är i vila.

b) Om du närmar dig 108 km/h 

c) genom att flytta bort med samma hastighet.

Lösning till

Det finns ingen Doppler -effekt eftersom både emittenten och källan är i vila.

För att bestämma ljudets våglängd, förhållandet mellan frekvensen för f -änden f, våglängden λ för källan och ljudets hastighet v:

v = f_antingen⋅λ.

Därifrån följer det:

λ = v / f_antingen.

Därför är våglängden:

λ = (340 m/s)/(300 1/s) = 1,13 m.

Lösning B

Mottagaren betraktas i vila, det vill säga_r = 0. Emitteren är sirenen som rör sig med ambulansens snabbhet:

v_s = (108/3,6) m/s = 30 m/s.

Den uppenbara frekvensen F ges av förhållandet:

f = f_antingen⋅ [(V + V_r)/(V + v_s)]]

Tillämpning av denna formel erhålls:

F = 300 Hz ⋅ [(340 + 0)/(340 - 30)] = 329 Hz.

Våglängden på mottagaren kommer att vara:

λ_r= v / f = (340 m / s) / (329 1 / s) = 1,03 m.

Lösning C

Det är löst på liknande sätt:

F = 300 Hz ⋅ (340 + 0)/(340 + 30) = 276 Hz.

Våglängden på mottagaren kommer att vara:

λ_r = v / f = (340 m / s) / (276 1 / s) = 1,23 m.

Det dras slutsatsen att vågfronter har en separation av 1,03 m när sirenen närmar sig och 1,23 m när den rör sig bort.

Övning 2

En karakteristisk linje i väteutsläppsspektrumet är 656 nm, men när man observerar en galax ser man att samma linje förflyttas och 660 nm märken, det vill säga den har en 4 nm röd skift.

Eftersom det finns en ökning av våglängden, vet vi att galaxen rör sig bort. Vad är din hastighet? 

Lösning

Kvoten mellan förskjutningen av våglängden och vilande våglängd är lika med kvoten mellan galaxens hastighet och ljusets hastighet (300.000 km/s). Så:

4/656 = 0.006

Därför rör sig galaxen bort vid 0.006 gånger ljusets hastighet, det vill säga 1800 km/s.

Referenser

1. Alonso - Finn. Volymfysik.2. 1970. Inter -American Education Fund, s.TILL. 
2. Baranek, L. 1969. Akustik. 2: a. Utgåva. McGraw Hill.
3. Griffiths G. Linjära och olinjära vågor. Återhämtat sig från: Scholarpedia.org.
4. Whitham G.B. 1999. Linjära och olinjära vågor. Wiley. 
5. Wikiwaves. Olinjära vågor. Återhämtat sig från: wikiwaves.org
6. Wikipedia. Dopplereffekt. Återhämtad från: är.Wikipedia.com