ENEGON EGENSKAPER, Hur man gör en ENEGON, exempel

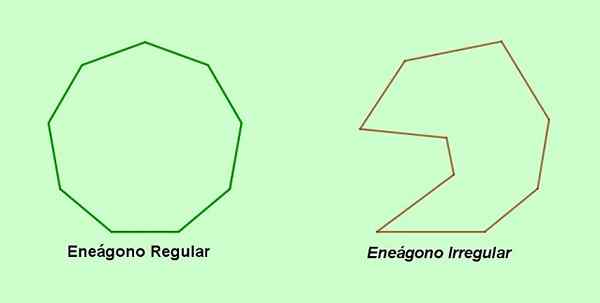
En Enegon Det är en polygon på nio sidor och nio vertikaler, som kan vara regelbundna eller inte. Enegon -valören kommer från det grekiska och består av de grekiska orden Ennea (nio och Gonon (vinkel).

Ett alternativt namn för den nio -sidade polygonen är ett ord som inte är ord som kommer från latin nonus (nio och Gonon (vertex). Å andra sidan, om sidorna eller vinklarna på Enegon är ojämlika för varandra, finns det då a oregelbunden enegon. Om tvärtom, de nio sidorna och de nio vinklarna i ENEGON är lika, är det en vanlig ENEGON.

Figur 1. Regelbunden ENEGON och oregelbunden ENEGON. (Egen utarbetande)

[TOC]

Enegon -egenskaper

För en polygon av N -sidor är summan av dess inre vinklar:

(N - 2) * 180º

I ENEGON skulle det vara n = 9, så summan av dess inre vinklar är:

SA = (9 - 2) * 180º = 7 * 180º = 1260º

I någon polygon är antalet diagonaler:

D = n (n - 3) / 2 och i fallet med Enegon, som n = 9, måste du d = 27.

Vanlig ENEGON

I ENEGON eller vanliga nonagon.

Det är då nödvändigt att mäta de inre vinklarna på en ENEGON är 1260º / 9 = 140º.

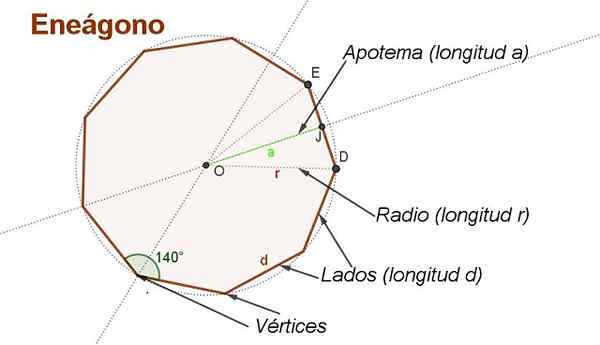figur 2. Apotem, radio, sidor, vinklar och vertikaler för en vanlig ENEGON. (Egen utarbetande)

Att härleda formeln för området för en vanlig ENEGON på sidan d Det är bekvämt att göra några hjälpkonstruktioner, till exempel de som visas i figur 2.

Centret är ANTINGEN Ritar mediatrikerna från två angränsande sidor. Centrum ANTINGEN Vertikalers equidista.

En radie av längd r Det är segmentet som går från mitten ANTINGEN På ett toppe av ENEGON. Radioapparater visas i figur 2 Va och Oe av längd r.

Kan tjäna dig: symmetri

Apotem är det segment som går från mitten till mittpunkten på ena sidan av ENEGON. Till exempel Oj Det är en apotem vars längd är till.

Område av en enegon känd sida och apotem

Vi betraktar triangeln ODE Från figur 2. Området för denna triangel är produkten från dess bas AV med höjd Oj dividerat med 2:

Område ODE = (Från * oj) / 2 = (D * a) / 2

Eftersom det finns 9 trianglar av samma område i ENEGON, dras det då att området med samma är:

Enegon = (9/2) (d * a)

Området i en känd enegon

Om bara längden på Enegon är känd, är det då nödvändigt att hitta den apotemlängden för att kunna tillämpa formeln för föregående avsnitt.

Vi betraktar triangeln Oje Rektangel J (Se figur 2). Om det vridmoment trigonometriska förhållandet tillämpas, erhålls det:

så(∡Oej) = Oj / T.ex.

Vinkeln ∡oej = 140º / 2 = 70º, för att vara Eo Bisektor av den inre vinkeln i Enegon.

Förutom, Oj Det är apotem av längd till.

Då som J Det är en mittpunkt på Ed Det följer att Ex = D/2.

Att ersätta ovanstående värden i tangentens förhållande är:

Tan (70º) = A / (d / 2).

Nu rensar vi apotemlängden:

A = (d/2) Solbränna (70º).

Det föregående resultatet ersätts i formeln för området för att få:

Enegon = (9/2) (D * A) = (9/2)( D * (d/2) Solbränna (70º))

Slutligen finns det formeln som gör det möjligt att erhålla det vanliga ENEGON -området om bara längden är känd d av dess sidor:

Enegon = (9/4) D² Tan (70º) = 6,1818 D²

Omkrets av den vanliga ENEGON kända sin sida

Omkretsen av en polygon är summan av dess sidor. När det gäller ENEGON, som var och en av sidorna mäter den en längd d, Dess omkrets är summan nio gånger d, det vill säga:

Kan tjäna dig: polynomiska ekvationer

Omkrets = 9 d

Omkretsen av Enegon känd sin radio

Med tanke på triangeln Oje Rektangel J (Se figur 2), den trigonometriska orsaken till att COSEN tillämpas:

cos (∡Oej) = T.ex / Oe = (d / 2) / r

Var erhålls du:

D = 2r cos (70º)

Genom att ersätta detta resultat erhålls omkretsformeln som en funktion av ENEGON -radien:

Omkrets = 9 d = 18 r cos (70º) = 6 1564 r

Hur man gör en vanlig ENEGON

1- För att bygga en vanlig ENEGON, med regel och kompass, är den baserad på omkretsen c som omskriver ENEGON. (Se figur 3)

2- Två vinkelräta linjer dras genom mitten eller omkretsen. Sedan är korsningar A och B i en av linjerna markerade med omkretsen.

3- med kompassen, gör centrum i avlyssningen B och öppnar lika med radien bo.

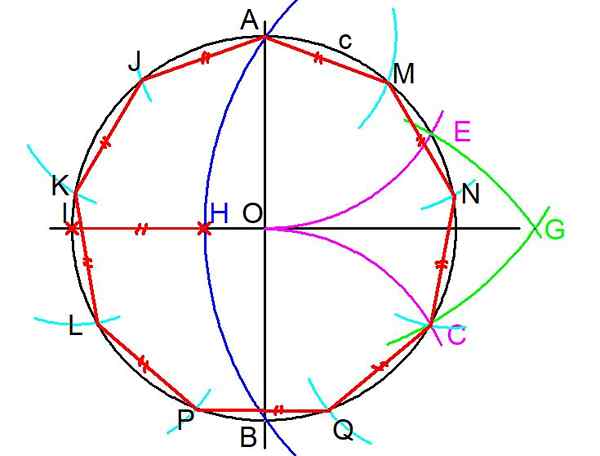Figur 3. Steg för att bygga en vanlig ENEGON. (Egen utarbetande)

4- Det föregående steget upprepas men gör ett centrum i A och Radio Ao en båge dras som avlyssnar till omkretsen C vid punkt E.

5- Med AC-öppning och mitt i en omkretsbåge ritas. På samma sätt med öppning BE och Center B dras en annan båge. Korsningen mellan dessa två bågar markeras som en g.

6- Skapa centrum i G och med GA som öppnar en båge dras som avlyssnar den sekundära axeln (horisontellt i detta fall) vid punkt H. Korsningen mellan den sekundära axeln är markerad med den ursprungliga omkretsen C som jag.

7- Längden på IH-segmentet är lika med längden D på sidan av ENEGON.

8- Med en kompassöppning IH = D är mittbågarna successivt till Radio AJ, Centro J Radio AK, KL Radio KL och Centro L Radio LP.

Det kan tjäna dig: linjära transformationer: egenskaper, vad är användning, typer, exempel

9- På liknande sätt, med början från A och på höger sida, dras Radio Arcos IH = D på de ursprungliga omkretsen C-poäng M, N, C och Q.

10- Slutligen dras segmenten AJ, JK, KL, LP, AM, MN, NC, CQ och slutligen PB.

Det bör noteras att konstruktionsmetoden inte är helt exakt, eftersom det kan verifieras att den sista PB -sidan är 0,7% längre än de andra sidorna. Hittills är en konstruktionsmetod för konstruktion och kompass inte känd som är 100% exakt.

Exempel

Några exempel som löses kommer att behandlas nedan.

Exempel 1

Du vill bygga en vanlig ENEGON vars sidor mäter 2 cm. Vilken radio bör omkretsen som omskriver den, så att vid tillämpning av den tidigare beskrivna konstruktionen erhålls det önskade resultatet?

Lösning:

I ett tidigare avsnitt härleddes formeln som relaterar radien för den omskrivna omkretsen med D -regelbundet Dégon:

D = 2r cos (70º)

Rensa R från det tidigare uttrycket vi har:

R = d / (2 cos (70º)) = 1 4619 * D

Ersättning av värdet d = 2 cm i föregående formel A 2,92 cm radie erhålls.

Exempel 2

Hur mycket är området för en vanlig 2 cm sida enegon?

Lösning:

För att svara på den här frågan måste du hänvisa till formeln, tidigare demonstrerat, vilket gör att du kan hitta området för en enegon som är känd längden D på sin sida:

Enegon = (9/4) D² Tan (70º) = 6,1818 D²

Att ersätta D för dess värde på 2 cm i den främre formeln erhålls:

Enegon = 24,72 cm

Referenser

1. C. OCH. TILL. (2003). Geometrielement: med övningar och kompassgeometri. University of Medellin.
2. Campos, f., Cerecedo, f. J. (2014). Matematik 2. Patria Redaktionsgrupp.
3. Freed, K. (2007). Upptäck polygoner. Utbildningsföretag.
4. Hendrik, V. (2013). Generaliserade polygoner. Birkhäuser.
5. Iriger. (s.F.). Matematik första termin Tacaná. Iriger.
6. Jr. Geometri. (2014). Polygoner. Lulu Press, Inc.
7. Miller, Heeren och Hornsby. (2006). Matematik: Resonemang och applikationer (tionde upplagan). Pearson Education.
8. Patiño, m. (2006). Matematik 5. Redaktionell progreso.