Gravitationsenergiformler, egenskaper, applikationer, övningar

De Gravitationsenergi Det är den som har ett massivt objekt när det är nedsänkt i gravitationsfältet som produceras av ett annat. Några exempel på föremål med gravitationsenergi är: äpplet i trädet, äpplet faller, månen som kretsar runt jorden och jorden som kretsar runt solen.

Isaac Newton (1642-1727) var den första som insåg att tyngdkraften är ett universellt fenomen och att varje objekt med massa producerar i sin miljö ett fält som kan producera en kraft på en annan.

Figur 1. Månen som kretsar runt jorden har gravitationsenergi. Källa: Pixabay

[TOC]

Formler och ekvationer

Kraften som hänvisas till i Newton är känd som gravitationskraft och ger energi till det föremål som den verkar. Newton formulerade den universella gravitationslagen på följande sätt:

"Var två specifika massobjekt M1 respektive M2, var och en utövar på den andra en attraktionskraft som är proportionell mot produkten från deras massor och omvänt proportionell mot kvadratet på avståndet som skiljer dem.".

I det föregående uttrycket, F Det är kraften i gravitation attraktion som objekt 1 utövar på objekt 2 (eller vice versa), M1 och m2 De respektive massorna av föremål och R är avståndet som skiljer föremål. G Det är en konstant av proportionalitet som kallas gravitationskonstanten.

Gravitationsenergi ELLER associerad med gravitationskraft F är:

Notera närvaron av ett negativt tecken, vilket innebär att om separationen mellan objekt är begränsad är dess gravitationsenergi negativ. Men om separationen tenderar att oändligheten är gravitationsenergin noll.

Ett objekt som är nedsänkt i ett gravitationsfält har gravitationspotential energi ELLER och kinetisk energi K. Om det inte finns några andra interaktioner, eller de är av försumbar intensitet, den totala energin OCH Av detta objekt är summan av dess gravitationsenergi plus dess kinetiska energi:

E = k + u

Om ett objekt är i ett gravitationsfält och andra dissipativa krafter inte finns, såsom friktion eller luftmotstånd, är den totala energin OCH Det är ett belopp som förblir konstant under rörelse.

Egenskaper för gravitationsenergi

- Ett objekt har gravitationspotential energi om det bara är i närvaro av gravitationsfältet som produceras av ett annat.

- Gravitationsenergin mellan två objekt växer när separationsavståndet mellan dem är större.

- Det arbete som utförs av gravitationskraften är lika och strider mot variationen i gravitationsenergin i den slutliga positionen med avseende på den för dess initiala position.

Det kan tjäna dig: vad är partikelns balans? (Med exempel)

- Om en kropp endast utsätts för tyngdkraften, är variationen i dess gravitationsenergi lika och strider mot variationen i dess kinetiska energi.

- Den potentiella energin i ett massobjekt m på en höjd h När det gäller jordens yta är Mgh gånger större än den potentiella energin på ytan, vara g Acceleration av tyngdkraften för höjder h Mycket lägre än den markbundna radien.

Fält- och gravitationspotential

Gravitationsfältet g Det definieras som gravitationskraft F per massa. Det bestäms genom att placera en testpartikel vid varje punkt i rymden och beräkna kvoten mellan kraften som verkar på testpartikeln dividerat med värdet på dess massa:

g = F / m

Gravitationspotentialen V för ett massobjekt M som gravitationspotentialenergi för det objektet dividerat med sin egen massa definieras.

Fördelen med denna definition är att gravitationspotentialen endast beror på gravitationsfältet, så att när potentialen är känd V, Gravitationsenergi ELLER av ett massobjekt m är:

U = m.V 

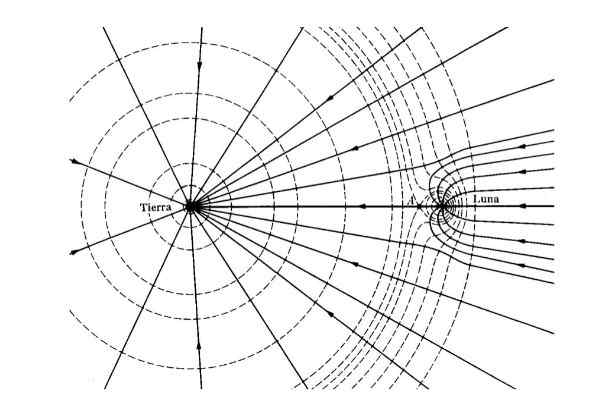figur 2. Gravitationsfält (kontinuerliga linjer) och jämlikhet (segmenterad linje) för jorden - Luna -systemet. Källa: W T Scott, AM. J. Fysik. 33, (1965).

Ansökningar

Gravitational Potential Energy är vad kropparna lagrar när de är i ett gravitationsfält.

Till exempel har vattnet i en tank mer energi i den utsträckning tanken är högre höjd.

Vid en högre tank, desto större är vattenutloppshastigheten vid kranen. Detta beror på att den potentiella energin i vatten på tankens höjd omvandlas till kinetisk vattenenergi vid kranens utgång.

När vattnet skadas på toppen av ett berg kan den potentiella energin användas för att rotera elproduktionsturbinerna.

Gravitationsenergi förklarar också tidvatten. Eftersom energin och gravitationsstyrkan beror på avståndet, är månens gravitationella drag större i ansiktet av landet närmast månen än det längsta och mest motsatta ansiktet.

Detta ger en skillnad i krafter som deformerar havsytan. Effekten är större på en nymåne när solen och månen är inriktade.

Möjligheten att bygga rumsliga och satellitstationer som förblir relativt nära vår planet beror på gravitationsenergi som produceras av jorden. Om inte rymdstationer och konstgjorda satelliter skulle vandra genom rymden.

Det kan tjäna dig: Imantation: Vad består, metod och exempel

Jordens gravitationspotential

Antag att jorden har massa M och ett objekt som är över jordens yta på avstånd r När det gäller mitten av samma har en massa m. 

I detta fall bestäms gravitationspotentialen utifrån gravitationsenergi som helt enkelt delas mellan massans massa som resulterar:

Gravitationspotentialen på jordens yta erhålls genom att ersätta r Av den markbundna radien r_T. 

Potentiell energi nära jordens yta

Anta att jorden har radio R_T  och massa M.

Även om jorden inte är ett snabbt objekt är fältet på dess yta motsvarande det som skulle erhållas om all dess massa M Det koncentrerades i mitten, så att gravitationsenergin hos ett föremål vid höjd h på jordens yta är 

U (r_T + h) = -G.M m (r_T + h)^-1

Men eftersom H är mycket mindre än R_T, Det tidigare uttrycket kan närma sig 

U = uo + mgh

Där g är tyngdkraften, vars genomsnittliga värde för jorden är 9.81 m/s^2.

Då är den potentiella energip -ep för en massa m vid höjden h på jordens yta:

EP (h) = u +uo = mgh

På jordens yta h = 0, så ett objekt på ytan har EP = 0. Detaljerade beräkningar kan ses i figur 3.

Figur 3. Gravitationspotential energi i en höjd h på ytan. Källa: Utarbetad av F. Zapata.

Övningar 

Övning 1: Gravitational Earth Collapse

Antag att vår planet lider av en gravitationskollaps för förlust av termisk energi inuti och dess radie sönderfaller upp till hälften av det nuvarande värdet men planetens massa är konstant.

Bestäm vad som skulle vara tyngdkraften nära ytan på det nya landet och hur mycket en överlevande väger 50 kg-F före kollapsen. Ökar eller minskar personens gravitationsenergi och i vilken faktor.

Lösning

Acceleration av tyngdkraften på ytan på en planet beror på dess massa och dess radie. Gravitationskonstanten är universell och tjänar lika för planeter och exoplaneter.

I det fall vi är uppvuxna, om jordens radie reduceras med hälften, skulle svårighetsgraden av det nya landet vara fyra gånger större. Detaljerna kan ses på nästa bräde.

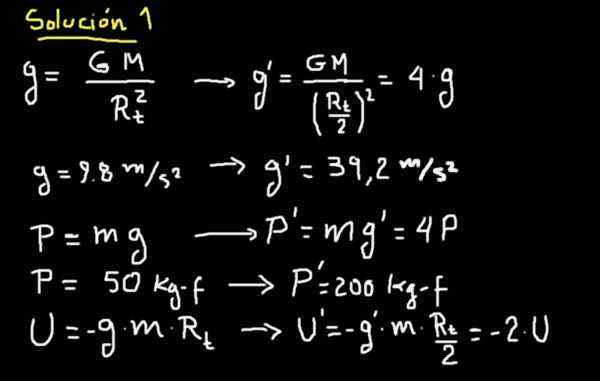
Detta innebär att en superman och överlevande som på den gamla planeten vägde 50 kg-F kommer att väga 200 kg-F på den nya planeten.

Kan tjäna dig: Termisk balans: Ekvationer, applikationer, övningar

Å andra sidan kommer gravitationsenergi att ha reducerats med hälften på ytan på den nya planeten.

Övning 2: Gravitationskollaps och flykthastighet

Med hänvisning till den situation som tas upp i övning 1, vad skulle hända med avgashastigheten: ökar, minskar, i vilken faktor?

Lösning 2

Avgashastigheten är den minsta hastighet som krävs för att undkomma gravitationens attraktion på en planet.

För att beräkna det antas det att en projektil som skjuter med denna hastighet når oändligheten med nollhastighet. Dessutom är i oändlighet gravitationsenergi noll. Därför kommer en projektil som skjuter med avgashastigheten att ha noll total energi.

Det vill säga att på planetens yta vid tidpunkten för skottet måste summan av den kinetiska energin i projektilen + gravitationsenergi upphävas:

½ m ve^2 - (g m.herr_T = 0

Observera att avgashastigheten inte beror på degen för projektilen och dess kvadratvärde är

Ve^2 = (2g m) / r_T

Om planeten kollapsar upp till en radie hälften av originalet blir kvadratet för den nya avgashastigheten dubbel.

Därför växer den nya avgashastigheten och blir 1.41 gånger den gamla flykthastigheten:

Ve '= 1.41 se

Övning 3: Apple Gravitational Energy

En pojke på balkongen i en byggnad 30 meter från marken släpper ett äpple på 250 g, som efter några sekunder når marken.

Figur 4. Under fallet förvandlas äpplets potentiella energi till kinetisk energi. Källa: Pixabay.

a) Vad är gravitationsenergiskillnaden för äpplet högst upp på äpplet på jordnivå?

b) Hur snabbt gjorde äpplet precis innan det sprids på marken?

c) hur är det med energi när äpplet krossade mot marken? 

Lösning

a) Skillnaden i gravitationsenergi är 

m.g.H = 0.250 kg * 9.81 m/s^2 * 30 m = 73.6 j

b) Den potentiella energin som äpplet hade när det var 30 m högt förvandlas till kinetisk energi för när äpplet når marken.

½ m v^2 = m.g.h

V^2 = 2.g.h

Genom att ersätta värden och rensning följer det att äpplet når marken med en hastighet på 24.3 m/s = 87.3 km/h.

c) Naturligtvis är äpplet spridd och all gravitationsenergi som samlas i början går förlorad i form av värme, eftersom äppeldelarna och slagzonen värms upp, dessutom sprids en del av energin också i form av ljudvågor ”Splash".

Referenser

1. Alonso, m. (1970). Volymfysik. 1, Inter -American Education Fund. 
2. Hewitt, Paul. 2012. Konceptuell fysisk vetenskap. Femte. Ed. Pearson.
3. Riddare, r. 2017. Fysik för forskare och teknik: En strategistrategi. Pearson.
4. Sears, f. (2009).University Physics Vol. 1 
5. Wikipedia. Gravitationsenergi. Återhämtad från: är.Wikipedia.com
6. Wikipedia. Gravitationsenergi. Hämtad från: i.Wikipedia.com