Helmholtz Free Energy -enheter, hur det beräknas, lösta övningar

De Helmholtz gratis energi Det är en termodynamisk potential som mäter det användbara arbetet för ett stängt system i konstant temperatur och volymförhållanden. Helmholtzs fria energi betecknas som F Och det definieras som skillnaden från intern energi ELLER Mindre temperaturprodukten T För entropi S:

F = u - t⋅s

Eftersom det är energi mäts det i Joules i det internationella systemet (SI), även om andra lämpliga enheter också kan vara Ergios (CGS), kalorier eller elektronvolt (EV).

Figur 1. Definition av Helmholtzs energi. Källa: Pixabay.

Den negativa variationen i Helmholtzs energi under en process likställs med det maximala arbete som systemet kan utföra i en isokorisk process, det vill säga till konstant volym. När volymen inte är konstant kan en del av detta arbete göras på miljön.

I det här fallet hänvisar vi till arbete där volymen inte varierar, till exempel elektriskt arbete: dw = φdq, med φ som den elektriska potentialen och q som elektrisk laddning.

Om temperaturen också är konstant minimeras Helmholtzs energi när balansen uppnås. För allt detta är Helmholtzs energi särskilt användbar i ständiga volymprocesser. I det här fallet har du:

- För en spontan process: ΔF < 0

- När systemet är i jämvikt: Δf = 0

- I en icke-spontan process: Δf> 0.

[TOC]

Hur beräknas Helmholtz Free Energy?

Som nämnts i början definieras Helmholtzs energi som "den inre energin eller systemet, utom produkten från systemets absolut t -temperatur, av systemets entropi":

F = u - t⋅s

Det är en funktion av temperaturen t och volym v. Stegen för att visualisera detta är följande:

Kan tjäna dig: interna elektroner

- Från och med den första termodynamiklagen, intern energi eller är relaterad till systemets entropi och dess volym V för reversibla processer genom följande differentiella relation:

DU = DQ - DW = TDS - PDV

Detta följer den inre energin eller är en funktion av variabler S och V, därför:

U = u (s, v)

- Nu definitionen av F Och det härleds:

df = du - d (ts) = du - tds - sdt

- Att ersätta där det differentiella uttrycket erhållet för DU i det första steget, kvarstår:

DF = TDS - PDV - TDS - SDT = -SDT - PDV

- Slutligen dras slutsatsen att F är en funktion av temperaturen T och volym V och kan uttryckas som:

F = f (t, v)

figur 2. Hermann von Helmholtz (1821-1894), tysk fysiker och läkare, erkänd för sina bidrag till elektromagnetism och termodynamik, bland andra vetenskapsområden. Källa: Wikimedia Commons.

Spontana processer

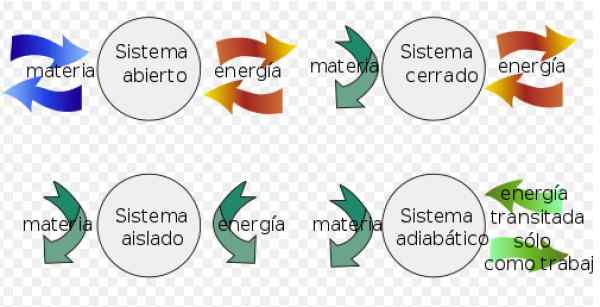
Helmholtzs energi kan tillämpas som ett allmänt kriterium för spontanitet i isolerade system, men innan vissa koncept bör anges:

- En systemets slutna Det kan byta energi med miljön, men kan inte utbyta materia.

- Istället a isolerat system utbyter inte materia eller energi med miljön.

- Äntligen a öppna system utbyte av materia och energi med miljön. 

Figur 3. Termodynamisk system. Källa: Wikimedia Commons. Fjgar (BIS) [CC BY-SA (https: // CreativeCommons.Org/licenser/BY-SA/4.0)].

I reversibla processer beräknas variationen i intern energi enligt följande:

DU = TDS - PDV

Anta nu en konstant volymprocess (isokorisk), där den andra termen i det tidigare uttrycket har ett nollbidrag. Det måste också komma ihåg att enligt Clausius -ojämlikhet: 

ds ≥ dq/t

Sådan ojämlikhet gäller ett isolerat termodynamiskt system.

Så att för en process (reversibel eller inte) där volymen upprätthålls konstant uppfylls:

Kan tjäna dig: fosforsyra (H3PO4)

T ds ≥ du (Vid fast volym)

Med hänsyn till att:

df = du - t ds 

Vi måste i en isokorisk process vid konstant temperatur uppfylls att: Df ≤ 0, Som anges i början.

Så att Helmholtz F: s energi är en minskande mängd i en spontan process medan det är ett isolerat system. F når sitt minsta och stabila värde när reversibel balans har uppnåtts.

Löst övningar

Övning 1

Beräkna variationen i den fria energin från Helmholtz F för 2 mol idealisk gas vid en temperatur av 300K under en isotermisk expansion som leder till systemet med en initial volym på 20 liter till en slutlig volym av 40 liter.

Lösning

Från definitionen av F:

F = u - t s

Då kommer en ändlig variation av F, kallad ΔF, att vara:

ΔF = ΔU - T ΔS

Som uttalandet säger att temperaturen är konstant: Δt = 0. I idealiska gaser beror dock intern energi endast på dess absoluta temperatur, men eftersom det är en isotermisk process, då ΔU = 0 och Δf = - t ΔS. För idealiska gaser skrivs entropivariationen i en isotermisk process så här: 

ΔS = n.R.ln (v₂/V₁)

Tillämpa detta uttryck:

ΔS = 2 mol x 8 314 j/(k mol) x ln (40L/20L) = 11,53 j/k

Slutligen är förändringen i Helmholtzs energi:

ΔF = - T ΔS = - 300K x 11,53 J/K = -3457,70 J.

Övning 2

Inuti en cylinder finns en kolv som delar upp den i två sektioner och på varje sida av kolven finns det n Mullvad med en idealisk monoatomisk gas, som visas i figuren nedan.

Cylinderväggarna är bra värmeledare (diatermiska) och är i kontakt med en T -temperaturbehållare_antingen.

Den initiala volymen för var och en av cylindersektionerna är v_1i och v_2i, medan dess slutliga volymer är v_1f och v_2f Efter en kvasiestatisk förskjutning. Kolven rör sig med en kolv som hermetiskt korsar de två cylindertaporna.

Det kan tjäna dig: Tecnecio (TC): Struktur, egenskaper, användningar, erhållning

Det uppmanas att hitta:

a) Förändringen i den inre energin i gas och det arbete som utförts av systemet och

b) Helmholtzs energivariation.

Lösning till

När kolven rör sig kvasiestatiskt måste den yttre kraften som appliceras på kolven balansera kraften på grund av tryckskillnaden i de två sektionerna i cylindern.

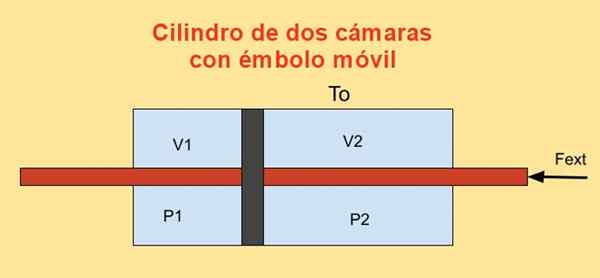Figur 4. Variation av fri energi F i en cylinder med två kameror. Källa: f. Zapata.

Jobbet Dj Gjord av yttre kraft F_ext under en infinitesimal förflyttning Dx är:

Dw = - f_ext Dx = (p₁ - P₂) A dx = p₁ Dv₁ + P₂ Dv₂

Där förhållandet har använts Dv₁ = - DV₂ = En dx, varelse till Kolvområdet. Å andra sidan är variationen i Helmholtzs energi: 

DF = -SDT - PDV

Sedan under processen förändras temperaturen inte, då dt = 0 och Df = - pdv. Tillämpa detta uttryck på varje sektion av cylindern du har:

dw = p₁ Dv₁ + P₂ Dv₂ = - df₁ - Df₂

Varelse F₁  och F₂ Helmholtzs energier i var och en av kamerorna.

Ändligt W -arbete kan beräknas utifrån den ändliga variationen i Helmholtzs energi från varje kamera:

W = -Δf₁ - ΔF₂

Lösning B

För att hitta förändringen av energi från Helmholtz används definitionen: F = u - t s. Som i varje kamera har du en idealisk monoatomisk gas vid konstant temperatur T_antingen, Intern energi förändras inte (ΔU = 0), så att: Δf = - t_antingen ΔS. Förutom:

ΔS = nr ln (v_F/Fick syn på)

Att genom att ersätta det äntligen tillåter det utförda arbete är: 

W = -t_antingen Nr ln (v_1f /V_1i) -To nr ln (v_2f /V_2i) = -Δf₁ -ΔF₂

W = - till nr ln [(v_1f ⋅ v_1i)/(V_{2f .}V_2i)] = - Δf_total

Varelse ΔF_total Den totala variationen i Helmholtzs energi.

Referenser

1. Castaños e. Gratis energiövningar. Återhämtat från: LidiaConlachimica.WordPress.com
2. Librettexts. Helmholtz Energy. Återhämtad från: kem.Librettexts.org
3. Librettexts. Vad är gratis energi. Återhämtad från: kem.Librettexts.org
4. Wikipedia. Helmholtz Energy. Återhämtad från: är.Wikipedia.com
5. Wikipedia. Helmholtz gratis energi. Hämtad från: i.Wikipedia.com