Bas- och dimensionsvektorutrymme, axiomer, egenskaper

En vektorutrymme Det är en icke -tomma uppsättning V= eller, v, W,..., vars element är vektorer. Med dem genomförs några viktiga operationer, bland vilka följande sticker ut:

- Summan mellan två vektorer u + v som ett resultat z, som tillhör helheten V.

- Multiplikation av ett riktigt nummer a av en vektor v: a v som ger en annan vektor och som tillhör V.

Konstnärlig vision av ett vektorutrymme. Källa: Pixabay

För att beteckna en vektor använder vi djärva (v Det är en vektor) och för skalar eller siffror grekiska bokstäver (a är ett nummer).

[TOC]

Axiomer och egenskaper

För att vara ett vektorutrymme måste de nästa åtta axiomerna uppfyllas:

1-konmutbarhet: eller +v = v +eller

2-transitivitet: (eller + v) + W = eller + ( v + W)

3-existens av nollvektorn 0 Så att 0 + v = v

4-existens av det motsatta: motsatsen till v är (-v) , givet att v + (-v) = 0

5-produkter distributivitet med avseende på vektor summan: α ( eller + v ) = αeller +av

6-produkter distributivitet med avseende på skalarsummet: (α + β)v = αv +pv

7-Associativitet för skalprodukten: α (p v) = (α ß)v

8-numret 1 Det är det neutrala elementet sedan: 1v = v

Exempel på vektorutrymmen

Exempel 1

Vektorer i planet (R²) är ett exempel på vektorutrymme. En vektor i planet är ett geometriskt objekt som har storlek och riktning. Det representeras av ett orienterat segment som tillhör nämnda plan och med en storlek proportionell mot dess storlek.

Summan av två vektorer i planet kan definieras som den geometriska driften av den andra vektorn efter den första. Resultatet av summan är det orienterade segmentet som börjar från ursprunget till den första och når spetsen på den andra.

I figuren kan det noteras att summan i R² är kommutativ.

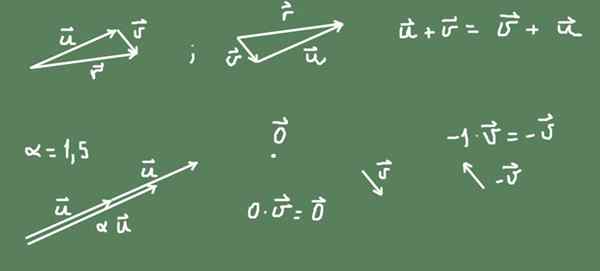figur 2. Vektorer i planet formar vektorutrymme. Källa: Självgjord.

Produkten från ett a -nummer definieras också av en vektor. Om numret är positivt upprätthålls den ursprungliga vektoradressen och storleken är a gånger den ursprungliga vektorn. Om numret är negativt är adressen motsatsen, och den resulterande vektorstorleken är det absoluta värdet på numret.

Vektorn i motsats till en vektor någon v är -v = (-1) v.

Nollvektorn är en punkt i R² -planet, och nollnumret med en vektor resulterar i nollvektorn.

Alla sagt illustreras i figur 2.

Exempel 2

Uppsättning P Av alla polynomer mindre än eller lika med två, inklusive nollklass, bildar de en uppsättning som möter alla axiomerna i ett vektorutrymme.

Det kan tjäna dig: ömsesidigt exklusiva evenemang: egenskaper och exempel

Vara polynomet p (x) = a x² + b x + c y q (x) = d x² + e x + f

Summan av två polynomer definieras: p (x) + q (x) = (a + d) x² + (b + e) ​​x + (c + f)

Summan av polynom som tillhör helheten P Det är kommutativt och transitivt.

Det nollpolynom som tillhör helheten P Det är en som har alla sina koefficienter lika med noll:

0 (x) = 0 x² + 0 x + 0

Summan av en a -skalar definieras av ett polynom såsom: α p (x) = α ∙ a x² + α ∙ B x + α ∙ c

Det motsatta polynomet av p (x) är -p (x) = (-1) p (x).

Från alla ovanstående följer det att uppsättningen P Av alla polynomer mindre än eller lika med två är det ett vektorutrymme.

Exempel 3

Uppsättning M Av alla matriser av M -rader x n -kolumner vars element är verkliga siffror bildar ett verkligt vektorutrymme, med avseende på summan av matriser och produkt av ett nummer av en matris.

Exempel 4

Uppsättningen f för kontinuerliga funktioner för verklig variabel, bildar ett vektorutrymme, eftersom summan av två funktioner kan definieras, multiplikationen av en skalar av en funktion, nollfunktionen och den symmetriska funktionen. De uppfyller också axiomerna som kännetecknar ett vektorutrymme.

Bas och dimension av ett vektorutrymme

Bas

En uppsättning linjärt oberoende vektorer definieras som grunden för ett vektorutrymme så att från en linjär kombination av dem kan varje vektor i det vektorutrymmet genereras.

Linjärt kombinerar två eller flera vektorer består av att multiplicera vektorer av vissa skalar och sedan lägga till dem vektor.

I vektorns vektorutrymme i tre dimensioner bildas till exempel av R³ den kanoniska basen definierad av enhetsvektorerna (av storlek 1) används (av storlek 1) Yo, J, k.

Var Yo = (1, 0, 0); J = (0, 1, 0); k = (0, 0, 1). Dessa är kartesiska eller kanoniska vektorer.

Valfri vektor V tillhör R³ är skriven som V = a Yo + b J + c k, vilket är en linjär kombination av basvektorer Yo, J, k. Skalar eller siffror a, b, c är kända som kartesiska komponenter i V.

Det sägs också att basvektorerna för ett vektorutrymme bildar en uppsättning vektorutrymme.

Dimensionera

Dimensionen av ett vektorutrymme är kardinalnumret för en vektorbas för nämnda utrymme; det vill säga antalet vektorer som utgör nämnda bas.

Denna kardinal är det maximala antalet linjärt oberoende vektorer i det vektorutrymmet, och samtidigt det minsta antalet vektorer som bildar en genererande uppsättning av nämnda rymd.

Kan tjäna dig: statistisk befolkning: koncept, typer, exempel

Baserna i ett vektorutrymme är inte unika, men alla baser i samma vektorutrymme har samma dimension.

Underområde

Ett vektorunderlag av ett vektorutrymme V är en delmängd av V där samma operationer definieras som i V och uppfyller alla axiomerna i vektorutrymmet. Därför kommer underutrymme också att vara ett vektorutrymme.

Exempel på vektor underutrymme är vektorerna som tillhör XY -planet. Detta underutrymme är en delmängd av ett vektorutrymme av dimensionalitet som är större än uppsättningen av vektorer som tillhör det tre dimensionella utrymmet XYZ.

Ett annat exempel på Vector -underområdet S1 i vektorutrymmet bildas av alla 2 × 2 matriser med verkliga element är det som definieras nedan:

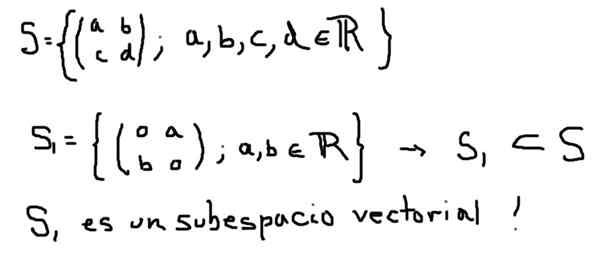
Å andra sidan, S2 som definieras nedan, även om det är en delmängd av S, bildar den inte ett vektoravområde:

Löst övningar

-Övning 1

Vara vektorerna V1= (1, 1, 0); V2= (0, 2, 1) och V3= (0, 0, 3) i R³.

a) bevisa att de är linjärt oberoende.

b) Bevisa att de bildar en bas i R³, eftersom någon lista (x, y, z) kan skrivas som en linjär kombination av V1, V2, V3.

c) Hitta komponenterna i listan V = (-3,5,4) vid basen V1, V2, V3.

Lösning

Kriteriet för att demonstrera linjär oberoende är att fastställa följande uppsättning ekvationer i a, p och y

a (1, 1, 0) + β (0, 2, 1) + γ (0, 0, 3) = (0, 0, 0)

I händelse av att den enda lösningen på detta system är α = β = y = 0 då är vektorerna linjärt oberoende, annars är de inte.

För att uppnå värdena på a, ß och y föreslår vi följande ekvationssystem:

α ∙ 1 + ß ∙ 0 + γ ∙ 0 = 0

α ∙ 1 + β ∙ 2 + γ ∙ 0 = 0

α ∙ 0 + ß ∙ 1 + γ ∙ 3 = 0

Den första leder till α = 0, den andra a = -2 ∙ ß men som α = 0 sedan β = 0. Den tredje ekvationen innebär att γ = (-1/3) ß, men som β = 0 då y = 0.

Svara på

Det dras slutsatsen att det är en uppsättning linjärt oberoende vektorer i R³ .

Svar B

Låt oss nu skriva listan (x, y, z) som en linjär kombination av v1, v2, v3.

(x, y, z) = α V1 + ß V2 + y V3 = α (1, 1, 0) + β (0, 2, 1) + y (0, 0, 3)

α ∙ 1 + β ∙ 0 + γ ∙ 0 = x

α ∙ 1 + ß ∙ 2 + y ∙ 0 = y

Det kan tjäna dig: Tukey Test: Vad är, vid exempel, löste träning

α ∙ 0 + β ∙ 1 + y ∙ 3 = z

Där du har:

α = x

α + 2 β = y

p + 3 y = z

Den första indikerar α = x, den andra β = (y-x)/2 och den tredje y = (z- y/2 +x/2)/3. På detta sätt har vi hittat generatorerna för α, ß och y i någon R³ -lista 

Svar C

Låt oss hitta komponenterna i listan V = (-3,5,4) vid basen V1, V2, V3.

Vi ersätter motsvarande värden i uttryck som finns ovan för generatorerna.

I det här fallet har vi: α = -3; β = (5-(-3))/2 = 4; γ = (4- 5/2 +(- 3)/2)/3 = 0

Det är:

(-3,5,4) = -3 (1, 1, 0) + 4 (0, 2, 1) + 0 (0, 0, 3)

Till sist:

V = -3 V1 + 4 V2 + 0 V3

Vi drar slutsatsen att V1, v2, v3 De bildar en bas i vektorutrymmet R³ i dimension 3.

-Övning 2

Express Polynomial P (T) = T² + 4T -3 som en linjär kombination av P1 (T) = T² -2T + 5, P2 (T) = 2T² -3T och P3 (T) = T + 3.

Lösning

P (t) = x p1 (t) + och p2 (t) + z p3 (t)

där siffrorna x, y, z måste bestämmas.

Genom att multiplicera och gruppera termer med samma examen i t erhålls det:

T² + 4 t -3 = (x + 2y) t² + (-2x -3y + z) t + (5x + 3z)

Vilket leder oss till följande ekvationssystem:

x + 2y = 1

-2x -3y + z = 4

5x + 3z = -3

Lösningarna i detta system med ekvationer är:

x = -3, y = 2, z = 4.

Det är:

P (t) = -3 p1 (t) + 2 p2 (t) + 4 p3 (t)

-Övning 3

Visa att vektorer V1= (1, 0, -1, 2); V2= (1, 1, 0, 1) och V3= (2, 1, -1, 1) av R⁴ är linjärt oberoende.

Lösning

Vi kombinerar linjärt de tre vektorerna V1, V2, V3 Och vi kräver att kombinationen lägger till nollelementet i R⁴

till V1 + b V2 + c V3 = 0

Det vill säga,

A (1, 0, -1, 2) + B (1, 1, 0, 1) + C (2, 1, -1, 1) = (0, 0, 0, 0)

Detta leder oss till följande ekvationssystem:

A + B + 2 C = 0

B + C = 0

-A - C = 0

2 A + B + C = 0

Subtrahera det första och fjärde vi har: -a + c = 0 vad som innebär a = c.

Men om vi tittar på den tredje ekvationen måste vi = -c. Det enda sättet att möta a = c = (-c) är att c är 0 och därför kommer också att vara 0.

A = c = 0

Om vi ​​ersätter detta resultat i den första ekvationen drar vi slutsatsen att b = 0.

Slutligen A = B = C = 0, så det kan dras slutsatsen att vektorer V1, V2 och V3 är linjärt oberoende.

Referenser

1. Lipschutz, s. 1993. Linjär algebra. Andra upplagan. McGraw - Hill. 167 - 198.