Konvex spegel

Vad är en konvex spegel?

han konvex spegel Eller divergerande är en krökt spegel, nästan alltid sfäriskt och med den reflekterande ytan på den yttre sidan av sfären, till exempel jullärens ornament. Tack vare konvexa speglar är det möjligt.

Till exempel är speglarna som placeras på gatorna för att underlätta transitering av fordonen i smala kors konvexa, eftersom de producerar en bild med ett brett synfält.

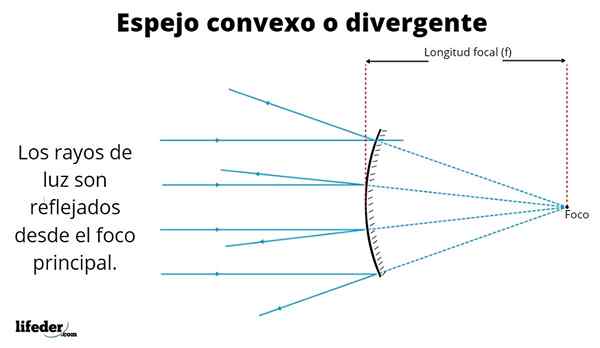
Illustration av en konvex spegel

Bilderna som sålunda bildas är olika, beroende på platsen där objektet placeras. Den överlägsna bilden visar parallella strålar från en avlägsen fontän som solen.

Strålarna återspeglas enligt reflektionslagen, som indikerar att blixidens vinkel är densamma som den återspeglas. Som vi ser är de reflekterade strålarna separerade - de korsar inte - när de lämnar den spekulära ytan, varför denna typ av spegel också kallas avvikande.

När reflektionerna sträcker sig tillbaka från spegeln - diskontinuerliga linjer i figuren - korsar dessa vid en punkt som kallas fokus.

Egenskaper hos konvexa speglar

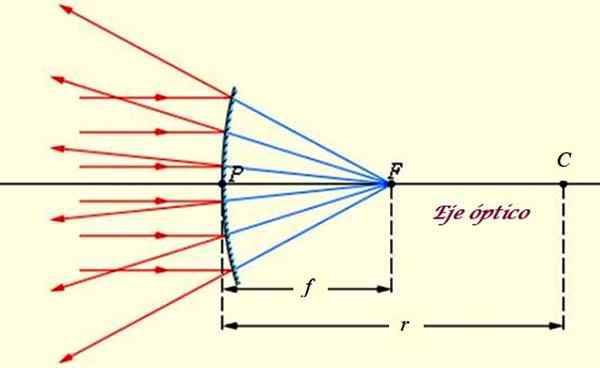Konvex eller divergerande spegel, på vilken strålarna på en avlägsen fontän som solen påverkar. Källa: f. Zapata.

Den konvexa spegeln har följande egenskaper (se överlägsen bild):

-Spegelns anmärkningsvärda punkter är:

• C Centrumet, som sammanfaller med mitten av sfären som spegeln tillhör.
• F Fokus, där strålarna reflekteras bakom spegeln konvergerar.
• Vertex P av samma, som motsvarar mitten av den sfäriska ytan och är kollineal med C och F.

Kan tjäna dig: ío (satellit)

-Har optisk axel antingen huvudaxel, vilket är linjen vinkelrätt mot den spekulära ytan. Strålarna som påverkar den optiska axeln återspeglas i samma riktning.

-Mitten av sfären som spegeln tillhör är vid punkt C och R är dess radie. A C är känd som Krökningscentrum, medan r Är han Krökningsradie och indikerar hur krökt spegel är: en mindre r, Mer accentuerad är den konvexa formen.

-Korsningspunkten för de reflekterade strålarna kallas Brännpunkt av spegeln. Avståndet mellan F och P är ungefär r/2:

F = r/2

Detta uttryck är giltigt för speglar vars storlek är mycket lägre än dess krökningsradie.

-Bilden som bildas är mindre och också virtuell, eftersom den ligger bakom spegeln, som vi kommer att se nästa.

Bildbildning i den konvexa spegeln

Att veta hur bilden som bildas i den konvexa spegeln är strålbehandlingen, som består av att representera de ljusstrålar som kommer ut ur objektet genom raka linjer.

Dessa strålar återspeglas på spegelns yta och de reflekterade strålarna dras också. Ray -metoden är tillämplig på någon form av spegel, inte bara konvexer.

Genom att förlänga de reflekterade strålarna korsar de vid en viss punkt, och det är just där bilden bildas. Förlängningen av de reflekterade strålarna som kommer från ett utökat objekt som ett träd, visas i den nedre figuren av diskontinuerliga linjer.

I den nedre figuren dras tre strålar från objektet, mycket speciellt och enkla att rita, liksom dess reflektioner:

Kan tjäna dig: termisk dilatation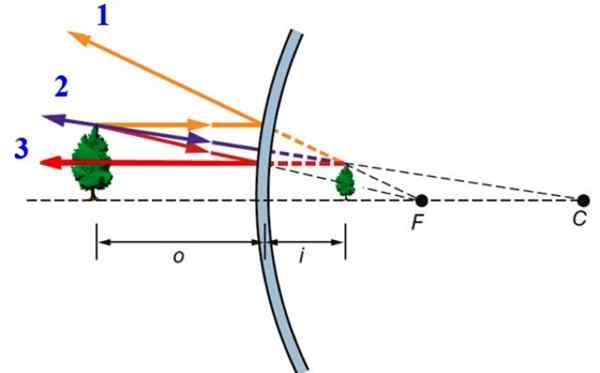 figur 2.- Bildbildning i den konvexa spegeln. Källa: f. Zapata.

-Ray 1, som påverkar parallellt med den optiska axeln.

-Ray 2, som påverkar utlösningen av den reflekterade strålen passerar exakt genom spegelns fokus, det vill säga punkt F. Denna stråle återspeglas parallellt med den optiska axeln.

-Slutligen Ray 3, som når vinkelrätt mot den sfäriska ytan, och av denna anledning återspeglas det i samma riktning.

I princip gäller denna procedur för varje punkt i trädet, men med informationen erhållen från de 3 ritade strålarna räcker det för att hitta bilden av objektet: den bildas bakom spegeln är den rätt och mindre än originalet.

Exempel och tillämpningar av konvexa speglar

Många mycket dragna sfäriska ytor fungerar som konvexa speglar, till exempel ljusa och silver julprydnader, samt nya och ljusa stålskedar.

Även konvexa speglar har till exempel många praktiska tillämpningar: till exempel:

Speglar för att förhindra trafikolyckor

Konvexa speglar på gator och vägar hjälper till att undvika olyckor, eftersom de tillåter dig att se trafiken som kommer från hörnen.

Övervakningsspeglar

I butiker och banker finns det vanligtvis konvexa speglar för att upptäcka tjuvar, liksom att undvika kollisioner mellan människor och gaffeltruckfordon som cirkulerar i hallarna och mellan hyllorna.

Backspeglar

Bilar och motorcyklar har konvexa speglar, som producerar något mindre bilder, men täcker mer synfält än platta speglar.

Cassegrain teleskop

En av speglarna i Cassegrain -reflektorn, den sekundära spegeln, är konvex, även om den inte är sfärisk och tjänar till att återspegla bilden mot teleskopets huvudspegel.

Kan tjäna dig: gravitationsenergi: formler, egenskaper, applikationer, övningar

Konvexa spegelekvationer

Tänk på rektanglarna i följande figur, bestämda av Ray 1, som kommer från toppen av pilen, dess reflektion och förlängningen av detta.

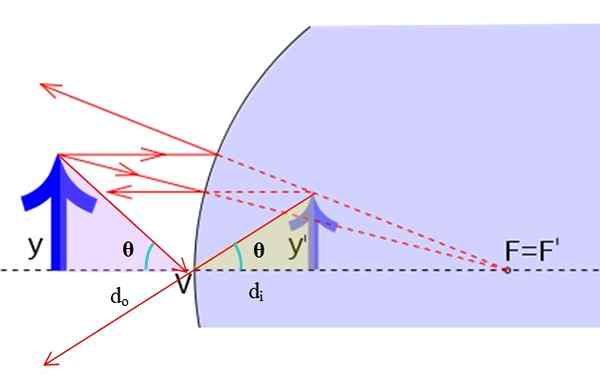Geometri för att hitta spegelförstoringen. Källa: f. Zapata.

Den ursprungliga bilden har höjd och medan höjden på den virtuella bilden är och ' . Är det sant att:

Solbränna θ = y/d_antingen = Y '/d_Yo

Spegelförstoring

Orsaken mellan bildens höjd och objektets höjd är spegelförstoring, Det kallas det, även om den erhållna bilden är mindre än det verkliga objektet. Vi betecknar det med m:

M = y '/ y = D_Yo /d_antingen

Förhållandet mellan objektet och dess bild i den konvexa spegeln

Låt oss nu överväga denna andra figur, där AVF -regionen kan betraktas ungefär som en höger triangel, eftersom spegelns krökning inte är särskilt uttalad. Därför:

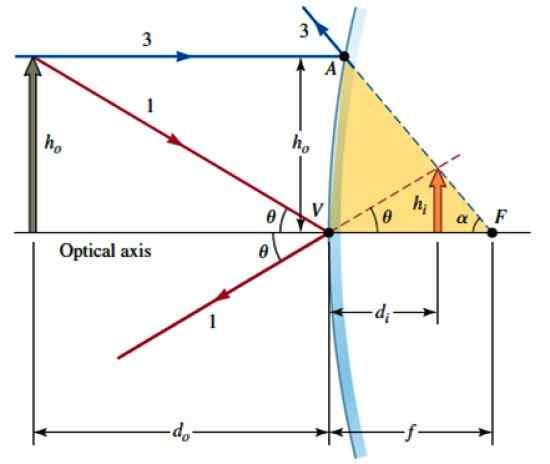Geometri för att hitta det matematiska förhållandet mellan objektet och dess bild. Källa: Katz, D. Fysik för forskare och ingenjörer.

Av ≈ h_antingen

Så:

Solbränna α = h

Därför:

Det omvända av detta uttryck är förstoringen, då:

Därför:

1- (D_Yo /f) = D_Yo /d_antingen

Genom att dela allt mellan D_Yo:

Till sist:

 För speglar gäller vissa teckenkonventioner. Även om vi vet att ett avstånd alltid är positivt, på alla avstånd bakom spegeln, är de utmärkt med ett negativt tecken.

Därför, som F och d_Yo De ligger bakom spegeln, de sätter ett tecken mindre, medan för avståndet d_antingen Det är inte nödvändigt, eftersom det är före spegeln. Således kvarstår den tidigare ekvationen:

Det kan demonstreras att denna ekvation också är giltig för den konkava spegeln.

Referenser

1. Bauer, w. 2011. Fysik för teknik och vetenskap. Volym 2. MC Graw Hill.
2. Giambattista, a. 2010. Fysik. 2: a. Ed. McGraw Hill.
3. Katz, D. 2017. Fysik för forskare och ingenjörer. Cengage Learning.
4. Thomas, w. 2008. Konceptuell fysik. McGraw Hill.
5. Tippens, s. 2011. Fysik: koncept och applikationer. Sjunde upplagan. McGraw Hill.