Funktionsutvärdering

För att utvärdera en funktion som diagrammet är känt, för ett visst värde eller element i startuppsättningen, räcker det att observera motsvarande element i ankomstuppsättningen. Källa: f. Zapata.

Vad är utvärderingen av funktioner?

De Funktionsutvärdering Den består av att bestämma bilden av ett visst domänvärde. Med andra ord, för ett givet värde på startuppsättningen måste du hitta motsvarande i ankomstuppsättningen.

En funktion kan representeras på flera sätt. Om till exempel Venn -diagrammet är tillgängligt är utvärderingen mycket enkel, räcker det att välja elementet i start- eller domänuppsättningen och se elementet som motsvarar ankomstuppsättningen.

I "…… är huvuddiagram ...", representerat ovan, när du utvärderar denna funktion i "Kanada" -elementet, är det "Ottawa" -elementet, i händelse av att göra det med "Mexiko", är det "Mexico City" och så vidare.

Om funktionen ges i form av snygga par är utvärderingen också enkel: den andra medlemmen i det ordnade vridmomentet är bilden av den första medlemmen. Till exempel med funktionen f (x) som beskrivs av:

f (x) = (0,0); (1.2); (2,4); (3,6); (4.8); (5.10); (6,12)

Vid utvärdering av funktionen för värde 3 är resultatet 6; Vid utvärdering av 5 är det 10 och så vidare.

På samma sätt kan en funktion utvärderas när grafen är tillgänglig, förutsatt att det värde du vill utvärdera visas i den.

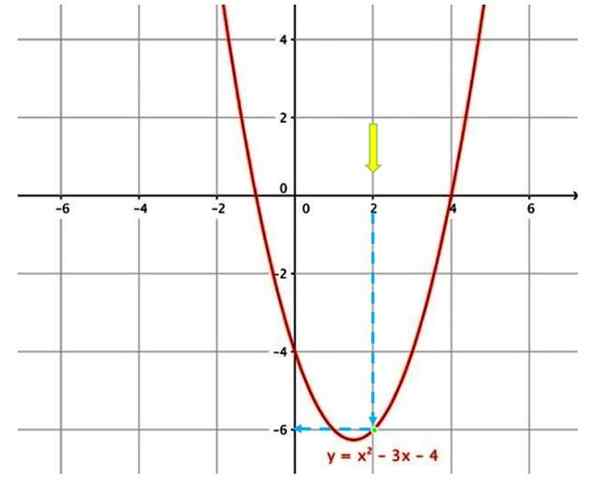Graf för att utvärdera en funktion

För att till exempel utvärdera funktionen som visas ovan, vid x = 2, är det första att hitta i graf a x = 2 (gul pil).

Sedan måste du flytta efter den blå vertikala pilen tills du berör kurvan (grön punkt). Följ den blå pilen igen, vilket indikerar motsvarande värde på den vertikala axeln, därför när du utvärderar funktionen vid x = 2 erhålls y = −6.

Det kan tjäna dig: trigonometriska funktioner: grundläggande, i det kartesiska planet, exempel, träning

Utvärdera en given funktion i matematisk notation

I den nedre delen av grafen ovan visas den grafiska funktionen, men ges i matematisk notation, det vill säga genom en formel:

f (x) = x² - 3x - 4

När du vill utvärdera funktionen i valfritt värde x = a, måste du hitta f (a), som helt enkelt läses "f of a".

För att hitta resultatet ersätts x = a i funktionsformeln, och de begärda operationerna och beräkningarna utförs där.

Anta att du vill utvärdera exemplets funktion vid x = −1. Detta innebär att F (−1) måste hittas.

Det första steget är att ersätta x = -1 i funktionen:

f (−1) = (−1)² - 3 ∙ (−1) - 4

Och sedan utföra de angivna operationerna, som i detta exempel är:

• Hitta kvadratet på −1: (−1)² = 1
• Subtrahera det föregående värdet på produkt 3 ∙ (−1): 3 ∙ (−1) = −3
• Från föregående resultat, subtrahera 4

f (−1) = (−1)² - 3 ∙ (−1) - 4 = 1 + 3 - 4 = 0

Läsaren kan bekräfta detta resultat, från funktionen för funktionen.

Den beskrivna proceduren kan användas för att utvärdera funktionen vid något annat domänvärde. Till exempel kan du hitta f (-2), f (100) eller till och med f (h), där h är ett godtyckligt variabelt värde, som tillhör funktionens domän.

Utvärdera en funktion vid ett värde x = h 

Anta att du vill utvärdera funktionen till något godtyckligt värde, en ofta operation i matematisk beräkning.

I detta fall ersätts X av H, på samma sätt som görs när X tar något numeriskt värde, och resultatet förenklas så mycket som möjligt.

När den resulterande operationen inte längre kan förenklas är den resulterande operationen kvar.

Det kan tjäna dig: ENEGON: Egenskaper, hur man gör en ENEGON, exempel

Exempel

Du vill utvärdera funktionen f (x) = x² - 3x - 4 vid x = h+1. Det nödvändiga tillvägagångssättet är som följer:

f (h+1) = (h+1)² - 3 ∙ (H+1) - 4

Till höger om jämlikhet är den första terminen en anmärkningsvärd produkt:

(H+1)² = h² +2h + 1

Följande termin löses genom distribuerande egendom:

3 ∙ (H + 1) = 3H + 3

När du ersätter allt ovanstående har du:

f (h+1) = (h+1)² - 3 ∙ (H+1) - 4 = H² +2H + 1 - (3H + 3) - 4

De liknande termerna reduceras med algebraisk summa:

f (h+1) = h² + 2H + 1 - 3H - 3 - 4 = H² - H - 6

Differentialkvoten

Differentialkvoten eller förhållandet mellan skillnader D för en funktion f (x) definieras som:

Med tillstånd H ≠ 0, vilket är nödvändigt, eftersom uppdelningen med 0 inte är definierad.

Denna kvot tolkas geometriskt som lutningen för en sekantslinje till kurvan, det vill säga en linje som passerar genom två punkter av den. Koordinaterna för dessa punkter är: [x, f (x)] och [x+h; f (x+h)], som framgår av följande figur:

Differentialkvoten motsvarar att beräkna lutningen på Secant -linjen till kurvan, som passerar genom de angivna punkterna. Källa: Wikimedia Commons.

Det är därför denna kvoter visas i beräkningen av derivatet av en funktion, eftersom det gör att "H" tillvägagångssättet är värdet 0, tenderar att bli en tangentlinje vid punkten (x, y), eftersom punkterna i skärningspunkten av Figuren är så nära att de tenderar till samma punkt.

Således blir linjen tangent (avlyssnar kurvan i en enda punkt).

Detta är just definitionen av härrörande från en funktion: lutningen på linjen tangent till kurvan i koordinatpunkt (x, f (x))).

Det kan tjäna dig: Vägt media: Hur det beräknas, exempel och övningar

Som framgår kräver differentiekvoten utvärdering av funktionen i (x + h) och i x. Följande exempel illustrerar hur man gör det.

Exempel 1

Du vill hitta differentiekvoten för funktionen f (x) = 2x - 3. Det första steget är att höja utvärderingen av funktionen för x = x + h, så här:

f (x+h) = 2 ∙ (x+h) - 3 = 2x+2h - 3

Sedan ersätts resultatet i definitionen av D, givet tidigare:

Med h ≠ 0.

Siffran förenklas så långt som möjligt, vilket minskar liknande villkor:

Slutligen förenklas de vanliga faktorerna i teller och nämnaren:

D = 2

Exempel 2

Hitta differentiekvoten för funktionen f (x) = x² - 3x - 4.

Vi fortsätter som i föregående exempel och hittar första f (x+h), ersätter resultatet i d och förenklar maximalt:

f (x+h) = (x+h)² - 3 (x+h) - 4 = x² + 2hx + h² - 3x - 3h - 4

= 2x+h-3

Därför:

D = 2x+H-3

Där h ≠ 0.

Löst övningar

Övning 1

Utvärdera funktionen f (x) = 2x² - 4x + 1 när:

a) x = -1
b) x = 0
c) x = 2

Lösning till

F (-1) = 2 (-1)² - 4 (-1) + 1 = 2 + 4 + 1 = 7

Lösning B

f (0) = 2 (0)² - 4 (0) + 1 = 0 - 0 + 1 = 1

Lösning C

f (2) = 2 ∙ 2² - 4 ∙ 2 + 1 = 8 - 8 + 1 = 1

Övning 2

Ett naturvårdsteam bestämde att funktionen w (t) = 0.lt² + 1.8t tjänar till att modellera mängden avfall "W", i kilogram, som kastas in i en viss flod, i en tid "T", som ges i dagar.

Beräkna mängden avfall som kastas i floden i slutet av:

a) 3 dagar
b) 1 vecka
c) 1 månad

Lösning till

W (t) -funktionen utvärderas vid t = 3 dagar:

W (3) = 0.1 × 3² +1.8 × 3 = 0.9 + 5.4 = 6.3 kg

Lösning B

Innan du utvärderar måste du spendera en vecka till dagar:

1 vecka = 7 dagar

W (7) = 0.1 × 7² +1.8 × 7 = 4.9 + 12.6 = 17.5 kg

Lösning C

Återigen är det nödvändigt att omvandla månaderna till dagar:

1 månad = 30 dagar

W (30) = 0.1 × 30² +1.8 × 30 = 90 + 54 = 144 kilo

Referenser

1. Larson, r. 2012. Förkalkning. 8th. Utgåva. Cengage Learning.
2. Monterey Institute. Utvärdering av funktioner. Återhämtat sig från: MontereyInstitute.org.
3. Stewart, J. 2007. Preccculment: Matematik för beräkning. Femte. Utgåva. Cengage Learning.
4. Sullivan, m. 1997. Förkalkning. 4th. Utgåva. Pearson Education.
5. Zill, D. 2008. Preccculment med beräkningsförskott. 4th. Utgåva. McGraw Hill.