Millikan experimentförfarande, förklaring, betydelse

han Millikan experiment, Utförs av Robert Millikan (1868-1953) med sin student Harvey Fletcher (1884-1981), började 1906 och syftade till att studera egenskaperna för den elektriska laddningen och analysera rörelsen av tusentals oljedroppar mitt i en enhetlig elektrisk elektrisk fält.

Slutsatsen var att den elektriska laddningen inte hade ett godtyckligt värde, men att den kom i multiplar av 1.6 x 10^-19 C, som är den grundläggande belastningen på elektronen. Dessutom hittades elektronmassan.

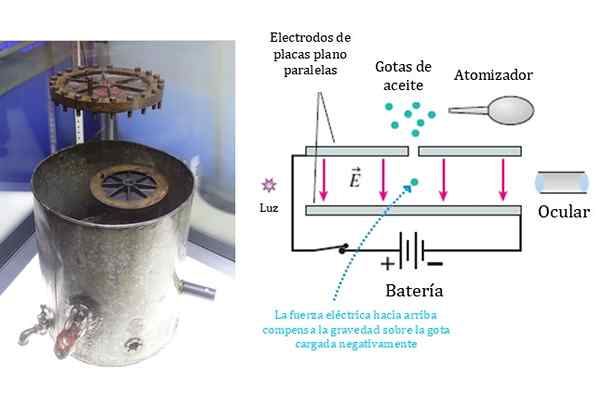
Figur 1. Till vänster den ursprungliga enheten som används av Millikan och Fletcher i sitt experiment. Till höger ett förenklat schema av samma. Källa: Wikimedia Commons/F. Zapata,

Tidigare den fysiska J.J. Thompson hade funnit experimentellt belastnings-mandyförhållandet mellan denna elementära partikel, som han kallade "corpuscle", men inte värdena för varje storlek separat.

Från denna belastning - massförhållande och elektronbelastningen bestämdes värdet på dess massa: 9.11 x 10^-31 Kg.

För att uppnå sitt syfte serverade Millikan och Fletcher en finfördelare med vilken en fin dimma med oljedroppar sprayades. Några av dropparna laddades elektriskt tack vare friktion i sprutan.

Lastade droppar satte sig långsamt på parallella platta plackelektroder, där några få passerade genom ett litet hål i den övre plattan, som visas i schemat i figur 1.

Inuti parallella plattor är det möjligt att skapa ett enhetligt elektriskt fält och vinkelrätt mot plattorna, vars storlek och polaritet kontrollerades genom att modifiera spänningen.

Dropparnas beteende observerades genom att belysa plattans insida med ett starkt ljus.

[TOC]

Experimentets förklaring

Om droppen har en belastning utövar fältet som skapas mellan plattorna en kraft på den som motverkar tyngdkraften.

Och om det också lyckas bli avstängd, betyder det att fältet utövar en vertikal kraft upp, som exakt balanserar till allvar. Detta tillstånd beror på värdet av q, giktbelastningen.

Millikan observerade faktiskt att efter att ha slagit på fältet, vissa droppar avbröts, andra började klättra eller fortsatte att gå ner.

Justera värdet på det elektriska fältet -genom variabel motstånd, till exempel -a droppe kan tillåtas förbli upphängd i plattorna. Även om det i praktiken inte är lätt att uppnå, om det hände, bara den kraft som utövas av fältet och tyngdkraften verkar på fallet.

Kan tjäna dig: absorbans: vad är, exempel och övningar löst

Om massan på droppen är m Och dess last är q, Att veta att kraften är proportionell mot det tillämpade storleksfältet OCH, Newtons andra lag konstaterar att båda styrkorna måste vara balanserade:

mg = q.OCH

Q = mg/e

Värdet av g, Acceleration av tyngdkraften är känd, liksom storleken OCH i fältet, som beror på spänningen V etablerad mellan plattorna och separationen mellan dessa L, som:

E = v/l

Frågan var att hitta massan av den lilla droppen olja. När detta har uppnåtts, bestäm lasten q Det är helt möjligt. Naturligtvis det m och q De är respektive massan och belastningen på droppen olja, inte elektronen.

Men ... droppen laddas eftersom den förlorar eller får elektroner, så dess värde är relaterat till belastningen av nämnda partikel.

Oljefallets massa

Millikan och Fletchers problem var att bestämma massan av en droppe, en uppgift som inte är lätt på grund av den lilla storleken på den.

Att känna till oljans densitet, om du har volymvolymen, kan degen rensas. Men volymen var också mycket liten, så de konventionella metoderna var inte användbara.

Forskare visste emellertid att sådana små föremål inte faller fritt, eftersom luftens eller miljöns motstånd ingår genom att bromsa deras rörelse. Även om partikeln när den släpps med off -fältet upplever en accelererad vertikal rörelse och ner, hamnar den med konstant hastighet.

I denna hastighet kallas det "terminalhastighet" eller "begränsningshastighet", som i fallet med en sfär beror på dess radie och luftviskositet.

I frånvaro av fält mätte Millikan och Fletcher tiden dropparna tog sig för att falla. Antagande att dropparna var sfäriska och med värdet på viskositeten i luften var de fixerade för att bestämma radien indirekt från terminalhastigheten.

Denna hastighet tillämpar Stokes lag och här är dess ekvation:

 Var:

-v_t är terminalhastigheten

-R Det är giktens radie (sfärisk)

-η Det är luftens viskositet

-ρ Det är tätheten på gikt

Betydelse

Millikans experiment var avgörande, eftersom det visade flera viktiga aspekter inom fysik:

I) elementärlasten är den för elektronen, vars värde är 1.6 x 10 ^-19 C, en av vetenskapens grundläggande konstanter.

Ii) någon annan elektrisk laddning kommer i multiplar av den grundläggande belastningen.

Kan tjäna dig: Parabolic Shot: Egenskaper, formler och ekvationer, exempel

Iii) Att känna till elektronens laddning och belastningsförhållandet mellan J.J. Thomson, det var möjligt att bestämma elektronmassan.

Iii) Vid partiklar så små som elementära partiklar är gravitationseffekter försumbara mot elektrostatisk.

figur 2. Millikan i förgrunden till höger, bredvid Albert Einstein och andra anmärkningsvärda fysiker. Källa: Wikimedia Commons.

Millikan fick Nobelpriset i fysik 1923 för dessa upptäckter. Hans experiment är också relevant eftersom han bestämde dessa grundläggande egenskaper för den elektriska laddningen, baserat på enkel instrumentering och tillämpning av lagar som är välkända för alla.

Millikan kritiserades emellertid för att ha uteslutit många observationer i sitt experiment, utan uppenbar anledning, för att minska det statistiska felet i resultaten och att de var mer "presentabla".

Droppar med olika belastningar

Millikan mätte många droppar i sitt experiment och inte alla var olja. Han testade också med kvicksilver och glycerin. Som nämnts började experimentet 1906 och förlängdes under några år. Tre år senare, 1909, publicerades de första resultaten.

Under denna tid erhöll han en mängd laster laddade genom att påverka x -strålar genom plattorna, för att jonisera luften mellan dem. På detta sätt släpps laddade partiklar som droppar kan acceptera.

Dessutom koncentrerades det inte enbart på upphängda droppar. Millikan observerade att när dropparna uppgick varierade också hastigheten på stigningen beroende på den levererade belastningen.

Och om droppen härstammade, var denna extra extra belastning tack vare interventionen av X -Rays, hastigheten varierade inte, eftersom någon massa elektroner som läggs till i droppen är små bokstäver, jämfört med själva droppen.

Oavsett hur mycket belastning han tilllade, fann Millikan att alla droppar förvärvade hela multiplar av ett visst värde, vilket är och, Den grundläggande enheten, som vi har sagt är elektronbelastningen.

Millikan erhöll initialt 1.592 x 10^-19 C för detta värde, något lägre än den som för närvarande accepteras, vilket är 1.602 x 10^-19 C. Anledningen kan ha varit det värde som det gav till luftens viskositet i ekvationen för att bestämma droppens terminalhastighet.

Exempel

Levitera en droppe olja

Vi ser följande exempel. En droppe olja har densitet ρ = 927 kg/m³ och släpps mitt i elektroderna med det elektriska fältet. Droppen når snabbt terminalhastigheten, varvid radien bestäms, vars värde visar sig vara r = 4,37 x10^-7 m.

Kan tjäna dig: Fördelar och nackdelar med friktion

Det enhetliga fältet är påslagen, riktas vertikalt upp och har 9,66 kN/c -storlek . På detta sätt uppnås att droppen är avstängd i vila.

Det begärs:

a) Beräkna droppbelastningen

b) Hitta hur många gånger den elementära belastningen som finns i droppbelastningen.

c) Bestäm om möjligt, tecknet på lasten.

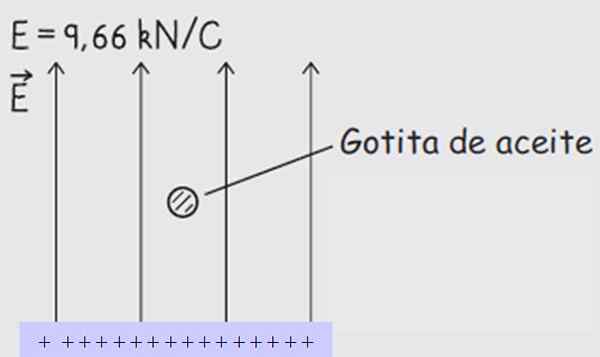Figur 3. En droppe olja mitt i ett konstant elektriskt fält. Källa: Fundamentals of Physics. Rex-Wolfson.

Lösning till

Tidigare härleddes följande uttryck för en vilande droppe:

Q = mg/e

Genom att känna till tätheten och radien för gikt bestäms massan av detta:

ρ = m /v

V = (4/3) πr³

Därför:

m = ρ.V = ρ. (4/3) πr³= 927 kg/m³. (4/3) π.(4,37 x10^-7 m)³= 3.24 x 10^-16 kg

Därför är fallets belastning:

Q = mg/e = 3.24 x 10^-16 kg x 9.8 m/s²/9660 n = 3.3 x 10^-19 C

Lösning B

Att veta att den grundläggande bördan är E = 1.6 x 10 ^-19 C, belastningen som erhållits i föregående avsnitt delas med detta värde:

n = q/e = 3.3 x 10^-19 C1.6 x 10 ^-19 C = 2.05

Resultatet är att laddningsbelastningen är ungefär dubbel (N≈2) av elementärlasten. Det är inte exakt dubbelt, men denna lilla avvikelse beror på den oundvikliga närvaron av det experimentella felet, liksom avrundningen i var och en av de tidigare beräkningarna.

Lösning C

Ja, det är möjligt att bestämma tecknet på lasten, tack vare det faktum att uttalandet ger information om fältets riktning, som riktas vertikalt uppåt, precis som kraften.

De elektriska fältlinjerna börjar alltid från positiva belastningar och slutar i negativa belastningar, därför laddas den nedre plattan med skylt + och den ovan med ett tecken - (se figur 3).

Eftersom droppen riktas mot ovanstående platta som drivs av fältet, och eftersom det motsatta skyltbelastningen lockas, måste droppen ha en positiv laddning.

Egentligen är det inte lätt att hålla den upphängda droppen. Så Millikan använde de vertikala förskjutningarna (UPS.

Denna förvärvade belastning är proportionell mot elektronbelastningen, som vi redan har sett, och kan beräknas med stigningen och nedstigningstider, massan av droppen och värdena på g och OCH.

Referenser

1. Öppet sinne. Millikan, fysikern som kom för att se elektronen. Återhämtat sig från: bbvaopenmind.com
2. Rex, a. 2011. Fysikens grunder. Pearson.
3. Tippens, s. 2011. Fysik: koncept och applikationer. Sjunde upplagan. McGraw Hill.
4. Amrit.  Millikans oljedroppsexperiment. Återhämtat sig från: Vlab.Amrit.Edu
5. Wake Forest College. Millikans oljedroppsexperiment. Återhämtat sig från: WFU.Edu