Elastisk kraft som består, formler och övningar

De elastisk kraft Det är kraften som ett objekt utövar för att motstå en förändring i sin form. Det manifesterar sig i ett objekt som tenderar att återställa sin form när den är under en deformationskraft.

Elastisk kraft kallas också återställande kraft eftersom den motsätter sig deformation för att återlämna objekt till dess jämviktsposition. Överföringen av den elastiska kraften är genom partiklarna som integrerar föremålen.

Vårens elastiska styrka

Till exempel, när en metallfjäder komprimeras utförs en kraft som driver fjäderpartiklarna genom att minska separationen mellan dem, samtidigt motstår partiklarna som utövar en kraft som strider mot komprimering.

Om den i stället för att komprimera våren kastas det, de partiklar som integrerar det är separerade mer. På samma sätt motstår partiklarna att separera en kraft som strider mot sträckning.

Objekt som har egenskapen att återställa sin ursprungliga form genom att motsätta sig deformationskraften kallas elastiska föremål. Fjädrarna, elastiska gummi och elastiska strängar är exempel på elastiska föremål.

[TOC]

Vad är den elastiska kraften?

Den elastiska kraften (F_k) Det är kraften som ett föremål utövar att återvinna sitt naturliga jämvikt genom att ha påverkats av en yttre kraft.

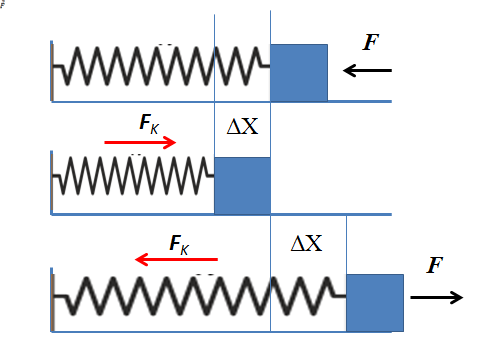
För att analysera den elastiska kraften kommer det ideala fjädermassasystemet att beaktas som består av en horisontellt placerad fjäder som är utsatt för ena änden på väggen och i andra änden till ett block av föraktlig massa. De andra krafterna som verkar på systemet som friktion eller tyngdkraft kommer inte att beaktas.

Det kan tjäna dig: Andra jämviktstillstånd: Förklaring, exempel, övningar

Om en horisontell kraft utövas på degen, riktad mot väggen, överförs den till våren som komprimerar den. Våren rör sig från sin jämviktsposition mot en ny position. När objektet tenderar att förbli i balans manifesteras den elastiska kraften på våren som motsätter sig den applicerade kraften.

Förskjutningen indikerar hur mycket våren och den elastiska kraften har deformerats är proportionell mot den förskjutningen. När våren komprimeras ökar variationen i läget och ökar följaktligen den elastiska kraften.

Ju mer våren komprimeras, desto mer oppositionskraft utövar tills den når en punkt där den applicerade kraften och den elastiska kraften är balanserad, följaktligen slutar vårmassasystemet att röra sig. Genom att sluta tillämpa styrka är den enda kraften den elastiska kraften. Denna kraft påskyndar våren i den riktning som strider mot deformationen tills det återhämtar sig jämviktstillståndet.

På samma sätt som det inträffar när du sträcker våren och tittar på degen horisontellt. Våren är sträckt och utövar omedelbart en kraft som är proportionell mot förskjutning som motsätter sig stretching.

Formler

Den elastiska kraftformeln uttrycks av Hookes lag. Denna lag konstaterar att den linjära elastiska kraften som utövas av ett objekt är proportionellt mot förskjutning.

F_k = -k.Δs         [1]

F_k = Elastisk kraft

k = Proportionalitetskonstant

Δs = Förskjutning

När objektet rör sig horisontellt, som i fallet med fjädern med väggen, är förskjutningen Δx, Och uttrycket av Hookes lag är skriven:

F_k = -k.Δx        [2]

Kan tjäna dig: konvergent lins: egenskaper, typer och träning löst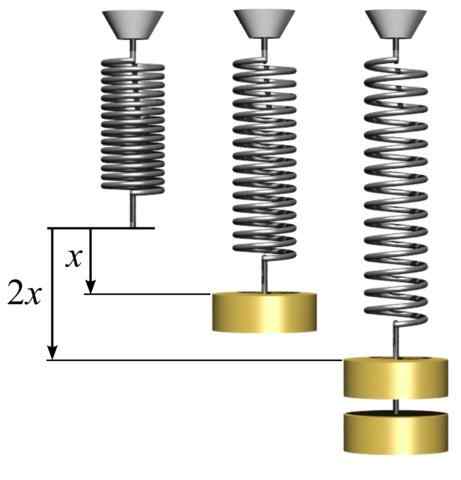Hookes lag. Elastisk kraft proportionell mot sträckning. [Av SVJO (https: // commons.Wikimedia.org/wiki/fil: hookes-slaw-fjädrar.Png)]

Den negativa tecknet i ekvationen indikerar att vårens elastiska kraft är i motsatt riktning mot kraften som orsakade förskjutningen. Proportionalitetskonstanten k Det är en konstant som beror på vilken typ av material som fjädern är utgör. Konstantens enhet k är N/m.

Elastiska föremål har en gräns för elasticitet som beror på deformationskonstanten. Om den sträcker sig bortom den elastiska gränsen kommer den att deformeras permanent.

Ekvation [1] och [2] gäller för små vårförskjutningar. När förskjutningarna är större läggs termer med större kraft av Δx.

Kinetisk energi och potentiell energi hänvisas till en elastisk kraft

Den elastiska kraften fungerar på våren genom att flytta den mot dess jämviktsposition. Under den processen ökar den potentiella energin i vårmassasystemet. Den potentiella energin på grund av det arbete som gjorts av den elastiska kraften uttrycks i ekvation [3].

U = ½ k .  Δx²[3]

Potentiell energi uttrycks i Joules (J).

Genom att sluta tillämpa deformationskraften accelererar våren till jämviktspositionen genom att minska potentiell energi och öka kinetisk energi.

Vårmassasystemets kinetiska energi, när jämviktspositionen når, bestäms av ekvation [4].

OCH_k= ½ m.v²[4]

m = massa

v = fjäderhastighet

För att lösa vårmassasystemet tillämpas Newtons andra lag med hänsyn till att elastisk kraft är en variabel kraft.

Praktiska övningar av exempel

Erhålla deformationskraft

Hur mycket kraft som krävs för att applicera på en fjäder för att sträcka sig 5 cm om fjäderkonstanten är 35N/m?

Kan tjäna dig: Acceleration of Gravity: Vad är det, hur det mäts och övningar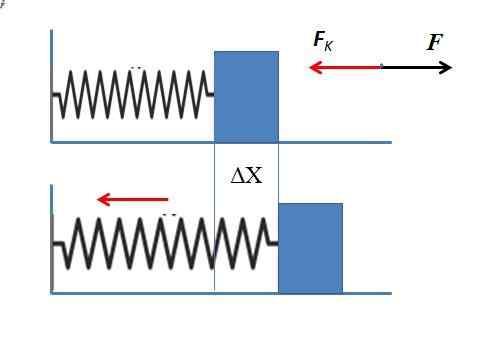Elastisk kraft på en vår som sträcker sig 5 cm

Eftersom tillämpningskraften motsätter sig den elastiska kraften bestäms F_k förutsatt att fjädern är sträckt horisontellt. Resultatet kräver inte det negativa tecknet eftersom applikationskraften endast behövs.

Hookes lag

F_k = -k.Δx       

Konstanten k av våren är 35n/m.

Δx = 5 cm = 0,05 m

F_k = -35n/m . 0,05 m

F_k = - 1,75N = - F

Nödvändig 1,75 n av kraft för att deformera våren 5 cm.

Erhålla deformationskonstanten

Vad är deformationskonstanten för en fjäder som sträcker sig 20 cm genom handlingen av en kraft av 60n?

Δx =20 cm = 0,2 m

F = 60n

F_k = -60n = - f

K = - f_k / Δx

  = -(-60N) /0.2m

K = 300 N/m

Vårkonstanten är 300n/m

Få potentiell energi

Vad är den potentiella energin som hänvisas till det arbete som gjorts av den elastiska kraften på en vår som komprimeras 10 cm Och dess deformationskonstant är 20n/m?

Δx =10 cm = 0,1 m

K = 20 n/m

F_k = -20n/m . 0,1 m

F_k = -200N

Vårens elastiska kraft är -200n.

Denna kraft fungerar på våren för att flytta den mot dess jämviktsposition. När man utför detta arbete ökar systemets potentiella energi.

Potentiell energi beräknas med ekvation [3]

U = ½ k .  Δx²

U = ½ (20n/m) . (0,1 m)²

U = 0,1 joules

Referenser

1. Kittel, C, Knight, W D och Ruderman, M A. Mekanik. USA: MC Graw Hill, 1973, Vol. Yo.
2. Rama Reddy, K, Badami, S B och Balasubramanian, V. Oscillament och vågor. Indien: University Press, 1994.
3. Murphy, J. Fysik: Understanging Egenskaperna för materia och energi. New York: Britannica Education Publishing, 2015.
4. Giordano, n j. College Physics: Resonemang och relationer. Kanada: Brooks/Cole, 2009.
5. Walker, J, Halliday, D och Resnick, R. Fysikens grunder. USA: Wiley, 2014.