Resulterande kraft hur beräknade och lösta övningar

De tvinga resulterande Det är summan av alla krafter som verkar på samma kropp. När en kropp eller objekt är föremål för verkan av flera krafter samtidigt inträffar en effekt. Krafterna som verkar kan ersättas av en enda kraft som ger samma effekt. Denna unika kraft är den resulterande kraften, även känd som nettokraft och representeras med symbolen F_R .

Effekten den producerar F_R Det beror på dess storlek, riktning och mening. De fysiska storleken som har riktning och betydelse är vektorstorlekar.

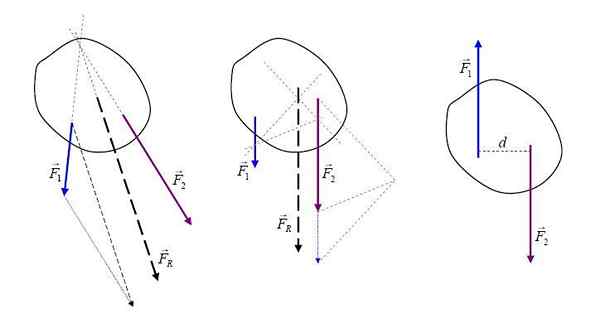Resulterande krafter. Av Ilevanat (https: // commons.Wikimedia.org/wiki/fil: Rejultanta.JPG), från Wikimedia Commons

Att vara de krafter som verkar på en kropps- och vektorstorlekar, den resulterande kraften F_R  Det är en vektor summa av alla krafter och kan representeras grafiskt med en pil som indikerar dess riktning och betydelse.

Med den resulterande kraften förenklas problemet med en kropp som påverkas av flera krafter genom att minska den till en enda styrka som agerar.

[TOC]

Formel

Den matematiska representationen av den resulterande kraften är en sommarvektor av krafterna.

 F_R= ∑F          (1)

 ∑F = f₁+ F₂+ F₃+.. F_N           (2)

F_R= Resulterande kraft

∑F = Styrkor

N= Antal krafter

Den resulterande kraften kan också representeras med ekvationen i Newtons andra lag.

   F_R= m.till          (3)

m= kroppsmassa

A = kroppsacceleration

Om ekvation (1) ersätts i ekvation (3) erhålls följande ekvationer:

∑F = m.till          (4)

F₁+ F₂+ F₃+.. F_{N =} m.till          (5)

Matematiska uttryck (4) och (5) ger information om kroppsstatus genom att få vektoraccelerationen till.

Hur beräknas den resulterande kraften?

Den resulterande kraften erhålls vid tillämpning av Newtons andra lag som fastställer följande:

Kan tjäna dig: distanskrafter

Nettokraften som verkar på en kropp är lika med produkten från dess massa genom den acceleration som den förvärvar. (Ekvation (3))

Kroppens acceleration kommer att ha riktningen för den applicerade nettokraften. Om alla krafter som verkar i kroppen är kända, skulle det räcka för att lägga till det för att få den resulterande kraften. På samma sätt, om den resulterande kraften är känd, skulle den sedan dela upp den med kroppens kropp för att få sin acceleration.

Om den resulterande kraften är ogiltig är kroppen i vila eller konstant hastighet. Om den resulterande kraften verkar på kroppen är en enda kraft lika med den kraften F_R=F.

När flera krafter verkar på samma kropp måste vektorkomponenterna i styrkan beaktas, och om dessa krafter är parallella eller inte.

Om vi ​​till exempel horisontellt skjuter en bok placerad på ett bord. Krafterna i horisontell riktning är de enda som ger acceleration till kroppen. Den vertikala nettokraften på boken är noll.

Om den tillämpade kraften på boken har en lutning med avseende på bordets horisontella plan, skrivs kraften baserat på de vertikala och horisontella komponenterna.

Resulterande av parallella krafter 

De parallella krafterna som verkar på en kropp är de krafter som verkar i samma riktning. De kan vara av två typer av lika känsla eller i motsatt riktning.

När krafterna som verkar på en kropp har samma riktning och samma känsla eller är i motsatt riktning erhålls den resulterande kraften genom att utföra den algebraiska summan av de numeriska värdena för krafterna.

Kan tjäna dig: elektriskt fältflöde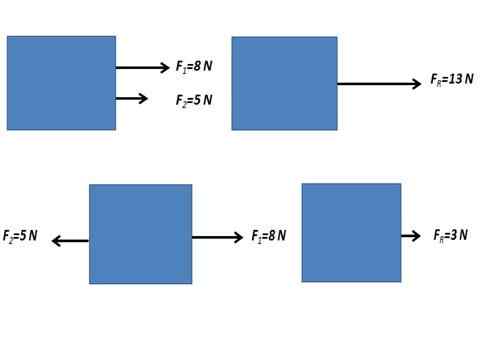Kraft till följd av två parallella krafter.

Icke -parallella krafter

När icke -parallella krafter appliceras på en kropp kommer de resulterande krafterna att ha rektangulära och vertikala komponenter. Det matematiska uttrycket för att beräkna nettokraften är:

F_R²= (∑ f_x)²+(∑ f_och)²            (6)

så θ_x= ∑ f_och / ∑ f_x         (7)

∑ f_x  och ∑ f_x= Algebraisk summa av komponenterna x och och av tillämpade styrkor

θ_x= vinkel som bildar den resulterande kraften F_R Med axeln x

Observera att kraften som härrör från uttrycket (6) inte markeras i djärv bokstav och det beror på att den bara uttrycker det numeriska värdet. Adressen bestäms av vinkeln θ_x.

Uttrycket (6) är giltigt för krafter som agerar i samma plan. När krafterna verkar i rymden beaktas komponenten z av kraft om du arbetar med rektangulära komponenter.

Löst övningar

1. Bestäm de krafter som härrör från en kropp som är föremål för följande krafter som visas i bilden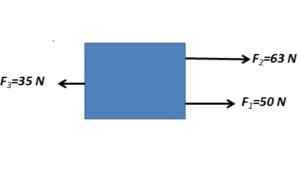

De parallella krafterna läggs till i samma mening och subtraherar med den parallella kraften i motsatt riktning

F_R= 63 n + 50 n - 35 n = 78n

Den resulterande kraften har en storlek på 78n med horisontell riktning.

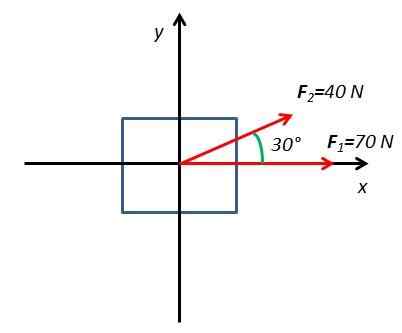
2.Beräkna kraften till följd av en kropp under påverkan av två krafter F_{1 och} F₂. Kraften F₁ Den har en storlek på 70N och appliceras horisontellt. Kraften F₂ Den har en storlek på 40N och appliceras i en vinkel på 30 ° med avseende på det horisontella planet.

För att lösa denna övning dras ett gratis kroppsdiagram med koordinataxlar x och och

Alla komponenter bestäms x och och av krafterna som verkar på kroppen. Kraften F₁ Den har bara en horisontell komponent på axeln x. Kraften F₂ Den har två komponenter F_2x  och f_{2 och} som erhålls från sinus- och kosinusfunktionerna i vinkeln 30.

Kan tjäna dig: friktion: typer, koefficient, beräkning, övningar

F_1x = F₁=70N

F_2x = F₂ Cos 30 ° = 40 n.Cos 30 ° = 34,64N

F_1y = 0

F_{2 och}= F₂ utan 30 ° = 40 utan 30 ° = 20N

∑ f_x =70n+34,64N = 104,64N

∑ f_och=20n+0 = 20n

När de resulterande krafterna på axeln har bestämts x och och Det numeriska värdet på den resulterande kraften erhålls.

F_R²= (∑ f_x)²+(∑ f_och)²

Den resulterande kraften är kvadratroten till sommarsumman av komponenterna i krafterna

F_R= √ (104.64N)²+(20n)²

F_R= 106,53n

Vinkeln som bildar den resulterande kraften F_R Det erhålls från följande uttryck:

θ_x= solbränna^-1(∑ f_och / ∑ f_x)

θ_x= så^-1(20n / 104,64N) = 10,82 °

Den resulterande kraften F_R Den har en storlek på 106,53N och har en riktning bestämd av vinkeln på 10,82 ° som bildas med horisontellt.

Referenser

1. Dola, G, Duffy, M och Percival, till. Fysik. Spanien: Heinemann, 2003.
2. Avisison, J H. Fysikens värld. Indien: Thomas Nelson och Sons, 1989.
3. Pinsent, m. Fysisk process. Storbritannien: Nelson Thomas, 2002.
4. Yadav, S K. Ingenjörsmekanik. Delhi: Discovery Publishing House, 2006.
5. Serway, R A och Jewett, J W. Fysik för forskare och ingenjörer. Kalifornien, USA: Brooks/Cole, 2010.