Förskjutna funktionsegenskaper, exempel, övningar

De förskjutad funktion y = s (x) är en funktion som definieras i delar eller av delar, så att det i ett ändligt intervall [a, b] har ett ändligt antal avbrott, som vi kommer att kalla x₀ < x₁ < x₂ <… . x_n.  I varje öppet intervall (x_Yo , x_I+1) och har ett konstant värde på värde s_Yo, Med diskontinuiteter -Saltos- vid punkter x_Yo.

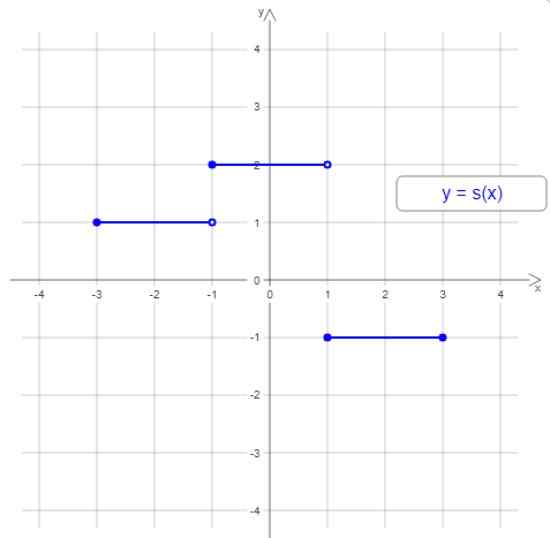
Grafen som är resultatet av en funktion som denna består av steg eller steg. Låt oss titta på ett exempel nedan:

Figur 1. Exempel på förskjuten funktion. Källa: Wikimedia Commons.

Grafen för denna stegade funktion har tre steg eller förskjutna intervaller, men i allmänhet kan den förskjutna funktionen ha någon mängd steg. Stegens bredd kan vara annorlunda och trappan är inte alltid stigande eller fallande.

Exemplets förskjutna funktion kan skrivas med att ange bredden och hög i varje steg, så här:

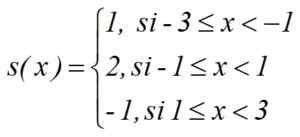
[TOC]

Egenskaper för den stegade funktionen

-Funktionen får sitt namn i grafen i form av steg, som ges av de segment som komponerar den. Varje segment har en del av funktionens domän och i var och en är funktionen konstant.

-Domänen för en förskjuten funktion är de värden som tillhör intervallet för vilket det definieras: [a, b], medan intervallet utgörs av värdena s_Yo av höjderna på trappan.

I exemplet i figur 1 är domänen intervallet [-3,3] och intervallet är värden -1, 1 och 2.

-Den förskjutna funktionen är kontinuerlig utom i de värden som avgränsar varje steg, punkterna x_Yo.

-Escalonada -funktioner kan läggas till och multipliceras för att ge upphov till nya stegade funktioner.

-Derivatet är 0 för de punkter där det definieras, eftersom funktionen i dem är konstant. Derivatet finns för sin sida inte i diskontinuiteter.

-Integralen i den stegade funktionen S (x) mellan till och b Det finns och motsvarar summan av områdena i rektanglarna i bredd x_Yo- x_I-1 och höjd s_k, lika med steget.

Kan tjäna dig: Oberoende evenemang: Demonstration, exempel, övningar

Eftersom området för en rektangel är produkten av basen efter höjd, måste vi:

Exempel på förskjutna funktioner

Inom de svängda funktionerna finns det flera typer, till exempel funktionerna i helhet och funktionen Enhetlig steg, liksom olika förskjutna funktioner som beskriver vanliga situationer, till exempel priser för många tjänster. Låt oss titta på några exempel:

- Exempel 1: Hela parterna

Hela delfunktionen använder ofta dubbelfäste:

f (x) = [[x]]

Och det definieras som en funktion som tilldelar varje verkligt nummer det närmaste eller mindre heltalet och ignorerar alla decimaler som har numret. I förekommande fall har vi:

Tak- eller himmelfunktion

Tilldelar varje domänvärde det närmaste heltalet av överskott. Till exempel:

[[+2.56]] = 3

Decimaldelen som är 0 ignoreras.56 och det närmaste heltalet tilldelas som är större än 2.

Ett annat exempel:

[[-4.2]]= -3

Återigen utelämnas decimaldelen 0.2 och det högsta största heltalet närmare -4 tas som ett värde på funktionen, vilket är -3.

I följande figur är grafen för takfunktionen, notera att steget avgränsas av en liten ihålig cirkel till vänster och en full till höger, eftersom valfritt antal av intervallet, det största heltalet tilldelas mellan ändarna mellan slutar mellan intervallets ändar.

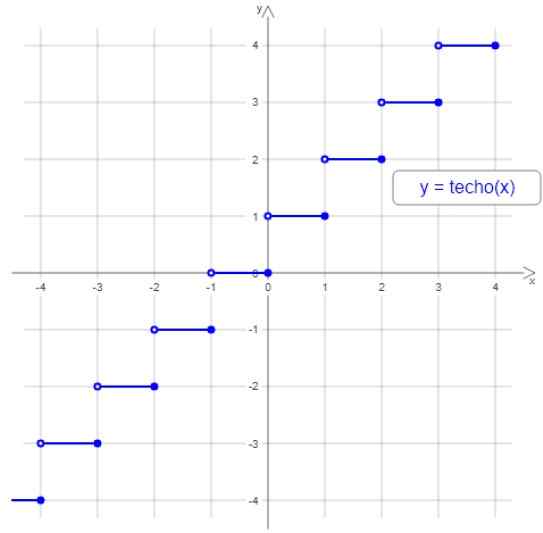figur 2. Taket eller himmelfunktionen. Källa: Wikimedia Commons.

Till exempel tilldelas alla värden mellan 3 och 4 hela 4, som är mellan -2 och -1 tilldelas -1 och så vidare.

Golv eller markfunktion

Tilldelar varje domänvärde det närmaste hela numret som standard. Exempel på denna funktion är:

Kan tjäna dig: hur många tiondelar finns det i en enhet?

[[+3.7]] = 3

[[-1.5]] = -2

[[π]] = 3

Båda funktionerna är kontinuerliga förutom hela siffror, där hopp presenteras, och det är konstant för värdena mellan heltal k och k+1.

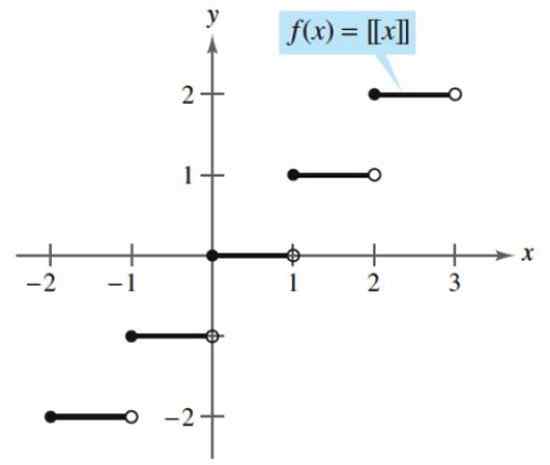Figur 3. Golv eller markfunktion. Källa: Larson, R. Beräkning av en variabel.

- Exempel 2

I en stad är taxibilen 3.65 $ för de första 100 m. Och för varje 100 m är 0.18 $, är gränsen per rutt på 50 km.

Det är önskvärt att fastställa funktionen som hänför sig till rutten i meter med kostnaden för tjänsten med $, som måste ha detta formulär:

f (x) = 3.65 + 0.18. [[x /100]] $

Där hela delfunktionen kan vara av himmelfunktionen, till vilken basfrekvensen är 3 läggs till.65 $. Om vi ​​till exempel vill veta hur mycket det kommer att betalas för en resa på 6.25 km = 6250 m, vi kommer att ha:

f (x) = 3.65 + 0.18. [[x /100]] $ = 3.65 + 0.18 . [[6250/100]] $ = 3.65 + [[11.25]] $ = 15.65 $

Om taxisföretaget väljer en golvfunktion, skulle klienten betala lite mindre för resan:

f (x) = 3.65 + 0.18. [[x /100]] $ = 3.65 + 0.18 . [[6250/100]] $ = 3.65 + [[11.25]] $ = 14.65 $

Löst övningar

- Övning 1

Långdistanssamtal mellan städer A och B kostar 0.40 $ 10 minuter. Efter den perioden är fraktionen eller ytterligare minut värt 0.05 $.

Uttryck kostnaden c (t) för ett samtal som varar en viss mängd minuter.

Lösning

Vi kan uttrycka den här funktionen om vi analyserar vad som händer med varje alternativ under ett samtal:

För t ≤ 10 minuter

När t, vilket är den tid som samtalet varar, är mindre än eller lika med 10 minuter, betalas 0.$ 40.

Kan tjäna dig: 2 -siffriga divisioner löst

Därför:

f (t) = 0.$ 40 för T ingår mellan 0 och 10 minuter.

Vi har redan en del av funktionen.

För t> 10 minuter

Entero T -fall

Låt oss nu se vad som händer när tiden för t = 10 minuter överskrids: det kan hända att överskottet är ett heltal, till exempel att konversationen varar exakt 11, 12, 13, 14 minuter eller mer. I så fall kommer beloppet för samtalet att vara:

f (t) = 0.40 + 0.05 (T-10) $, för T större än 10 minuter, med hela T.

Det vill säga att i detta fall: t = 11, 12, 13, 14, 15 ... minuter.

Anta till exempel att konversationen varar exakt 15 minuter, kostnaden kommer att vara:

f (15) = 0.40 + 0.05 (15-10) $ = 0.65 $

Decimalfall

Slutligen, överväg fallet där samtalet varar en tid med en decimaldel. Anta till exempel att samtalet varar 15 minuter och 45 sekunder, vilket skulle vara decimalt 15.75 minuter.

Vi kan uttrycka det i termer av hela delen av golvtypen, förutsatt att företaget vill ge fler fördelar för klienten eller himlen:

f (t) = 0.40 + 0.05 ⋅ [[T-9]] $

Låt oss se vad klienten skulle betala om det var en golvfunktion:

F (15.75) = 0.40 + 0.05 ⋅ [[15.75-9]] $ = 0.40 + 0.05⋅ [[6.75]] $ = 0.40 + 0.05 × 6 $ = 0.70 $.

Eller som en himmelfunktion, i så fall skulle kostnaden vara:

F (15.75) = 0.40 + 0.05 [[15.75-9]] $ = 0.40 + 0.05⋅ [[6.75]] $ = 0.40 + 0.05 × 7 $ = 0.75 $.

Funktion och grafik

Som en funktion som definieras av delar är:

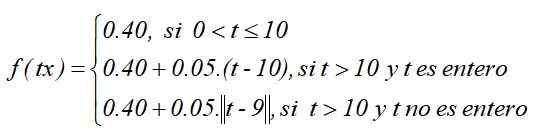
Funktionens graf skulle vara så här, förutsatt att hela taktypfunktionen valdes:

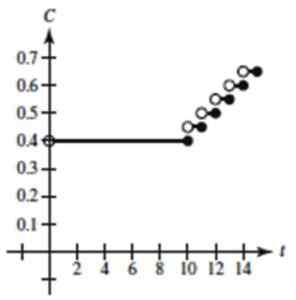Figur 4. Grafen över den stegade funktionen av övningen löstes 1. Källa: Larson, R. Beräkning av en variabel.

- Övning 2

Beräkna de integrerade ∫s (x) dx mellan -3 och 3 i den stegade funktionen:

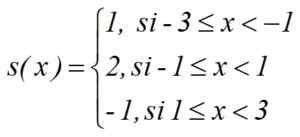
Lösning

Vi tillämpar definitionen för integralen av den förskjutna funktionen:

Därför är den integrerade sökte jag:

I = 1. [(-1)-(-3)] + 2.[1- (-1)]+(-1).[3-1] = 2+4-2 = 4

Referenser

1. Jiménez, r. 2006.Matematiska funktioner. Pearson Education.
2. Larson, r. 2010. Beräkning av en variabel. 9na. Utgåva. McGraw Hill.
3. Matematik IV. Funktioner. Återhämtat sig från: Cobaqroo.Edu.mx.
4. Wikipedia. Hela delfunktioner. Återhämtad från: är.Wikipedia.org.
5. Wikipedia. Förskjutad funktion. Återhämtad från: är.Wikipedia.org.