Homografisk funktion Hur man graferar, löste övningar

De fungeraHomografisk eller rationell Ón Det är en typ av matematisk funktion som består av uppdelningen av två polynomkomponenter. Det följer formen p (x)/q (x), där q (x) inte kan ta nollform.

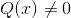
Exempelvis motsvarar uttrycket (2x - 1)/(x + 3) en homografisk funktion med p (x) = 2x - 1 y q (x) = x + 3.

Källa: Pixabay.com

Homografiska funktioner utgör en studieavsnitt av analytiska funktioner, som behandlas från graferingsmetoden och från domän- och intervallstudien. Detta beror på de begränsningar och stiftelser som måste tillämpas för deras resolutioner.

[TOC]

Vad är en homografisk funktion?

De är rationella uttryck för unik variabel, även om detta inte betyder att det inte finns något liknande uttryck för två eller flera variabler, där det redan skulle vara i närvaro av kroppar i rymden som följer samma mönster som den homografiska funktionen i nivån.

De har verkliga rötter i vissa fall, men förekomsten av vertikala och horisontella asymptoter upprätthålls alltid, liksom tillväxt och minskar intervall. Vanligtvis är bara en av dessa trender närvarande, men det finns uttryck som kan visa båda i deras utveckling.

Hans domän är begränsad av nämnarens rötter, eftersom det inte finns någon uppdelning mellan noll av verkliga siffror.

Blandad homografisk funktion

De är mycket frekventa i beräkningen, särskilt differentiell och omfattande, är nödvändiga för att härleda och anti -ängel under särskilda formler. Några av de vanligaste klassificeras nedan.

Nionde par av homografisk funktion

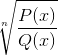
Utesluter alla element i domänen som gör argumentet negativt. Rötterna som finns i varje polynom visar nollvärden när de utvärderas.

Dessa värden accepteras av radikalen, även om den grundläggande begränsningen av den homografiska funktionen bör övervägas. Där q (x) inte kan ta emot nollvärden.

Kan tjäna dig: transcendenta funktioner: typer, definition, egenskaper, exempel

Intervalllösningar måste avlyssnas:

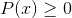
För att uppnå korsningar kan teckenmetoden användas bland andra.

Homografisk funktionslogaritm

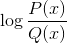
Utesluter domänvärden som kastar negativa intervaller och nollor. Eftersom nollorna redan är uteslutna från nämnaren, lösningarna av: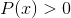

Det är också vanligt att hitta båda uttryck i en, bland andra möjliga kombinationer.

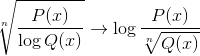
Hur man graferar en homografisk funktion?

Homografiska funktioner motsvarar grafiskt med hyperbolor i planet. Som transporteras horisontellt och vertikalt enligt de värden som definierar polynomerna.

Det finns flera element som vi måste definiera för att grafera en rationell eller homografisk funktion.

Egendom

Den första kommer att vara rötter eller nollor för funktionerna p och q.

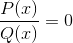
De uppnådda värdena kommer att betecknas på grafikens x -axel. Indikerar skärningspunkten i grafen med axeln.

Vertikal asymptot

Motsvarar vertikala linjer, som avgränsar grafen enligt de trender som de presenterar. De berör x -axeln i värdena som gör nämnaren noll och kommer aldrig att beröras av grafen för den homografiska funktionen.

Horisontell asymptot

Representerad av en horisontell sömlinje, avgränsade en gräns för vilken funktionen inte kommer att definieras vid den exakta punkten. Trender kommer att observeras före och efter denna linje.

För att beräkna det måste vi ta till en metod som liknar L'Hopital -metoden, som används för att lösa rationella funktioner som tenderar till oändlighet. Koefficienterna för de högsta krafterna i telleren och nämnaren för funktionen måste tas.

Till exempel har följande uttryck en horisontell asymptot vid y = 2/1 = 2.

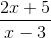
Tillväxtintervall

Värdena på de beställda kommer att ha trender markerade i grafen på grund av asymptoterna. När det gäller tillväxt kommer funktionen att öka från värden när elementen i domänen från vänster till höger utvärderas.

Kan tjäna dig: 60 delare

Minskande intervall

Beställda värden kommer att minska när elementen i domänen från vänster till höger utvärderas.

Hopparna som finns i värdena kommer inte att beaktas när ökar eller minskar. Detta inträffar när grafen är nära en vertikal eller horisont.

Korsning med y

Att göra noll till värdet på x, är skärningspunkten med ordinatens axel. Detta är ett mycket användbart faktum för att få grafen för den rationella funktionen.

Exempel

Definiera grafen för följande uttryck, hitta dess rötter, vertikala och horisontella asymptoter, tillväxt och minska intervaller och skärningspunkt med den beställda axeln.

Övning 1

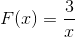
Uttrycket saknar rötter, eftersom det har ett konstant värde i telleren. Begränsningen att tillämpa kommer att vara x skiljer sig från noll. Med horisontell asymptot vid y = 0 och asymptot vertikal vid x = 0. Det finns inga skärningspunkter med axeln och.

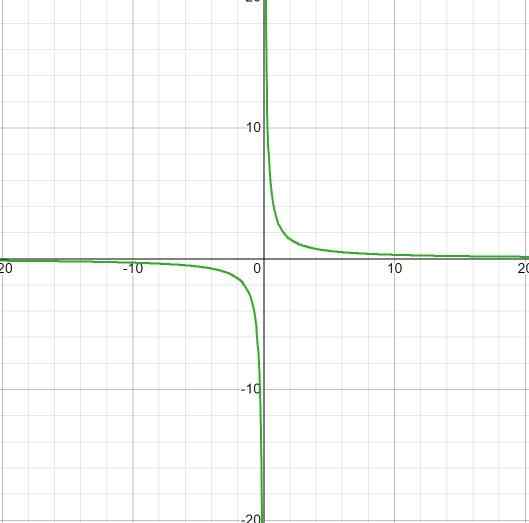
Det observeras att det inte finns några tillväxtintervall även med hoppet från mindre till mer oändligt i x = 0.

Minskningsintervallet är

Id: (-∞; o) u (0, ∞)

Övning 1.2

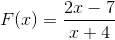
2 polynomer observeras som i den första definitionen, så vi fortsätter enligt de etablerade stegen.

Roten som hittades är x = 7/2 som är resultatet av att utjämna funktionen.

Den vertikala asymptoten är vid x = - 4, vilket är värdet som utesluts från domänen på grund av det rationella funktionstillståndet.

Den horisontella asymptoten är i y = 2, detta efter att ha delat 2/1, koefficienterna för grad 1 -variablerna.

Den har en korsning med de som beställs vid y = - 7/4. Värde hittades efter utjämning av x till noll.

Det kan tjäna dig: fraktion motsvarande 3/5 (lösning och förklaring)

Funktionen växer ständigt, med ett hopp från mer till mindre oändligt runt roten x = -4.

Dess tillväxtintervall är (-∞, - 4) u ( - 4, ∞).

När värdet på X är nära mindre oändligt tar funktionen värden nära 2. Detsamma händer när X närmar sig mer oändligt.

Uttrycket närmar sig mer oändligt när det utvärderas i - 4 till vänster och mindre oändligt när det utvärderas i - 4 till höger.

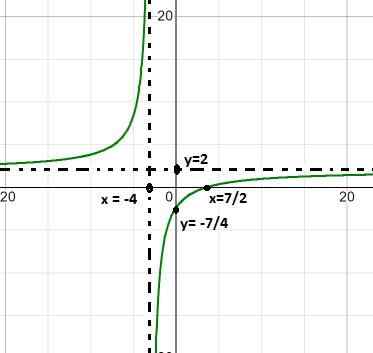
Övning 2

Grafen för följande homografiska funktion observeras:

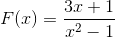
Beskriv deras beteende, rötter, vertikala och horisontella asymptoter, tillväxt och minska intervaller och skärningspunkt med den ordnade axeln.

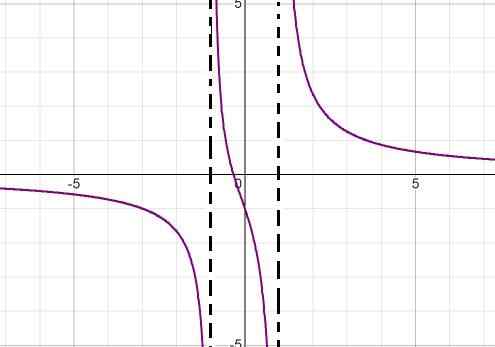
Uttrycket nämnaren indikerar genom att ta hänsyn till skillnaden mellan rutor (x + 1) (x - 1) rötternas värden. På detta sätt kan båda vertikala asymptoter definieras som:

x = -1 och x = 1

Den horisontella asymptoten motsvarar Abscissas axel eftersom den stora kraften är i nämnaren.

Dess enda rot definieras av x = -1/3.

Uttrycket minskar alltid från vänster till höger. Det närmar sig noll när det tenderar att oändligt. Mindre oändligt när du närmar sig -1 till vänster. Mer oändlig när du närmar sig -1 till höger. Mindre oändlig när du närmar sig 1 till vänster och mer oändlighet när du närmar sig 1 till höger.

Referenser

1. Approximation med rationella funktioner. Donald J. Ny man. Amerikansk matematisk SOC., 31 december. 1979
2. Ortogonala betygsfunktioner. University of La Laguna Tenerife Adhemar Bultheel, Adhemar Bultheel, Pablo Gonzalez-Vera, Erik Hendriksen, Olav Njstad. Cambridge University Press, 13 februari. 1999
3. Betyg om tillnärmning av verkliga funktioner. P. P. Petrushev, Vasil Atanasov Popov. Cambridge University Press, 3 mars. 2011
4. Algebraiska funktioner. Gilbert Ames Bliss. Couer Corporation, 1 jan. 2004
5. Spanska Matematical Society Magazine, 5-6 volymer. Spanish Mathematical Society, Madrid 1916