Verklig verklig variabel funktion och dess grafiska representation

En verklig verklig variabel funktion Ta ett antal som tillhör uppsättningen av verkliga siffror och associerar det till ett annat värde, också verkligt, genom en unik korrespondensregel. Detta innebär att det verkliga numret får genom denna regel en unik bild.

Numeriska avgångsvariabler betecknas vanligtvis med bokstav X, medan deras bild är bokstaven och. Å andra sidan kallas till korrespondensregeln som länkar dem också med någon annan bokstav i alfabetet, till exempel "F" -funktionen, även om en annan kan användas.  I kompakt notation är det skrivet:

f: x → y = f (x)

Figur 1. Graf över en verklig polynomfunktion

Till variabeln  x det kallas oberoende variabel, medan och Det är beroende variabel. Funktionen kan uttryckas på flera sätt, till exempel genom ett matematiskt uttalande som dessa:

• f (x) = 2x −3
• H (x) = −3x²
• 

En annan uttrycksform är genom en graf, vilket är mycket användbart eftersom det gör att du kan uppskatta beteendet hos funktionen hos en enda blick. Att bygga en graf är mycket enkel med hjälp av ett kartesiskt koordinatsystem, där kamrater [x, f (x)] representeras som punkter i planet. Sedan går de samman med en mjuk och kontinuerlig linje, du kan se hur funktionen är.

Exempel

För att bygga grafen kan du ta till en tabell över värden där punkterna till grafen är placerade. För variabla X -värden väljs som tillhör funktionens domän, det vill säga de som när de ersätts i formeln, i sin tur visar verkliga siffror.

När värdena på x har valts bestäms dess bild y = f (x), och på detta sätt erhålls punkterna par [x, f (x)] som kommer att vara grafiska.

Kan tjäna dig: Homografisk funktion: Hur man graferar, löste övningar

Det finns några punkter som är viktiga och bör inkluderas i tabellen: de där grafen skär till koordinataxlarna, att om de finns, eftersom inte alla funktioner korsar dem.

För att beräkna dem, fortsätt enligt följande:

-Korsning med axeln och: x = 0 tillverkas i funktionsformeln och motsvarande värde beräknas.

-Korsning med x -axeln: Y = 0 är klar och ekvationen f (x) = 0 löses.

Därefter ritas det kartesiska koordinatsystemet och var och en av punkterna planeras, som sedan förenas med en mjuk och kontinuerlig linje om möjligt.

Exempel 1

Bygg en tabell med värden och grafen för följande funktion:

f (x) = x² −4

Innan du börjar måste du hitta domänen för funktionen, som är uppsättningen av verkliga värden som funktionen finns. Eftersom det är en kvadratisk funktion, har alla X -värde som tillhör de verkliga siffrorna en verklig bild, enligt F (X).

Sedan kan tabellen byggas genom att välja valfritt x -värde, och det enklaste är att börja med skärningspunkten i grafen med axlarna, om det finns. Efter att ha hittat dem försöker andra punkter att slutföra tabellen.

För x = 0

f (0) = -4

Därför är den första punkten i tabellen (0, -4). Detta är skärningspunkten mellan grafen med axeln och.

För y = 0

Sedan är y = 0 klar och ekvationen som resultat löses:

x² −4 = 0

x² = 4

Lösningarna på denna ekvation är: x₁= 2 och x₂= -2. Därför finns det två korsningar med X -axeln, som är punkterna: (−2.0) och (2.0).

Kan tjäna dig: perfekta siffror: hur man identifierar dem och exempel

Nu kan du hitta fler poäng att lägga till i värdena:

För x = 1

f (1) = (1)² - 4 = −3

För x = - 1

f (−1) = (−1)² - 4 = −3

För x =  3

f (3) = (3)² - 4 = 5

För x =  -3

f (−3) = (−3)² - 4 = 5

Värdesabell

Följande tabell visar de erhållna punkterna, som kommer att tjäna till att bygga grafen för f (x):

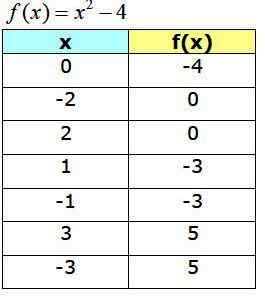Funktionsgraf f (x) = x² −4

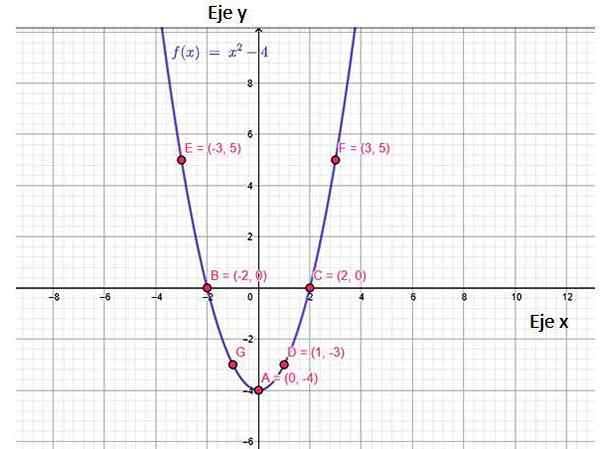figur 2. Funktion f (x) funktionsgraf, visar några punkter som tillhör den, inklusive korsningar med axlar. Källa: f. Zapata, genom Geogebra.

Grafen för den här funktionen är en liknelse, som öppnas och har en minsta punkt, kallad vertex, av koordinater (0, −4). Det är intressant att notera att värdena på f (x) börjar vid y = -4 till ∞. Detta är räckvidden av funktionen.

Av grafen kan man dra slutsatsen att funktionen är kontinuerlig, minskar i intervallet (−∞, 0) och ökar därifrån.

Exempel 2

Att ha diagrammet över funktionen är det möjligt att känna till dess domän, dess intervall, korsningarna det har med axlarna och visualisera dess allmänna beteende (tillväxt och minskning).

Nedan är grafen för polynomfunktionen:

f (x) = - x⁴+4x²+1

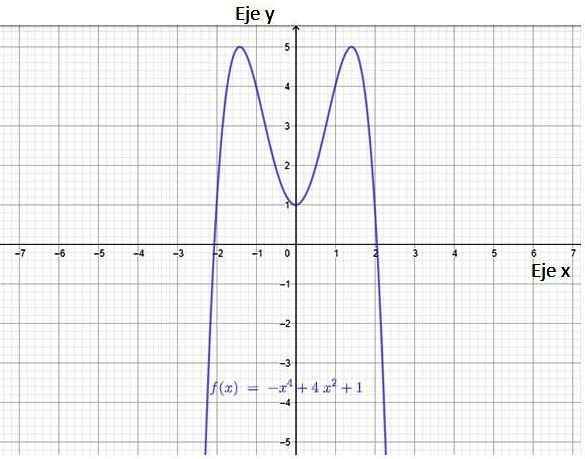Figur 3. Graf över en polynomfunktion. Källa: f. Zapata genom geogebra.

Från bilden följer att funktionen har två korsningar med X-axeln, punkterna (-2.0) och (2.0). Den har också en korsning med Y -axeln, punkten (0,1).

Domänen för en polynomfunktion är den kompletta uppsättningen av verkliga siffror, det varnas också för att funktionen är kontinuerlig och har symmetri runt den vertikala axeln. Det kan verkligen verifieras att den här funktionen är Symmetri för. En funktion är även om den uppfyller:

Kan tjäna dig: grönt teorem, demonstration, applikationer och övningar

f (x) = f (-x)

Läsaren kan verifiera att genom att ersätta -x i funktionen ändras den inte.

Det finns två intressanta punkter, som är på höjden av y = 5, är de maximala värdena på funktionen. Området för denna funktion, det vill säga uppsättningen värden som variabeln tar och sträcker sig från -∞ till y = 5 exakt.

För att känna till värdena på X vars bild är y = 5, ersätts detta värde i funktionen:

5 = - x⁴+4x²+1

Och denna ekvation erhålls:

- x⁴ + 4x² - 4 = 0

Vars lösningar är −√2 och + √2. Tja, funktionen är:

-Växande Från x -∞ till x = −√2

-Minskande Från x = −√2 till x = 0

-Växande Från x = 0 till x = + √2

-Minskande Från x = + √2 och framåt.

Träning löst

Bygg grafen för följande funktion:

f (x) = √ (x-5)

Lösning

Först måste du bestämma funktionens domän, att veta vilka värden på X som kan väljas för att bygga tabellen. När det gäller den föreslagna funktionen måste beloppet inom roten alltid vara positiv eller lika med 0, därför:

x - 5 ≥ 0

x ≥ 5

Därför kan endast värden större än eller lika med 5 väljas för bordet. När det gäller korsningar med koordinataxlarna är den enda möjligheten att göra y = 0 och sedan x = 5.

Det är värdelöst att göra x = 0 för denna funktion, eftersom detta värde inte tillhör domänen.

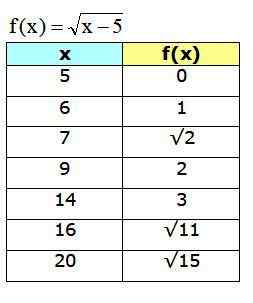
Grafen som erhålls är:

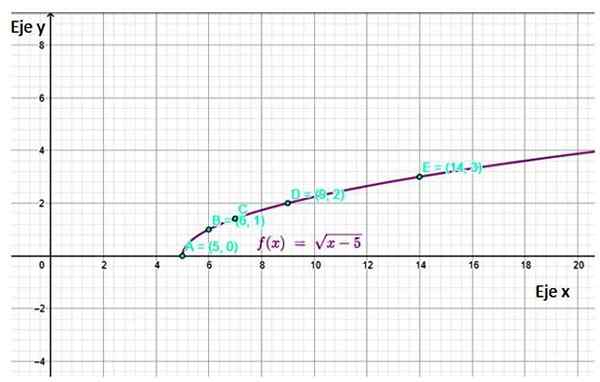Figur 4. Funktionsgraf f (x) Visar några av de punkter som beräknas i tabellen. Källa: f. Zapata genom geogebra.

Referenser

1. E-math zon. Typer av funktioner. Återhämtat sig från: Emathzone.com.
2. Hoffman, J.G. Urval av matematikfrågor. Ed. Spphinx.
3. Matematik är kul. Commons Functions Reference. Återhämtat sig från: Mathisfun.com.
4. Requena, b. Universumsformler. Typer av funktioner. Återhämtat sig från: universalformulor.com.
5. Stewart, J. 2006. Preccculment: Matematik för beräkning. Femte. Utgåva. Cengage Learning.