Examensfunktioner större än två (exempel)

A (polynom) av klass större än två har den allmänna formen:

f (x) = a₀ + till₁x +a₂x² +.. .till_nxⁿ

Med n = 3, 4, 5, ..., ett icke -negativt heltal och koefficienterna till_antingen, till₁Till ... till_n, som vanligtvis är riktiga siffror.

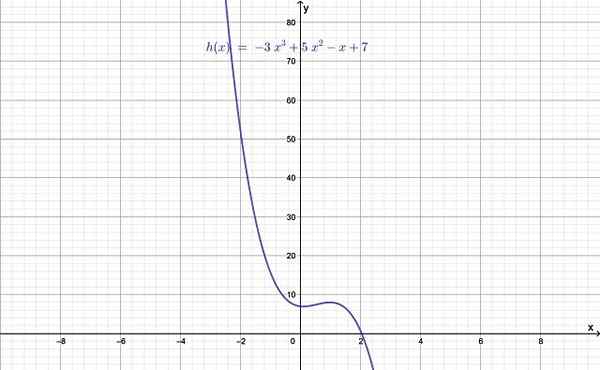Figur 1.- Graf över en examensfunktion större än 2. Källa: f. Zapata.

Graden av funktionen ges av värdet på N, den största av exponenterna och som i sin tur är större än 2. När n = 0 är en konstant funktion, om n = 1 är det en linjär funktion, och slutligen med n = 2 är det en kvadratisk funktion.

Exempel på funktioner på mer än två, i variabeln "X", är följande:

• f (x) = x³
• H (x) = - 3x³ + 5x² - X + 7
• g (x) = x⁴ - 6x² + 25

Funktionen f (x) = x³ Det är det enklaste av alla funktioner i större än två och dess examen är 3. En examen 3 kallas också kubikfunktion. För sin del är G (x) klass 4, för att vara 4 den maximala exponenten.

Värdet på N är mycket viktigt eftersom det bestämmer den allmänna formen för grafen, och även den maximala mängden rötter eller korsningar som funktionen har med den horisontella axeln. Faktum är att en 3 -graders funktion kommer att beröra den horisontella axeln högst 3 punkter, en av klass 4 kommer att göra det högst i fyra poäng och så vidare.

När det gäller den oberoende termen, i en polynomfunktion i någon grad indikerar det skärningspunkten mellan funktionen med den vertikala axeln.

Egenskaper hos polynomfunktionerna i större än två

Domän

Domänen för en funktion är uppsättningen värden som möjliggör beräkning av värdena på y = f (x). För polynomfunktioner är denna uppsättning den av verkliga n -nummer, eller uppsättningen av komplexa nummer, om det behövs för att utöka domänen.

Kan tjäna dig: trigonometriska gränser: hur man löser dem, lösta övningar

Betyder att med tanke på polynomfunktionen f (x) = a₀ + till₁x +a₂x² +.. .till_nxⁿ, Du kan alltid ersätta alla verkliga nummer, utföra de angivna operationerna och få ett resultat ett värde av verklig y = f (x) verklig.

Räckvidd

Det är uppsättningen som bildas av alla förvärvade värden f (x), det vill säga de bilder som varje värde på x har genom funktionen f (x). För polynomfunktioner större än 2 är denna uppsättning den av verkliga siffror.

Rötter till funktionen

Är värdena på x för vilka det uppfylls att f (x) = 0. Som anges ovan indikerar funktionen graden det maximala antalet rötter som det kan ha, även om inte alla är nödvändigtvis verkliga.

När funktionskoefficienterna är verkliga siffror motsvarar de verkliga rötterna korsningarna i funktionen med X -axeln.

Exempel 1

De rationella rötterna för funktionen f (x) = 2x³ - 9x² + 7x + 6 kan hittas genom följande sats:

Om roten till f (x) = a₀ + till₁x +a₂x² +.. .till_nxⁿ Det är B/C -formen, så de möjliga värdena för B är faktorer för a_antingen och de möjliga värdena för C är faktorer för a_n.

För exemplets funktion är de redan förenklade kombinationerna: ± 6, ± 3, ± 2, ± 1, ± 3/2, ± ½. Nu testas var och en genom syntetisk uppdelningsprocedur, till exempel. När divisionsrester är 0 är det beprövade värdet en rot:

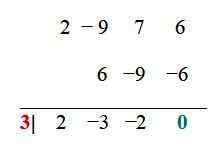
Värdet x₁ = 3 är en rot eller noll av funktionen, därför (x - 3) är en vanlig faktor för f (x), och detta kan skrivas som:

Det kan tjäna dig: Unitary Circle: Trigonometric Functions and Applications

f (x) = (x - 3) ∙ (2x² −3x −2)

De återstående två rötterna är värdena som uppfyller 2x -ekvationen² −3x −2 = 0. Denna ekvation kan lösas genom den allmänna formeln, en vetenskaplig kalkylator eller upprepa den tidigare Tanteo -processen.

Dessa rötter är x₂ = 2 och x₃ = - ½, och nu kan f (x) skrivas som produkten av tre faktorer:

f (x) = (x - 3) ∙ (x - 2) ⋅ (x + ½)

Korsningarna mellan f (x) med x -axeln är punkterna: p₁ (3.0), s₂(2.0) och P₃(−½, 0). Grafen över funktionen, erhållen med Geogebra, visar dess korsningar med X -axeln:

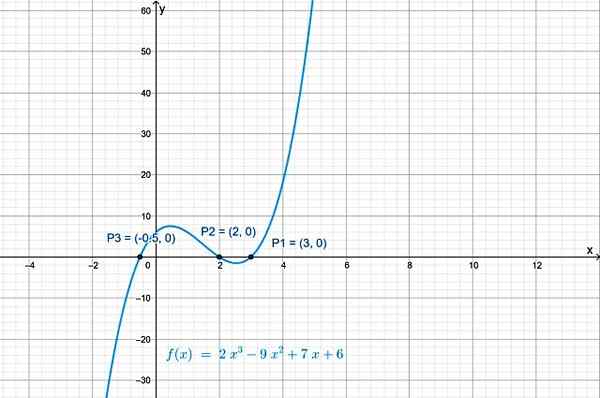figur 2.- En polynomfunktion i grad 3 har tre korsningar med den horisontella axeln. Källa: f. Zapata.

Korsning med den vertikala axeln

För att hitta skärningspunkten mellan funktionen med den vertikala axeln måste du hitta f (0), vilket helt enkelt är till₀.

Exempel 2

Hitta skärningspunkten mellan f (x) = 2x³ - 9x² + 7x + 6 Med den vertikala axeln är den väldigt enkel när du gör x = 0 i f (x) det erhålls:

f (x) = 6

Och skärningspunkten för funktionen med den vertikala axeln är P₄(0,6).

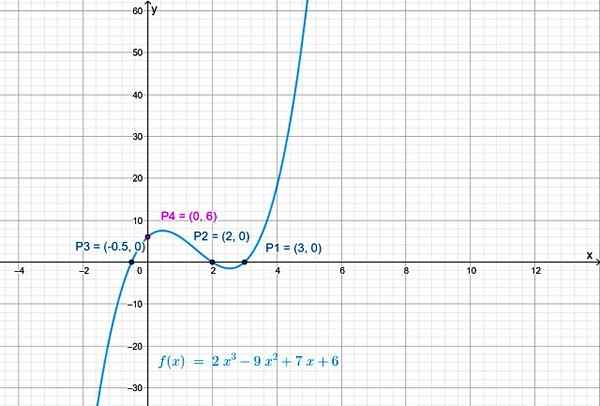Figur 3. Korsningen mellan kurvan med den vertikala axeln gör x = 0 i f (x). Källa: f. Zapata.

Kontinuitet

Polynomfunktioner i allmänhet, och i synnerhet de med högre än 2 är kontinuerliga funktioner i hela deras domän, betyder detta att de inte har några hopp, steg, hål eller värden för vilka de inte definieras. De har inte heller asymptoter, som är vertikala, horisontella eller sned raka som funktionen närmar sig utan att korsa dem.

Dessa egenskaper av mjukhet och kontinuitet uppskattas i graferna som visas ovan.

Graf över funktioner högre än 2

Graferna för funktionerna högre än 2 är kontinuerliga och mjuka, och deras form beror på graden av polynomet.

Kan tjäna dig: permutationer utan upprepning: formler, demonstration, övningar, exempel

Till exempel, de i grad 3 Ream, det har ett negativt tecken på termen med högsta grad).

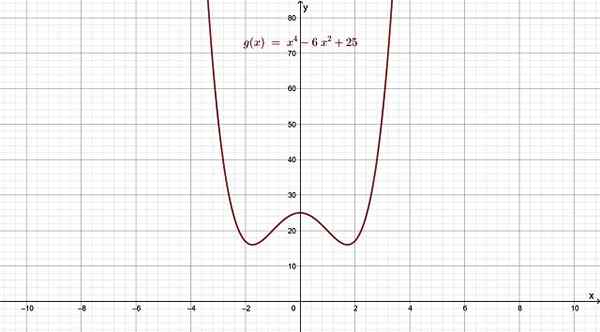Figur 4. Polyinomisk funktion av grad 4, vars graf liknar en bokstav w. Källa: f. Zapata.

För värden på x bort från x = 0, både vänster och höger, uppför funktionen hur termen av största grad skulle göra, eftersom detta råder över andra när x blir mycket stor eller mycket liten.

På bilden som följer funktionen F (x) = 2x jämförs³ - 9x² + 7x + 6 med funktionen r (x) = x³ Och det uppskattas att formen på båda kurvorna liknar värden på x som är långt långt ifrån x = 0.

För stora X -värden växer funktionen snabbt genom att tendera till +∞, medan för negativa X -värden minskar funktionen snabbt och tenderar att −∞.

Figur 5.- Alla N -funktioner beter sig på samma sätt när de rör sig bort från x = 0, både vänster och höger. Källa: f. Zapata.

Jämförelse av vridmomentskurvor (figur 4) med den udda graden (figur 2), så länge koefficienten som åtföljer den högsta kvalitetsperioden har samma tecken, observeras att de udda gradskurvorna börjar från "Y" negativt och växa, medan de i målgraden börjar i "y" positivt och minskar.

Referenser

1. Barnett, r. 2000. Preccculment: Funktioner och grafik. 4th. Utgåva. McGraw Hill.
2. Beräkning.Likström. Polynomfunktioner. Återhämtad från: beräkning.Likström.
3. Larson, r. 2012. Förkalkning. 8th. Utgåva. Cengage Learning.
4. Stewart, J. 2007. Preccculment: Matematik för beräkning. Femte. Utgåva. Cengage Learning.
5. Varsity tutrorrs. Grafering av polynomfunktioner. Hämtad från: WarsityTorm.com.