Omvända trigonometriska funktioner, härledda, exempel, övningar

De Omvända trigonometriska funktioner, Som namnet antyder är de motsvarande omvända funktioner för sinus, kosinus, tangent, cotangent, torkning och skördarefunktioner.

Omvända trigonometriska funktioner betecknas med samma namn på dess motsvarande direkta trigonometriska funktion plus prefixet BÅGE. Således:

1.- Bågen (x) Det är den omvända trigonometriska funktionen hos funktionen synd (x)

2.- Arccos (x) Det är den omvända trigonometriska funktionen hos funktionen cos (x)

3.- Arctan (x) Det är den omvända trigonometriska funktionen hos funktionen Solbrun (x)

4.- Arccot ​​(x) Det är den omvända trigonometriska funktionen hos funktionen barnsäng (x)

5.- Arcsec (x) Det är den omvända trigonometriska funktionen hos funktionen sec (x)

6.- Arccsc (x) Det är den omvända trigonometriska funktionen hos funktionen CSC (x)

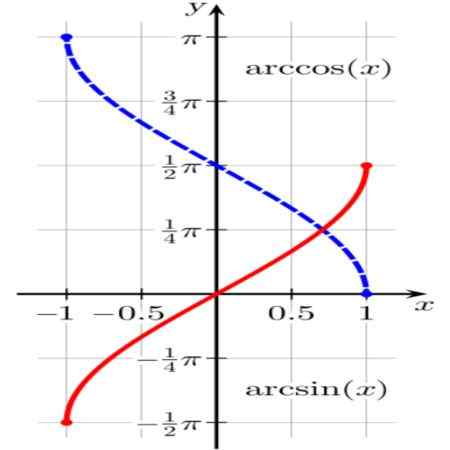
Figur 1. Arcsen -funktioner (x) (i rött) och arccos (x) (i blått). Källa: Wikimedia Commons.

Funktionen θ = arcsen (x) Det resulterar i en enhet båge θ (eller vinkel i radianer θ) Så att synd (θ) = x.

Således, till exempel, bågen (√3/2) = π/3 Eftersom som är känt är bröstet av π/3 -radianer lika med √3/2.

[TOC]

Huvudvärdet för omvända trigonometriska funktioner

Så att en matematisk funktion f (x) har omvänd g (x) = f^-1(x) Det är nödvändigt att denna funktion ska vara Injicering, Vilket innebär att varje värde och ankomstuppsättningen för funktionen f (x) kommer från en och endast ett x -värde.

Det är uppenbart att detta krav inte uppfylls av någon trigonometrisk funktion. För att klargöra poängen, låt oss märka att värdet y = 0,5 kan erhållas från sinusfunktionen på följande sätt:

• synd (π/6) = 0,5
• synd (5π/6) = 0,5
• synd (7π/6) = 0,5

Och många fler, eftersom sinusfunktionen är periodisk med period 2π.

Det kan tjäna dig: multiplar på 8: Vad är och förklaring

För att definiera omvända trigonometriska funktioner är det nödvändigt att begränsa domänen för deras motsvarande direkta trigonometriska funktioner, så att de uppfyller injektivitetskravet.

Denna begränsade domän för direkt funktion kommer att vara huvudområdet eller grenen för dess motsvarande omvända funktion.

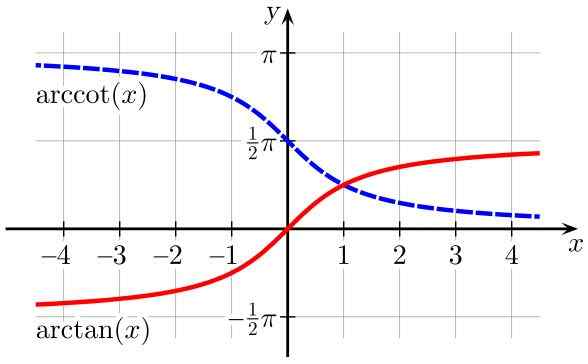figur 2. Arctan -funktioner (x) (i rött) och arccot ​​(x) (i blått). Källa: Wikimedia Commons.

Tabell över domäner och intervall av omvända trigonometriska funktioner

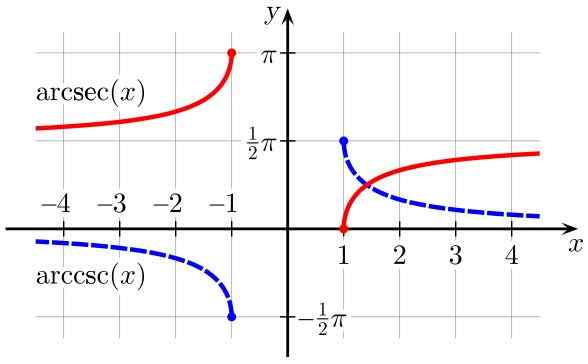Figur 3. ArcSec (x) (i rött) och arccsc (x) (i blått) funktioner (i blått). Källa: Wikimedia Commons.

Härrörande från omvända trigonometriska funktioner

För att erhålla derivat av de omvända trigonometriska funktionerna appliceras egenskaperna hos derivaten, särskilt den som härrör från en omvänd funktion.

Om vi ​​anger för f (y) till funktionen och av f^-1(x) till dess omvända funktion, då är det härrörande från den omvända funktionen relaterat till derivatet av direkt funktion genom följande förhållande:

[F^-1(x)] '= 1/ f' [f^-1(x)]

Till exempel: om x = f (y) = √y är den direkta funktionen kommer dess omvända att vara

y = f^-1(x) = x². Låt oss tillämpa regeln om det omvända derivatet på detta enkla fall för att se att denna regel uppfylls:

[x²] '= 1 / [√y]' = 1 / (½ och^-½ = 2 och^½ = 2 (x²)^½ = 2x 

Vi kan bedöma detta trick för att hitta de härledda från omvända trigonometriska funktioner.

Till exempel tar vi θ = arcsen (x) Som den direkta funktionen kommer dess omvända funktion att vara synd (θ) = x.

[arcsen (x)] '= 1 / [sin (θ)]' = 1 / cos (θ) = 1 / √ (1 - sen (θ)²) = ..

... = 1 / √ (1 - x²) .

På detta sätt kan alla de härrörande från de omvända trigonometriska funktionerna erhållas, som visas nedan:

Figur 4. Tabell över de härrörande från omvända trigonometriska funktioner. Källa: Wikimedia Commons.

Dessa derivat är giltiga för alla z -argument som tillhör komplexa siffror och är därför också giltiga för alla verkliga argument x, eftersom z = x + 0i.

Kan tjäna dig: fyrkantig: element, egenskaper, klassificering, exempel

Exempel

- Exempel 1

Hitta Arctan (1).

Lösning

Arctan (1) är enhetsbågen (vinkel i radianer) ፀ så att solbränna (ፀ) = 1. Den vinkeln är ፀ = π/4 eftersom så (π/4) = 1. Sedan Arctan (1) = π/4.

- Exempel 2

Beräkna Arcsen (cos (π/3)).

Lösning

Vinkeln π/3 -radianerna är en anmärkningsvärd vinkel vars kosinus är ½, så att problemet reduceras till att hitta arcsen (½).

Så det handlar om att hitta vinkeln vars sinus ger ½. Den vinkeln är π/6, eftersom sen (π/6) = sen (30º) = ½. Därför arcsen (cos (π/3)) = π/6. 

Övningar

- Övning 1

Hitta resultatet av följande uttryck:

Sec (Arcan (3)) + CSC (Arccot ​​(4))

Lösning

Vi börjar namnge a = arcan (3) och β = arcot (4). Så uttrycket vi måste beräkna är så här:

SEC (α) + CSC (ß)

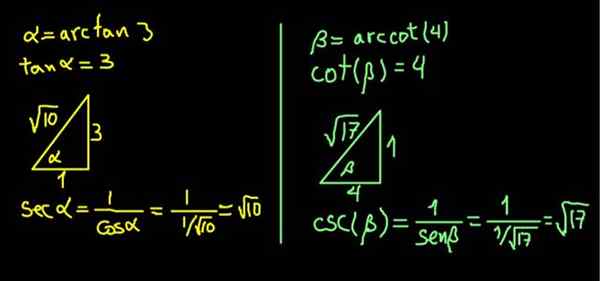
Uttrycket α = arcan (3) motsvarar att säga så (α) = 3.

Eftersom tangenten är det motsatta benet på det intilliggande, byggs en rektangel triangel av Cateto motsatt till a av 3 enheter och en angränsande kategori på 1 enhet, så att SO (α) = 3/1 = 3.

I en rektangelstriangel bestäms hypotenusen av Pythagoras teorem. Med dessa värden är det √10, så att:

Sec (α) = hypotenus / intilliggande kateto = √10 / 1 = √10.

På liknande sätt är β = arcot (4) motsvarande att ange att barnsäng (β) = 4.

En rektangel triangel av kateto intill ß av 4 enheter och en motsatt kateto på 1 enhet byggs, så att barnsängen (β) = 4/1.

Triangeln är omedelbart klar att hitta sin hypotenus tack vare Pythagoras teorem. I det här fallet visade det sig ha √17 enheter. Sedan beräknas CSC (ß) = hypotenus / motsatt kateto = √17 / 1 = √17.

Det kan tjäna dig: y = 3sen (4x) funktionsperiod

Att komma ihåg att uttrycket vi måste beräkna är: 

Sec (Arcan (3)) + CSC (Arcot (4)) = sec (α) + CSC (β) = ..

... = √10 + √17 = 3,16 + 4,12 = 7,28.

- Övning 2

Hitta lösningarna på:

Cos (2x) = 1 - sen (x)

Lösning

Det är nödvändigt att alla trigonometriska funktioner uttrycks i samma argument eller vinkel. Vi kommer att använda identiteten på den dubbla vinkeln:

Cos (2x) = 1 - 2 sen²(x)

Sedan reduceras det ursprungliga uttrycket till:

1 - 2 sen²(x) = 1 - sin x

När den är förenklad och faktoriserad uttrycks det som:

sin (x) (2 sen (x) - 1) = 0

Vilket ger upphov till två möjliga ekvationer: sin (x) = 0 med lösning x = 0 och en annan ekvation sen (x) = ½ med x = π/6 som en lösning.

Lösningarna på den uppförda ekvationen är: x = 0 eller x = π/6.

- Övning 3

Hitta lösningarna för följande trigonometriska ekvation:

cos (x) = sin²(x)

Lösning

För att lösa denna ekvation är det bekvämt att placera en enda typ av trigonometrisk funktion, så vi kommer att använda den grundläggande trigonometriska identiteten så att den ursprungliga ekvationen skrivs om enligt följande:

cos (x) = 1 - cos²(x)

Om vi ​​namnger y = cos (x) kan uttrycket skrivas om som:

och² + och - 1 = 0

Det är en andra gradsekvation i och vars lösningar är:

y = (-1 ± √5) / 2

Då är värdena på X som uppfyller den ursprungliga ekvationen:

x = Arcos ((-1 ± √5) / 2)

Den verkliga lösningen är det positiva tecknet x = 0,9046 rad = 51,83º.

Den andra lösningen är komplex: x = (π - 1.06 i) rad.

Referenser

1. Hazewinkel, m. 1994. Encyclopaedia of Mathematics. Kluwer Academic Publishers / Springer Science & Business Media. 
2. Mobilkamrat. Omvända trigonometriska funktioner. Återhämtad från: Matemovil.com
3. Universumsformler. Omvända trigonometriska funktioner. Återhämtat sig från: universalformulor.com
4. Weisstein, Eric W. Uppfinna trigonometriska funktioner. Återhämtat sig från: Mathworld.Volfram.com
5. Wikipedia. Uppfinna trigonometriska funktioner. Hämtad från: i.Wikipedia.com