Matematik

Vektorfunktioner

Vad är vektorfunktioner?

En vektorfunktion av en parameter t, Det är en funktion vars domän är de verkliga värdena på t, Medan rutten bildas av vektorer i formen r (t). En sådan funktion kan uttryckas som:

r (t) = f (t) Yo + g (t) J + H (t) k

Var Yo, J och k De är enhetsvektorerna i de tre huvudriktningarna i rymden, och funktionerna f, g och h är verkliga funktioner för variabeln t. Notationen använder sig av djärva, för att skilja vektorstorlekar.

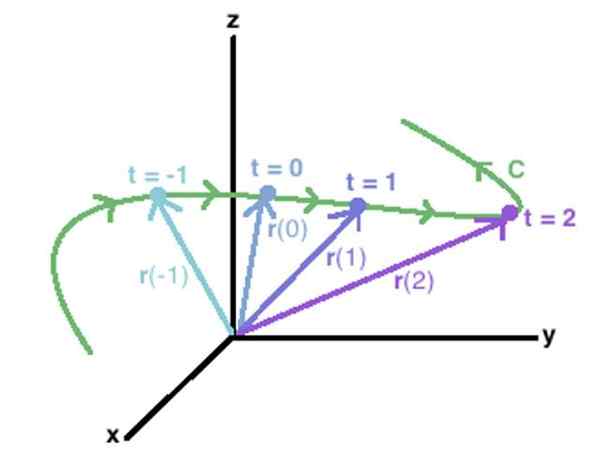En vektorfunktion i rymden kan användas för att beskriva en C -kurva och gå med de extrema punkterna för var och en av vektorerna som bestäms av nämnda funktion. Källa: Wikidot.

Ett annat sätt att beteckna en vektorfunktion är genom fyrkantiga parenteser:

r (t) = t), G (t), H (t)>

Vektorfunktioner kan användas för att studera kurvor i planet och rymden, till exempel banan som följer ett rörligt objekt. Ett exempel är den liknelse som beskrivs av en projicerad boll med initial hastighet, under tyngdkraften.

Om du vill veta bollens position vid varje ögonblick t, Vektorfunktionen med två komponenter, en horisontell och en vertikal:

r (t) = x (t) Yo + och(t) J

Båda x (t) som y (t) De är tidsfunktioner t. Således, när du går med i de extrema punkterna för var och en av vektorerna r(t) Möjligt, bilda liknelsen som beskrivs av bollen i planet Xy.

Konceptet sträcker sig lätt till en C -kurva i rymden, till exempel den som visas i figuren ovan. Vektorer visas i den r (-1), r (0), r (1) r (2), vars ändar drar C -kurvan, ritad i grönt.

Gränser, härledda och integrerade vektorfunktioner

Beräkningsverktyg som gäller verkliga verkliga variabla funktioner kan också tillämpas på vektorfunktioner.

Kan tjäna dig: faktorisering

Gränsen för en vektorfunktion

Vektorfunktionsgränsen r (t) = f (t) Yo + g (t) J + H (t) k, När T → A definieras som:

$\dpi110 \displaystyle \lim_t \to a\textbfr(t)=\left [ \displaystyle \lim_ t\to a f(t)\right ]\textbfi+\left [ \displaystyle \lim_ t\to a g(t)\right ]\textbfj+\left [ \displaystyle \lim_ t\to a h(t)\right ]\textbfk$

Förutsatt att det finns respektive gränser för F (t), G (t) och h (t), när t → a.

Härrörande från en vektorfunktion

Definitionen av härrörande från en vektorfunktion r (t) = f (t) Yo + g (t) J + H (t) k Det är analogt med derivatet av en verklig funktion av verklig variabel. Kallelse r'(t) till nämnda derivat har du:

$\dpi110 \mathbfr'(t)=\displaystyle \lim_\Delta t \to 0\frac\mathbfr(t+\Delta t)-\mathbfr(t)\Delta t$

Derivatet finns när den föregående gränsen finns, och i så fall funktionen r(t) är differentierbar i t.

Integral av en vektorfunktion

Vara r (t) = f (t) Yo + g (t) J + H (t) k en vektorfunktion, så att funktioner f, g och h är integrerbara i t.

Så:

$\dpi110 \int \mathbfr(t)dt =\left [ \int f(t)dt \right ]\mathbfi+\left [ \int g(t)dt \right ]\mathbfj+\left [ \int h(t)dt \right ]\mathbfk+\mathbfC$

Med:

C = c₁Yo + c₂J

Vilket innebär att integrationskonstanten också är en vektor, men konstant.

Exempel på vektorfunktion

Exempel 1

Du har vektorfunktionen som ges av r (t) = 3sec t Yo + 2tan t J. Det är möjligt att utvärdera det för olika t -värden, såsom t = π/4 och t = π, vilket ger upphov till vektorer r (π/4) och r (π):

r (π/4) = 3sec (π/4) Yo + 2tan (π/4) J = 3√2 Yo + 2 J

r (π) = 3sec (π) Yo+2tan (π) J = - 3 Yo

dock, r (t) Det finns inte för värden på t = ∓π/2, ∓3π/2, ∓5π/2 ... eftersom SEC -funktionen t = 1 /cos t Det är inte definierat, antingen är det så t = sen t / cos t.

Därför är domänen för R (T) -funktionen alla de verkliga värdena på T, utom de i formen:

∓ (2n+1) π/2; Med n = 0, 1, 2, .. .

Funktionens graf är en hyperbola:

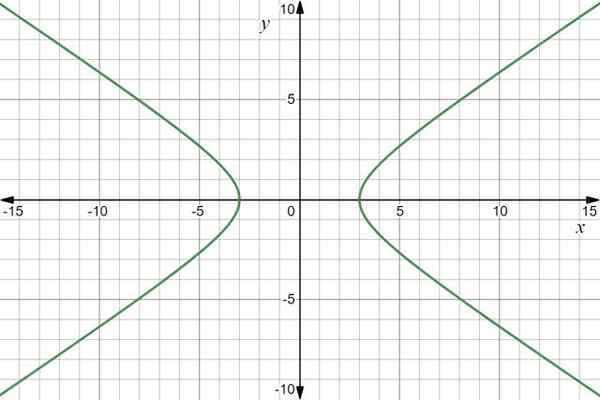Vektorfunktion graf r (t) = 3sec t Yo+2 tan t J. Källa: f. Zapata genom desmos.

Exempel 2

Vid den lutande projektillanseringen är den mobila positionen vektorfunktionen r (t) = x (t) Yo + och(t) J . Förutsatt att luftmotståndet inte ingriper, och att tyngdkraften är den enda kraften som verkar på mobilen, är den horisontella rörelsen enhetlig rektilinär, medan den vertikala är jämnt accelererad och är g = 9.8 m/s² Accelerationsvärdet. Denna acceleration är vertikal mot marken.

Kan tjäna dig: härledningsregler (med exempel)

I det här fallet är funktionerna X (t) och ((t) De är respektive:

x (t) = x_antingen + v_oxe∙ t
och (t) = y_antingen + v_Oy∙ T - ½ gt²

Beloppen v_oxe och v_Oy De är komponenterna i vektorfunktionen som beskriver den mobila hastigheten hela tiden:

v (t) = v_x(t) Yo + v_och(t) J

Med:

v_oxe = v_antingen∙ cos θ
v_Oy = v_antingen∙ Sen θ

Att vara θ den vinkel som bildar den initiala hastigheten med avseende på horisontellt.

För sin del är mobilens ursprungliga position koordinatpunkten (x_antingen,och_antingen) eller motsvarande positionsvektorn som ges av:

r_antingen (t) = x_antingen Yo + och_antingen J

Observera att i de visade ekvationerna har negativt tecken tilldelats den vertikala riktningen, så den tredje termen i ekvationen för y (t) tar det. Det är också möjligt att tilldela ursprungets ursprung till den ursprungliga positionen för mobilen.

Omedelbar projektilhastighet

Den omedelbara hastigheten V (t) är den första härledda från positionen med avseende på tid. Det beräknas genom att tillämpa de kända härledningsreglerna:

v(t) = R ' (t) = [x (t) Yo + och(t) J]'= x '(t) Yo + och'(t) J = v_oxeYo + (v_Oy - Gt) J

Hastighetsmodulen ges av:

$\dpi110 \left|\textbfv \right|=\sqrtv_ox^2+v_oy^2$

Omedelbar acceleration av projektilen

Det är känt att det är G, i vertikal riktning och riktning ner. Detta verifieras med att veta att acceleration är det första derivatet av hastighet med avseende på tid (eller det andra derivatet av positionen med avseende på tid, om det föredras):

till(t) = V ' (t) = [V_oxeYo + (v_Oy - Gt) J] '= [V_oxeYo] '+ [(v_Oy - Gt) J] '= = - g J

Detta är just det förväntade resultatet.

Träning löst

Med tanke på vektorfunktionen r (t) = 3t Yo + (T - 1) J, hitta R '(t) och r "(T).

Lösning

Tillämpa härledningsreglerna på var och en av komponenterna har du:

Kan tjäna dig: Integrationskonstant: Betydelse, beräkning och exempel

R '(t) = = 3 Yo + J

Och eftersom derivatet av en konstant är 0:

r "(t) = 0

Det vill säga, r "(t) är lika med nollvektorn.

Referenser

Figueroa, D. 2005. Serie: Physics for Science and Engineering. Volym 1. Kinematik. Redigerad av Douglas Figueroa (USB).
Larson, r. Beräkning med analytisk geometri. 2: a. Utgåva. McGraw Hill.
Matonlinje. Vektorvärderade funktioner. Återhämtat sig från: Mathonline.Wikidot.com.
Opentax. Kalkylvolym 3. Hämtad från: OpenStax.org.
Purcell, E. J. 2007. Beräkning. Pearson Education.