Matematik

Heptadecágono -egenskaper, diagonaler, omkrets, område

Heptadecágono -egenskaper, diagonaler, omkrets, område

han heptadecágono Det är en vanlig polygon på 17 sidor och 17 vertikaler. Dess konstruktion kan göras i den euklidiska stilen, det vill säga endast med regeln och kompassen. Det var matematikens stora geni Carl Friedrich Gauss (1777-1855) och räknade bara 18 års ålder, som hittade förfarandet för dess konstruktion 1796. 

Tydligen kände Gauss alltid mycket benägen att denna geometriska figur, till den punkten att han från den dag han upptäckte sin konstruktion beslutade att vara matematiker. Det sägs också att han ville att Heptadecágono skulle spelas in på hans gravsten.

Figur 1. Heptadecágono är en vanlig polygon på 17 sidor och 17 vertikaler. Källa: f. Zapata.

Gauss hittade också formeln för att avgöra vilka vanliga polygoner som har möjlighet att byggas med regel och kompass, eftersom vissa inte har exakt euklidisk konstruktion.

[TOC]

Egenskaper hos heptadecágono

När det gäller dess egenskaper, som varje polygon, är summan av dess inre vinklar viktig. I en vanlig polygon av n sidor, summan ges av:

Sa (n) = (n -2) *180º.

För heptadecágono n är 17, Vilket innebär att summan av dess inre vinklar är:

SA (17) = (17 - 2) * 180º = 15 * 180º = 2700º.

Denna summa, uttryckt i Radianes är så här:

Sa (17) = (17 - 2) * π = 15 * π = 15π

Från de föregående formlerna kan det enkelt härledas att varje inre vinkel på en heptadecágono har ett exakt α -mått som ges av:

α = 2700º/17 = (15/17) π -radianer

Det följer att den inre vinkeln ungefär är:

α ≈ 158 824º

Diagonaler och omkrets

Diagonal och omkrets är andra viktiga aspekter. I någon polygon är antalet diagonaler: 

D = n (n - 3) / 2 och i fallet med heptadecágono, till exempel N = 17, Du måste D = 119 diagonaler.

Kan tjäna dig: trinomial

Å andra sidan, om längden på varje sida av heptadecágono är känd, så lägger den vanliga heptadekonens omkrets helt enkelt 17 gånger den längden, eller vad som är motsvarande 17 gånger längden d På varje sida:

P = 17 d

Heptadecágono 

Ibland är bara radio känd r av heptadecágono, så det är nödvändigt att utveckla en formel för detta fall.

För detta ändamål konceptet apotem. Apotheme är det segment som går från mitten av den vanliga polygonen till mittpunkten på ena sidan. Apotemet relativt sidan är vinkelrätt mot den sidan (se figur 2).

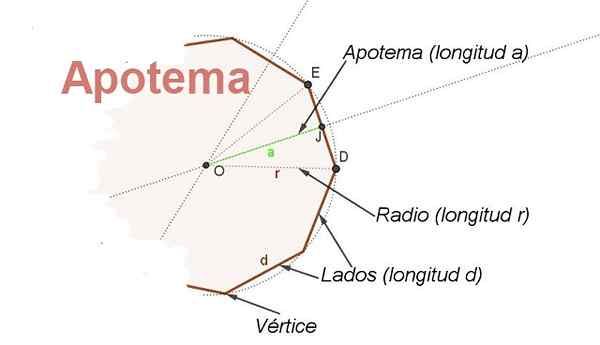figur 2. Delarna av en vanlig Radio R -polygon och dess apotem visas. (Egen utarbetande)

Dessutom är apotemet bisektor i vinkeln med centrala toppunkt och sidor på två på varandra följande vertikaler i polygonen, vilket gör det möjligt att hitta en relation mellan radioen r och sidan d.

Om det kallas p till den centrala vinkeln Hind Och med hänsyn till den apotemen Oj är bisector du har EX = D/2 = R SEN (β/2), där du har en relation att hitta längden d På sidan av en polygon känd sin radio r och dess centrala vinkel p:

D = 2 r sin (β/2)

När det gäller heptadecágon β = 360º/17 För vad du har:

D = 2 r sen (180º/17) ≈ 0,3675 r

Slutligen erhålls formeln för omkretsen av heptadecágono som känd dess radie:

P = 34 r sen (180º/17) ≈ 6.2475 r

Omkretsen av en heptadecágonon Pcir = 2π r ≈ 6.2832 r.

Område

För att bestämma området Heptadecágono kommer vi att hänvisa till figur 2, som visar sidorna och apotemet för en vanlig polygon av n sidor. I den figuren triangeln Eod Det har ett område som är lika med basen d (Polygonsida) efter höjd till (Polygon apothem) dividerat med 2:

Det kan tjäna dig: serie av kraft: exempel och övningar

Eod = (d x a) / 2

Så att kända apotem till av heptadecágono och sidan d av samma sak är:

Heptadecágono -område = (17/2) (d x a)

Område givet sidan

För att få en formel för Heptadecágono -området som vet längden på sina sjutton sidor är det nödvändigt att uppnå en relation mellan apotemlängden till och sidan d.

Med hänvisning till figur 2 har du följande trigonometriska relation:

Tan (β/ 2) = t.ex, varelse p till den centrala vinkeln Hind. Så att apotem till kan beräknas om längden är känd d från polygonsidan och den centrala vinkeln p:

A = (d/2) cotan (β/2)

Om detta uttryck för apotem ersätts nu, i formeln för Heptadecágono -området som erhållits i föregående avsnitt, har du:

Heptadecágono -område = (17/4) (D2) Cotan (β/2)

Varelse β = 360º/17 För heptadecágono, så du har äntligen den önskade formeln:

Heptadecágono -område = (17/4) (D2) Cotan (180º/17)

Området givet radion

I de föregående avsnitten hade ett förhållande mellan D -sidan av en vanlig polygon och dess R -radio hittats, följande varelse: Följande: Följande varelse:

D = 2 r sin (β/2)

Detta uttryck för d Det introduceras i uttrycket som erhållits i föregående avsnitt för området. Om de relevanta substitutionerna och förenklingarna görs erhålls formeln som gör det möjligt att beräkna Heptadecágono -området:

Heptadecágono -område = (17/2) (r2) Sin (β) = (17/2) (r2) SEN (360º/17)

Ett ungefärligt uttryck för området är:

Heptadecágono -området = 3 0706 (r2) 

Som förväntat är detta område lite mindre än området i cirkeln som omskriver Heptadecágon TILLCirkig = π r2 ≈ 3 1416 r2. För att vara exakt är den 2% lägre än den i dess omskrivna cirkel.

Kan tjäna dig: område med en vanlig och oregelbunden Pentagon: hur det tas, övningar

Exempel

Exempel 1

För att en heptadecágono ska ha 2 cm sidor, vilket värde bör radien och diametern för den omskrivna omkretsen ha? Hitta också omkretsvärdet.

För att svara på frågan är det nödvändigt att komma ihåg förhållandet mellan sidan och radien för en vanlig polygon av N -sidor:

 D = 2 r sen (180º / n)

För heptadecágono N = 17, därav D = 0,3675 r, Med andra ord

10 8844 cm i diameter.

Omkretsen av en 2 cm sida heptadecágon är p = 17* 2 cm = 34 cm.

Exempel 2

Hur mycket är området för en regelbunden heptadecágono de 2 cm sida?

Det är nödvändigt att hänvisa till den formel som visas i föregående avsnitt, som gör det möjligt att hitta området för en heptadecágono när längden är d På hans sida:

Heptadecágono -område = (17/4) (D2) / Solbränna (180º / 17) 

Vid ersättning D = 2 cm i den främre formeln erhålls:

Område = 90,94 cm

Referenser

  1. C. OCH. TILL. (2003). Geometrielement: med övningar och kompassgeometri. University of Medellin.
  2. Campos, f., Cerecedo, f. J. (2014). Matematik 2. Patria Redaktionsgrupp.
  3. Freed, K. (2007). Upptäck polygoner. Utbildningsföretag.
  4. Hendrik, V. (2013). Generaliserade polygoner. Birkhäuser.
  5. Iriger. (s.F.). Matematik första termin Tacaná. Iriger.
  6. Jr. Geometri. (2014). Polygoner. Lulu Press, Inc.
  7. Miller, Heeren och Hornsby. (2006). Matematik: Resonemang och applikationer (tionde upplagan). Pearson Education.
  8. Patiño, m. (2006). Matematik 5. Redaktionell progreso.
  9. Sada, m. Regelbundna 17 sidor med regel och kompass. Återhämtat sig från: Geogebra.org
  10. Wikipedia. Heptadecágono. Återhämtad från: är.Wikipedia.com