Hyperbel

Vad är en hyperbola?

Hyperbola är uppsättningen av punkter i planet så att det absoluta värdet på skillnaden mellan avståndet till två fasta punkter, kallade strålkastare, förblir konstant. Denna uppsättning punkter bildar kurvan med två grenar som observerats i figur 1.

Det finns en punkt P (x, y), FOCI f₁ och f₂ separerade ett avstånd lika med 2C. Det matematiska sättet att uttrycka detta förhållande är genom:

Figur 1. Hyperbola med horisontell fokalaxel. Källa: f. Zapata.

Alla punkter i hyperbola uppfyller detta tillstånd, vilket leder till hyperbola -ekvationen, som kommer att ses senare. Mittpunkten mellan strålkastarna kallas centrum C och i figuren sammanfaller den med punkten (0,0), men hyperbola kan också fördrivas och dess centrum motsvarar en annan koordinatpunkt C (H, K).

I den övre figuren är X -axeln fokalaxeln för hyperbola, eftersom det finns strålkastare, men du kan också bygga en vars fokalaxel är axeln och axeln.

Hyperbola är en del av de kurvor som kallas konisk, De kallas det eftersom de kan härledas från snittet av en kon med en platt sektion. En hyperbola erhålls vid korsning av konen och planet, förutsatt att den inte passerar genom konens toppunkt och vinkeln som bildar planet med konens axel är mindre än den som bildas med generatrix -axeln på konen samma.

Tillsammans med liknelsen, omkretsen och ellipsen är Conics kända sedan forntida tider. Den grekiska matematikern Apollonius från Perga (262-190 f.Kr.

Hyperbola egenskaper

Det här är några av de mest framstående egenskaperna hos en hyperbola:

1. Det är en platt kurva, därför räcker det att ge koordinaterna (x, y) för varje punkt som tillhör den.
2. Det är också en öppen kurva, till skillnad från omkretsen eller ellipsen.
3. Den har två grenar ordnade symmetriskt.
4. Både den vertikala axeln och den horisontella axeln kan betraktas som symmetriaxlar, men axeln där strålkastarna kallas fokalaxel eller huvudaxel.
5. Det är symmetriskt med avseende på dess centrum.
6. Hyperbola korsar fokalaxeln vid två punkter som kallas Häckar, Det är därför fokalaxeln ibland kallas riktig axel, Medan den andra axeln kallas Imagineraxel, Eftersom det inte har några punkter gemensamt med hyperbola.
7. Mitten av hyperbola ligger halvvägs mellan de punkter som kallas foci.
8. Det är associerat med två mycket speciella linjer som kallas asymptoter, som är linjer som hyperbola närmar sig, men utan att korsa dem, när värdena på x e y är mycket stora. Asymptoterna korsar varandra i mitten av hyperbolen.

Kan tjäna dig: överjektiv funktion: definition, egenskaper, exempel

Ekvationer och formler

Hiperbol -ekvation med mitt i (0,0)

Börjar från definitionen som gavs i början:

Till denna positiva konstant kallas det vanligtvis 2A och det är avståndet som skiljer hörn på hyperbola, då:

Å andra sidan, DP₁, Kardp₂ och 2c är sidorna på triangeln som visas i figur 1, och genom elementär geometri är subtraktionen av rutorna på sidorna på alla triangel alltid mindre än kvadratet för den återstående sidan. Så:

4th² < 4c²

OCH:

till < c

Detta resultat kommer att vara användbart inom kort.

Som avståndet mellan två punkter p₁(x₁,och₁) Och P₂(x₂,och₂) är:

Genom att ersätta koordinater P (x, y), f₁(-C, 0) och f₂(C, 0) Det kvarstår:

Vilket motsvarar:

Kvadrat i båda medlemmarna för att eliminera rötterna och omorganisera termerna du når:

Till kvantitet C² - till², vilket alltid är ett positivt belopp eftersom < c, se la denomina b², Därför skrivs ovanstående som:

b²x² - till²och² = a² b²

Dela alla termer av² b², Det är hyperbola -ekvationen centrerad på (0,0) med den horisontella riktiga axeln:

Med A och B större än 0. Denna ekvation kallas Hyerbola kanonisk ekvation och nämnaren till² Det motsvarar alltid den positiva fraktionen.

Hyperbola centrerad på (0,0) och med den verkliga axeln tar vertikal formen:

Korsningar av hyperbolen med koordinataxlarna

Korsningarna mellan hyperbola med koordinataxlarna görs respektive y = 0 och x = 0 i ekvationen:

För y = 0

x² /till² = 1 ⇒ x² = a²

x = ± a

Hyperbola skär till X -axeln i två punkter som kallas vertikaler, vars respektive koordinater x är: x = a y x = -a

För x = 0

Det erhålls -och² /b² = 1, som inte har någon verklig lösning och följer att hyperbola inte skärs till den vertikala axeln.

Hyperbola -ekvation med mitt i (H, K)

Om mitten av hyperbola är vid punkt C (H, K), är dess kanoniska ekvation:

Hiperbola element

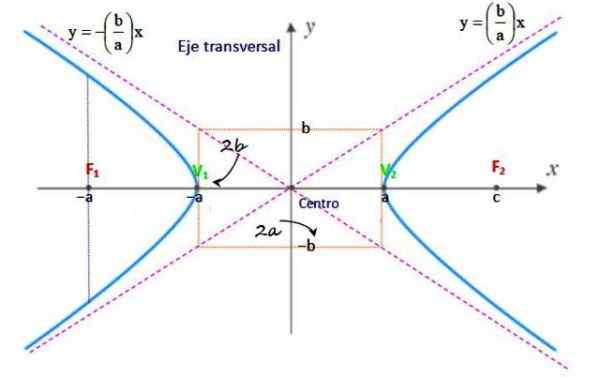figur 2. Hiperbola element. Källa: f. Zapata.

Centrum

Det är mittpunkten för segmentet f₁F₂ Och dess koordinater är (h, k) eller (x_antingen,och_antingen).

Kan tjäna dig: syntetisk uppdelning

Focos

De är de två fasta punkterna f₁ och f₂ som är på den verkliga axeln hos hyperbola, med avseende på vilken skillnaden mellan avstånd till punkt P (x, y) förblir konstant. Avståndet mellan strålkastarna och mitten av hyperbola är "C".

Vektorradio

Detta kallas avståndet mellan en punkt P och en av strålkastarna.

Brännvidd

Det är avståndet som skiljer båda strålkastarna och motsvarar 2C.

Häckar

Vertikalerna v₁ och v₂ De är de punkter där hyperbola korsar den riktiga axeln. Ett toppunkt och mitten av hyperbola separeras efter avstånd A, därför är avståndet mellan topparna 2A 2A.

Fokalaxel, huvudaxel eller riktig axel

Det är axeln där strålkastarna finns och mäter 2c. Det kan vara beläget på någon av de två kartesiska axlarna och hyperbola korsar den vid de punkter som kallas vertikaler.

Transversalaxel, sekundär axel eller imaginär axel

Det är axeln vinkelrätt mot fokalaxeln och mäter 2b. Hyperbola korsar det inte, så det kallas också en imaginär axel.

Asymptoter

De är två rader, vars respektive väntande är m₁ = (b/a) och m₂ = - (b/a), som är avsedda i mitten av hyperbola. Kurvan korsar aldrig dessa linjer och produkten mellan avståndet från någon punkt i hyperbola till asymptoterna, den är konstant.

För att hitta ekvationerna för asymptoterna, matchar bara vänster sida av hyperbola kanonisk ekvation till 0. Till exempel för hyperbola centrerad på ursprung:

Hyberbola rektangel

Det är rektangeln vars bredd är avståndet mellan topparna 2A och avstånd 2b och är fokuserad på mitten av hyperbola. Dess konstruktion underlättar den manuella layouten för hyperbola.

Rak sida

Rep som passerar genom en av strålkastarna, vinkelrätt mot den riktiga axeln.

Excentricitet

Det definieras som kvoten mellan fokalavståndet och den verkliga axeln:

E = c/a

Det är alltid större än 1, eftersom C är större än A och mindre än √2.

Värdet på och indikerar om hyperbola är ganska stängd (smal rektangel, långsträckt i riktning mot huvudaxeln) eller öppen (bred rektangel, långsträckt i riktning mot den imaginära axeln).

Rak tangent till hyperbola vid punkt P (x₁,och₁)

En tangentlinje till hyperbola vid en punkt P (x₁,och₁) Det är bisektorn för de två radiovektorerna i den punkten.

För en hyperbola med huvudaxeln parallellt med x -axeln tangentens lutning till hyperbola vid en punkt P (x₁,och₁) ges av:

Kan tjäna dig: kombinerade operationer

Och om hyperbola är huvudaxeln parallell med y -axeln, då:

Exempel på hyperbola

Spridning av alfapartiklar av en kärna

Genom att bombardera atomkärnor med alfakartiklar, som inte är något annat än heliumkärnor, avvisas dessa, eftersom någon atomkärna har en positiv laddning. Dessa heliumkärnor sprids efter hyperboliska banor.

Banor i solsystemets kroppar

Bild 3: Solsystemplaneter

I solsystemet rör sig föremål under tyngdkraften. Beskrivningen av rörelsen härrör från en differentiell ekvation där kraften är konservativ och omvänt proportionell mot avståndets kvadrat. Och lösningarna på denna ekvation är de möjliga banorna som följer föremålen.

Tja, dessa banor är alltid koniska: omkretsar, ellipser, liknelser eller hyperbolor. De två första är stängda kurvor, och det är så planeterna rör sig, men vissa kometer är fortfarande öppna banor, till exempel liknelser eller hyperbolor, med solen belägen i en av strålkastarna.

Lägsta ljud

När det finns två ljudkällor, till exempel två högtalare som avger låter jämnt i alla riktningar, belägna längs en rak linje, är minsta ljudintensitet (destruktiv störning) på en hyperbola vars huvudaxel sägs linje och i strålkastarna för Hyperbola är högtalarna.

Träning löst

Hitta elementen i följande hyperbola: vertikaler, foci och asymptoter av hyperbola och bygga dess graf:

Lösning

Mitten av denna hyperbola sammanfaller med koordinaternas ursprung och dess riktiga axel är horisontell, eftersom den positiva fraktionen motsvarar variabel x.

Hyperbola semi -axlarna är:

till² = 16 ⇒ a = 4

b² = 4 ⇒ B = 2

På detta sätt mäter den centrala rektangeln 4 enheter breda och 2 enheter höga. Kom ihåg att det nämndes ovan att c² - till² = B² , så:

c² = a² + b² ⇒ c² = 16 + 4 = 20

Därför är fokal semi-tjänst:

C = √20 = 2√5

Och fokuserna är på koordinatpunkter f₁ (-2√5.0) och f₂ (2√5.0).

Asymptoternas sluttningar är:

m = ± (b/a) = ± (2/4) = ± 0.5

Därför är respektive ekvationer för var och en:

och₁ = 0.5x; och₂ = -0.5x

Hyperbola kan enkelt grafera genom online -programvara som Geogebra:

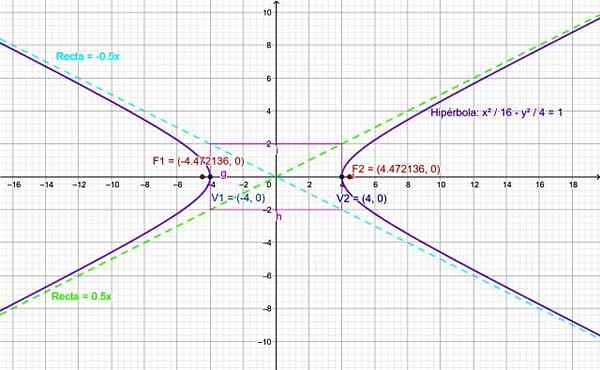Figur 4. Graf för övningen av övningen löst. Källa: f. Zapata.

Referenser

1. Fisisk. Hyperbola ekvation. Återhämtat sig från: Fisicalab.com
2. Hoffman, J. Urval av matematikfrågor. Volym 2.
3. Stewart, J. 2006. Preccculment: Matematik för beräkning. Femte. Utgåva. Cengage Learning.
4. Universumsformler. Hyperbolen. Återhämtat sig från: universalformulor.com
5. Zill, D. 1984. Algebra och trigonometri. McGraw Hill.