Matematisk jämlikhet
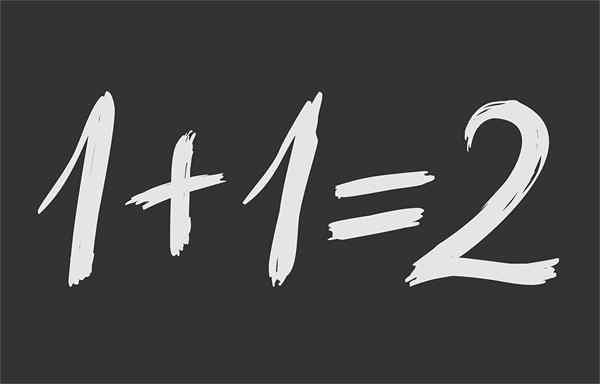
- 1607
- 473
- Johan Gustafsson
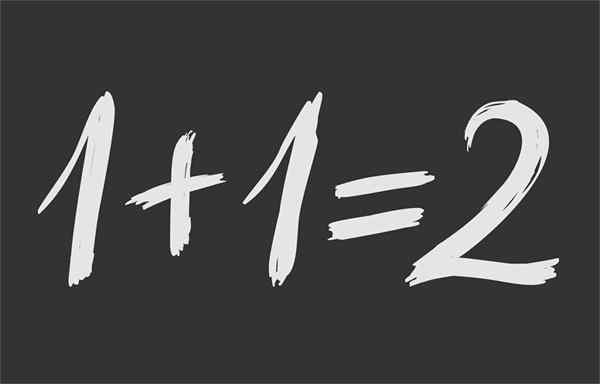 Figur 1.- Matematisk jämlikhet säkerställer att 1 + 1 är samma 2
Figur 1.- Matematisk jämlikhet säkerställer att 1 + 1 är samma 2 Vad är matematisk jämlikhet?
En matematisk jämlikhet säkerställer att två uttryck är desamma eller olika, de är helt likvärdiga. Dessa uttryck kan vara olika natur, till exempel nummer, bokstäver som symboliserar mängder eller storlekar, kombinationer av siffror och bokstäver, matriser och mer.
Symbolen som används för att beteckna jämlikhet på matematiskt språk är den för två parallella och horisontella linjer, som i tryckt text är den välkända symbolen "=". Om du till exempel har tre äpplen kan du skriva följande jämlikhet:
Antal äpplen = 3
Frasen "Antal äpplen" är medlem i vänster och nummer 3 är medlem till höger om jämlikhet.
Eftersom det är möjligt att skriva numeriska mängder på olika sätt används jämlikhet för att beteckna dem. Med ett specifikt fall för att illustrera poängen finns det flera sätt att skriva nummer 4, bortsett från det mest uppenbara som är 4 = 4, kan följande skrivas, genom en matematisk jämlikhet:
2 + 2 = 4
6 - 2 = 4
8 ÷ 2 = 4
2 × 2 = 4
22 = 4
Den jämlikhet som visas här är sant, men en jämlikhet kanske inte är till exempel 10 + 5 = 20 är falsk, eftersom 10 + 5 = 15.
Visst vet läsaren andra sätt att skriva nummer 4. Observera att uttryck på varje sida av jämlikhet kan vara siffror, ord, bokstäver som symboliserar mängder eller andra symboler, till exempel:
x + 1 = 7
till2B - 1 = xy
f (x) = 2x2
Matematiker använde inte alltid jämställdhetssymbolen, så de gamla matematikfördragen var mycket omfattande.
Det tillskrivs matematikern och doktor Robert minns (1510-1558), född i Wales, skapandet av jämställdhetssymbolen "=", så bekant för alla idag. Kom ihåg, tydligen trött på att skriva hela tiden frasen "precis som" i ett av hans matematikfördrag, bestämde han sig för att förkorta i sin plats släktingarna parallella ränder.
Kan tjäna dig: Pentagonal Prism: Egenskaper, delar, vertikaler, kanter, volymEgenskaper för matematisk jämlikhet
Följande egenskaper tillåter att arbeta korrekt med matematisk jämlikhet. De är axiomatiska, så de kräver inte demonstration:
1.- Reflekterande egendom
Den här egenskapen konstaterar att alla belopp är lika med sig själv. I synnerhet, eftersom valfritt antal är lika med sig själv, kan lika stora skrivas:
5 = 5
36.35 = 36.35
Om ett belopp är bokstavligt, eller det är en kombination av bokstäver och siffror, är det också lika med sig själv:
3x = 3x
till2före Kristus-1 = a2före Kristus-1
2.- Symmetriegenskap
Mängderna eller medlemmarna på båda sidor av jämlikhet kan bytas ut utan förlorad giltighet. Det vill säga, om det som är till vänster om "=" -symbolen är skriven till höger, och vad som är till höger placeras till vänster, är det samma jämlikhet.
Exempelvis är uttryck 5 + 2 = 7 motsvarande den här: 7 = 5 + 2. På samma sätt:
12 + 8 = 20; 20 = 12 + 8
x + 1 = 3; 3 = x + 1
x - z = y; y = x - z
3.- Transitiv egendom
Den här egenskapen hänvisar till jämlikhetens likvärdighet. Om två jämlikhet har en gemensam medlem är de också desamma, eftersom i allmänhet:
Om "x = y" och "y = z" då x = z
För att illustrera den här egenskapen, överväg dessa två numeriska jämlikheter: 2 + 2 = 4 och 6 - 2 = 4. Eftersom båda är lika med 4 (de har en gemensam medlem), kan följande skrivas utan att förlora någon giltighet:
2 + 2 = 6 - 2
Ett annat exempel, den här gången med brev:
Ja x + 1 = 5
OCH
A - B = 5
Så:
x+1 = a - b
4.- Avbokningsegenskap
En jämlikhet ändras inte om det i båda medlemmarna finns samma belopp som lägger till (eller subtraherar) och det beslutas att eliminera eller avbryta detta. Detta är summan avbokningsegenskap.
Ta som exempel följande numeriska jämlikhet där de 10 visas både i medlemmen i höger och i den till vänster:
Det kan tjäna dig: trigonometriska funktioner: grundläggande, i det kartesiska planet, exempel, träning2 + 2 + 10 = 6 - 2 + 10
Nummer 10 kan avbrytas utan att jämlikhet tappar sin giltighet, vilket lämnar en annan kortare jämlikhet och motsvarande den föregående:
2 + 2 = 6 - 2
I jämlikhet (10 ÷ 2) - 3 = 5 - 3 Heltalet - 3 tillhör både jämställdhetsmedlemmar och visas som att lägga till, kan därför avbrytas, erhålla:
10 ÷ 2 = 5
Det händer också med bokstavliga mängder, till exempel:
Ja x + 2y + z = −a + b + z
Då kan "Z" avbrytas, eftersom det finns på båda sidor av jämlikhet som att lägga till (och med samma tecken).
På så sätt resulterar det:
x + 2y = −a + b
Det kan också definiera avbokningsegenskapen för multiplikation. Om samma belopp C multiplicerar båda jämställdhetsmedlemmarna kan detta belopp avbrytas, till exempel:
Cx = cy
Då kan C avbrytas för att få helt enkelt:
x = y
5.- Enhetlighetsegenskap
En jämlikhet förblir oundviklig genom att lägga till, subtrahera, multiplicera eller dela med samma mängd på båda sidor av samma.
Till exempel måste det till 8 + 5 = 13, om båda medlemmarna multipliceras med visst godtyckligt nummer C = 2 kvarstår jämlikhet:
(8+5) × 2 = 13 × 2
13 × 2 = 26
Matematiska lika klasser
Det finns olika typer av matematisk jämlikhet, så de klassificeras för sin bästa förståelse i:
-Identitet, De är jämlikhet där båda medlemmarna är identiska:
2 = 2
x = x
2x = x + x
och så vidare.
-Ekvationer, Detta är jämlikheter där en eller flera okända visas och är sanna för vissa värden, det vill säga jämlikhet inte uppfylls för något godtyckligt värde, så de är också kända som villkorade jämställdhet. Exempel:
x + 1 = 5
x3 = 27
A + B = 40
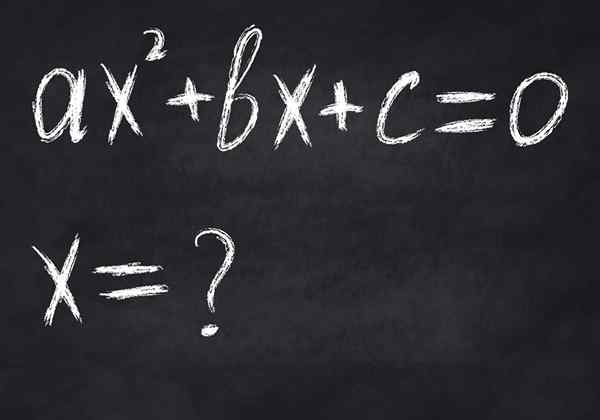 figur 2.- En ekvation är en villkorad matematisk jämlikhet, eftersom den bara uppfylls för vissa variabla värden. Bilden visar en andra gradsekvation, som högst har två riktiga lösningar
figur 2.- En ekvation är en villkorad matematisk jämlikhet, eftersom den bara uppfylls för vissa variabla värden. Bilden visar en andra gradsekvation, som högst har två riktiga lösningar -Likvärdighet, I dem är medlemmen i vänster motsvarande den till höger, även om de inte är lika, till exempel i: 23 = 8.
Kan tjäna dig: tillsatsprincip-Formler, Det är en jämlikhet som alltid uppfylls för värdena på den oberoende variabeln, som i den välkända formeln för avståndet D beroende på tid t för en mobil med enhetlig rätlinjig rörelse: D = v ∙ t
Löst övningar
Övning 1
Skriv nummer 10 till fyra olika och motsvarande jämlikhet.
Lösning
Alla dessa jämlikheter uttrycker nummer 10, men på olika sätt:
5 × 2 = 10
11-1 = 10
101= 10
20 ÷ 2 = 10
Övning 2
Vad är värdet på x som uppfyller jämlikhet x + 1 = 3?
Lösning
Denna jämlikhet är en ekvation, eftersom värdet på X är okänt. Med hjälp av egenskap 5, om uttrycket x + 1 = 3 tillsätts (−1) på båda sidor av symbolen "=", återstår jämlikhet:
x + 1 + (−1) = 3 + ( - 1)
När man lägger till (−1) till vänstermedlemmen och operationen är löst, är "x" ensam på vänster sida av jämlikhet, denna procedur kallas undanröjning:
x + 1 - 1 = 3−1
x = 2
Därför är värdet som tillfredsställer denna jämlikhet x = 2.
Övning 3
Om en mobil med enhetlig rätlinjig rörelse har en hastighet på 2.5 m/s, vad är avståndet som går efter 3 sekunder?
Lösning
Formeln som ses i föregående avsnitt används, D = v ∙ t, där värdet på V ersätts:
D = 2.5 ∙ T
Uttrycket blir en jämlikhet när t = 3 sekunder och operationen löses:
D = 2.5 ∙ 3 m = 7.5 m
Vilket resulterar i jämlikhet:
D = 7.5 m
Referenser
- Barnett, r. 2000. Förskulptur. 4th. Utgåva. McGraw Hill.
- Larson, r. 2012. Förskulptur. 8th. Utgåva. Cengage Learning.
- Pérez, v. Algebraisk jämlikhet. Återhämtat sig från: matematik.Laguia2000.com.
- Jämlikhetsegenskaper. Hämtad från: PPS.K12.Eller.oss.
- Stewart, J. 2007. Förberäkning: Matematik för beräkning. Femte. Utgåva. Cengage Learning.

