Magnetiska induktionsformler, hur det beräknas och exempel

De magnetinduktion eller magnetisk flödesdensitet är en förändring av miljön orsakad av närvaron av elektriska strömmar. De modifierar arten av det omgivande rymden och skapar en fält Vektor.

Vektorn Magnetisk induktion, magnetisk flödesdensitet Eller bara magnetiskt fält B, Den har tre distinkta egenskaper: en intensitet uttryckt av ett numeriskt värde, en adress och också en känsla som ges vid varje punkt i rymden. Det är markerat med fetstil för att skilja det från rent numeriska mängder eller skalar.

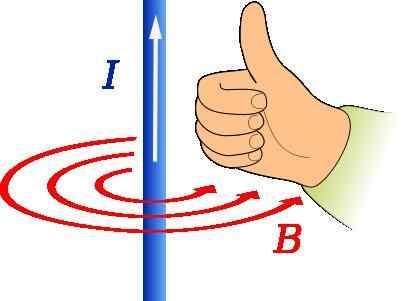Höger tumregel för att bestämma riktningen och riktningen för den magnetiska induktionsvektorn. Källa: JFMelero [CC BY-SA 4.0 (https: // CreativeCommons.Org/licenser/BY-SA/4.0)]

Den högra tumregeln används för att hitta riktningen och riktningen för magnetfältet härstammat av en tråd som transporterar ström, som visas i figuren ovan.

Tummen på höger hand bör peka i strömmen. Då indikerar de återstående fingrarna formen av B, att i figuren representeras av de koncentriska cirklarna av rött.

I detta fall adressen till B Det är tangentiellt för den koncentriska omkretsen med tråden och betydelsen strider mot klockhänderna.

De magnetinduktion B I det internationella systemet mäts Tesla (T), men det är vanligare att mäta den i en annan enhet som heter Gauss (G). Båda enheterna utnämndes respektive till hedern för Nikola Tesla (1856-1943) och Carl Friedrich Gauss (1777-1855) för deras extraordinära bidrag till vetenskapen om el och magnetism.

[TOC]

Vilka är egenskaperna för magnetisk induktion eller magnetisk flödesdensitet?

En kompass som placeras nära tråden med strömmen, kommer alltid att i linje med B. Den danska fysikern Hans Christian Oersted (1777-1851) var den första som insåg detta fenomen i början av 1800-talet.

Kan tjäna dig: areolär hastighet: hur det beräknas och lösta övningar

Och när strömmen upphör pekar kompassen på det geografiska norr, som alltid. Genom att noggrant ändra kompassens position erhålls en karta från magnetfältformen.

Denna karta har alltid formen av koncentriska cirklar till tråden, som beskrivs i början. På detta sätt kan det visualiseras B.

Även om tråden inte är rak, vektorn B kommer att bilda koncentriska cirklar runt den. För att bestämma vilken form fältet har räcker det att föreställa sig mycket små trådsegment, så små att de verkar rätlinjiga och omgiven av koncentriska omkretsar.

Magnetfältlinjer producerade av en trådslinga som transporterar ström. Källa: Pixabay.com

Detta indikerar en viktig egenskap hos magnetfältlinjerna B: De saknar princip eller slut, de är alltid stängda kurvor.

Biot-Savart-lagen

Det nittonde århundradet bestämde början på era av elektricitet och magnetism i vetenskapen. Nära år 1820 Franska fysiker Jean Marie Biot (1774-1862) och Felix Savart (1791-1841) upptäckte lagen som bär hans namn och som tillåter beräkning av vektorn B.

De gjorde följande observationer om bidraget till magnetfältet som produceras av ett differentiallängd trådsegment dl som transporterar en elektrisk ström Yo:

• Storleken på B minskar med det omvända till kvadratet på avståndet till tråden (detta är vettigt: långt ifrån tråden intensiteten av B Det måste vara mindre än i närliggande punkter).
• Storleken på B Det är proportionellt mot strömmen Yo som reser på tråden.
• Adressen till B Det är tangentiellt för radioomkretsen r centrerad på tråd och riktningen för B Det ges, som sagt, av den högra tumregeln.

Vektor eller produktskorsprodukt är lämpligt matematiskt verktyg för att uttrycka den sista punkten. För att upprätta en vektorprodukt behövs två vektorer, som definieras enligt följande:

• dl Det är vektorn vars storlek är längden på det differentiella segmentet dl
• r Det är vektorn som går från tråden till den punkt där du vill hitta fältet

Kan tjäna dig: elektromagnetiskt spektrum: egenskaper, band, applikationer

Formler

Allt detta kan kombineras i ett matematiskt uttryck:

Proportionalitetskonstanten som är nödvändig för att fastställa jämlikhet är Magnetisk permeabilitet för ledigt utrymme μ_antingen  = 4π.10^-7 T.m/a

Detta uttryck är Biot och Savarts lag, som gör att du kan beräkna magnetfältet för ett aktuellt segment.

Sådant segment måste i sin tur vara en del av en större och större krets: en aktuell distribution.

Villkoret för att kretsen är stängd är nödvändigt för att en elektrisk ström ska flyta. Elektrisk ström kan inte flyta i öppna kretsar.

Slutligen, för att hitta det totala magnetfältet för denna nuvarande distribution, läggs alla bidrag för varje differentialsegment till dl. Detta motsvarar att integrera all distribution:

För att tillämpa biot-savart-lagen och beräkna den magnetiska induktionsvektorn är det nödvändigt att överväga mycket viktiga viktiga punkter:

• Vektorprodukten mellan två vektorer resulterar alltid i en annan vektor.
• Storleken på vektorprodukten i biot-savart-lagen är:var θ är vinkeln mellan dl och r.
• Vektorprodukten ska hittas innan Om den integrerade upplösningen är löst, löses integralen av var och en av de komponenter som erhålls separat.
• Det är nödvändigt att dra situationen och etablera ett adekvat koordinatsystem.
• När förekomsten av någon symmetri observeras måste den användas för att spara beräkningstid.
• När det finns trianglar är Pythagoras Theorem och Cosine Theorem till stor hjälp för att fastställa det geometriska förhållandet mellan variablerna.

Hur beräknas det?

Med ett praktiskt exempel på beräkningen av B För rätlinjig tråd tillämpas dessa rekommendationer.

Det kan tjäna dig: punktlig belastning: egenskaper och coulomb -lag

Exempel

Beräkna den magnetfältvektorn som en mycket lång rätlinjig tråd producerar vid en punkt P i utrymmet, enligt den visas som visas.

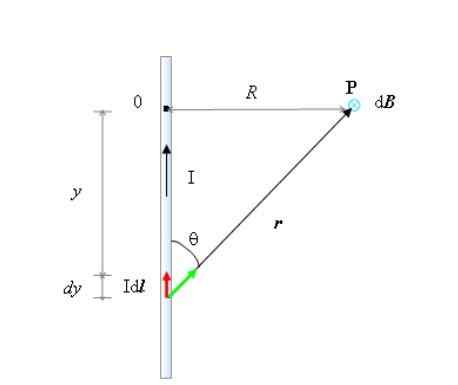
Geometri som är nödvändig för att beräkna magnetfältet vid punkt P, av en oändligt lång strömtråd. Källa: Självgjord.

Från figuren måste du:

• Tråden riktas vertikalt, med den ström jag flödar upp. Denna adress är +och i koordinatsystemet, vars ursprung är vid punkt eller.
• θ är vinkeln mellan dl och r Och det är också sant att: 
• I det här fallet, enligt rätt tumregel, B Vid punkt P är riktad i papperet, så det betecknas med en liten cirkel och en "X" i figuren. Denna adress kommer att tas som -z.
• Den högra triangeln vars ben är och och R, relaterar båda variablerna enligt Pythagoras teorem: r²= R²+och²

Allt detta ersätts i det integrerade. Vektorn eller tvärprodukten indikeras av dess storlek plus riktning och dess betydelse:

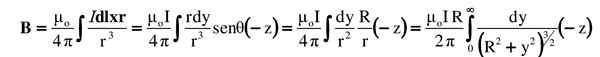
Den föreslagna integralen söks i en integrerad tabell eller löses av en lämplig trigonometrisk substitution (läsaren kan kontrollera resultatet med hjälp av y = rtg θ):

Resultatet överensstämmer med det förväntade: fältets storlek minskar med avståndet R och ökar proportionellt med intensiteten hos den nuvarande I.

Medan en oändligt lång tråd är en idealisering, är uttrycket erhållet ett mycket bra tillvägagångssätt för området för en lång tråd.

Med biot- och Savart -lagen är det möjligt att hitta magnetfältet för andra höga symmetrifördelningar, till exempel en cirkulär spiral som transporterar ström eller vikta ledningar som kombinerar rätlinjiga och krökta segment.

För att analysera den integrerade måste naturligtvis ha en hög grad av symmetri. Annars är alternativet numeriskt att lösa det integrerade.

Referenser

1. Serway, R., Jewett, J. (2008). Fysik för vetenskap och teknik. Volym 2. Mexiko. Cengage Learning Editors. 367-372.