Ömsesidig induktansformel/koefficient, applikationer, övningar

De ömsesidig induktans beskriver interaktionen mellan två kommande 1 och 2 spolar, genom vilken en variabel ström Yo Cirkulerande genom spole 1, producerar ett förändrat magnetfältflöde som korsar spole 2.

Detta flöde är proportionellt mot strömmen och proportionalitetens konstant är ömsesidig induktans₁₂. Vara φ_B2 Magnetfältet flöde genom spole 2, då kan du skriva:

Φ_B2 = M₁₂ Yo₁

Figur 1.- Transformatorn är den huvudsakliga tillämpningen av ömsesidig induktans. Källa: Pixnio.

Och om spolen 2 har n₂ Varv:

N₂ . Φ_B2 = M₁₂ Yo₁

På detta sätt₁₂ Mellan båda spolarna är:

M₁₂ = N₂ . Φ_B2 / Yo₁

Ömsesidig induktans har Weber/Amperio eller WB/A -enheter, som kallas Henry eller Henrio och förkortat h. Därför motsvarar 1 Henry 1 WB/ A.

Värdet på m₁₂ Det beror på geometrien mellan spolarna, deras form, deras storlek, antalet varv på varje och det avstånd som skiljer dem, liksom den relativa positionen mellan dem.

[TOC]

Ömsesidiga induktansapplikationer

Fenomenet med ömsesidig induktans har många tillämpningar tack vare det faktum att dess ursprung är i Faraday-Lenz-lagen, som säger att variabla strömmar i en krets inducerar strömmar och spänningar i en annan, utan behov av kretsar att anslutas med kablar av kablar.

När två kretsar interagerar på detta sätt sägs det att de är magnetiskt kopplade. På detta sätt kan energi gå från en till en annan, en omständighet som kan användas på flera sätt, vilket demonstreras av Nikola Tesla i början av 1900 -talet (se träning Löst 1).

I sina ansträngningar för att överföra el utan kablar upplevde Tesla med olika enheter. Tack vare dess upptäckter skapades transformatorn, enheten som rör sig från el från växterna till hem och industrier.

Kan tjäna dig: enhetsvektorer: egenskaper, hur man får ut det, exempel

Transformatorn

Transformatorn överför mycket höga alternativa spänningar i de elektriska linjerna, vilket minimerar värmeförluster och levererar samtidigt maximal energi till konsumenterna.

När spänningen når måste dessa minskas, vilket uppnås med transformatorn. Detta består av två trådspolar rullade runt en järnkärna. En av spolarna med n₁ Vändningar är anslutna till en alternativ spänning och kallas primär. Den andra, som är sekundär, har n₂ Vänds, ansluter till ett motstånd.

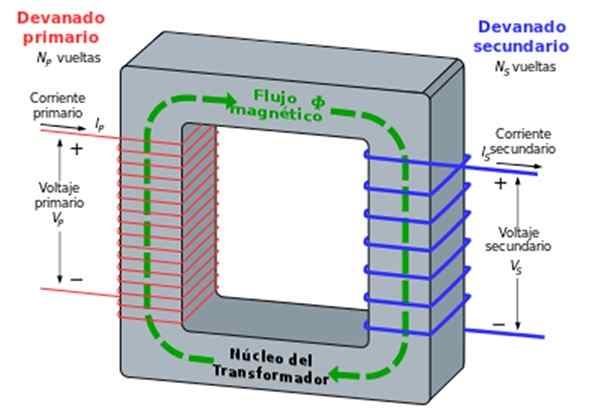figur 2. Transformatorn. Källa: Wikimedia Commons.

Järnkärnan säkerställer att alla magnetfältlinjer som passerar genom en spole också gör det för den andra.

Faradays lag konstaterar att orsaken mellan V -spänningarna₂ /V₁ (sekundär /primär) är lika med orsaken mellan antalet varv n₂ /N₁:

V₂ /V₁ = N₂ /N₁

Justera korrekt antalet varv, en spänning större eller mindre än ingången erhålls vid utgången.

Transformatorerna är byggda av många storlekar, från enorma transformatorer i elektriska installationer till mobiltelefonlastare, bärbara datorer, MP3 och andra elektroniska enheter.

Pacemaker

Effekterna av ömsesidig induktans finns också i pacemaker för att upprätthålla frekvensen av hjärtslag, så att det kan hålla blodflödet stabilt.

Pacemaker arbetar med batterier. När de är utmattade kan en yttre spole överföra kraft till en annan spole inuti pacemakern. Eftersom proceduren utförs genom induktion är det inte nödvändigt att skicka patienten till en ny intervention när batteriet är uttömt.

Det kan tjäna dig: kalibreringskurva: vad är det för, hur man gör det, exempel

Trådlösa lastare

Medan en annan vanlig applikation är trådlösa lastare för olika föremål som tandborstar och mobiltelefoner, som är enheter med låg elförbrukning.

I framtiden höjs användningen av trådlösa lastare för elbilbatterier. Och många forskning idag syftar till att producera trådlös el i hem. En av de viktigaste begränsningarna för ögonblicken är avståndet vid vilket strömmarna kan induceras tack vare magnetfälten.

Löst övningar

- Övning 1

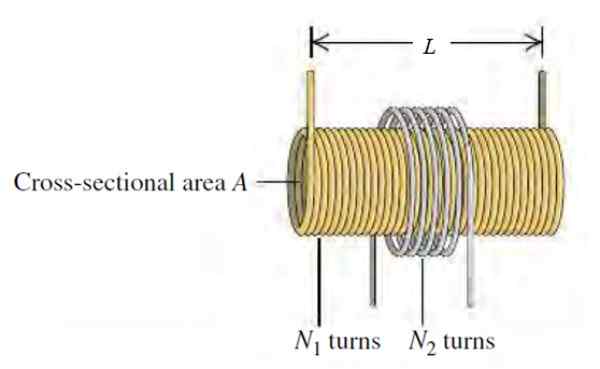
I en version av Tesla -spolen, som används som högspänningsgenerator i vissa laboratoriedemonstrationer, finns det en lång längd L, Radio R, Radio R, Radio R, Radio R, Radio R, Radio R, Radio R₁ med n₁ rund per enhetslängd, koaxiellt omgiven av en cirkulär radiobin r₂ och n₂ rund.

Figur 3. En Tesla -spole. Källa: Sears Zemansky. Universitetsfysik.

a) Hitta den ömsesidiga induktans m i kretsen, beror det på strömmen som cirkulerar genom magnetventilen?

b) beror ömsesidig induktans på spolens form eller om dina svängar är mer eller mindre rullade ihop?

Lösning till

Magnetfältets magnetfält är proportionell mot antalet varv och strömmen som cirkulerar genom det, vilket betecknas som jag₁, Eftersom magnetventilen är krets 1. Det ges av uttrycket:

B₁ = μ_antingenN₁.Yo₁ / L

Det magnetiska fältflödet som magnetventilen skapar i en spiral av spolen, som är krets 2, är produkten av fältets intensitet av området kopplat till fältet:

Φ_B2 = B₁. TILL₁

Vart man ska₁ Det är området för tvärsnittet av magnetventilen och inte av spolen, eftersom magnetfältet är ogiltigt utanför det:

Det kan tjäna dig: lysande kroppar: egenskaper och hur de genererar sitt eget ljus

TILL₁ = π (r₁)²

Vi ersätter området i ekvationen för φ_B2:

Φ_B2 = B₁. π (r₁)² = (μ_antingenN₁.Yo₁ / L). π (r₁)²

Och ömsesidig induktans ges av:

M₁₂ = N₂ . Φ_B2 / Yo₁ = N₂. [(μ_antingenN₁.Yo₁ / L). π (r₁)² ] / Yo₁

M₁₂ = μ_antingen N₁ N₂ . π (r₁)² / L

Det beror inte på strömmen som cirkulerar genom magnetventilen, som vi såg att den är avbruten.

Lösning B

Som vi ser beror den ömsesidiga induktansen inte på spolens form, inte heller när strumporna dras åt. Spolens enda inflytande i ömsesidig induktans är antalet varv som finns i den, vilket är n₂.

- Övning 2

Två spolar är mycket nära varandra och en av dem genomför en variabel ström under den tid som ges av följande ekvation:

I (t) = 5.00 E ^{-0.0250 T} Sen (377 t) a

Vid t = 0.800 sekunder Den inducerade spänningen i den andra spolen mäts och erhåller -3.20 v. Hitta den ömsesidiga induktansen hos spolarna.

Lösning

Vi använder ekvationen:

ε₂ = - m₁₂ (gav₁/dt)

Till ömsesidig induktans bland spolarna kallar vi det helt enkelt m, eftersom vanligtvis m₁₂ = M_tjugoett. Vi kommer att behöva det första derivatet av strömmen med avseende på tid:

gav av₁/dt =

= - 0.0250 x 5.00 E ^{-0.0250 T} x sin (377 t) - 377 cos (377 t) x 5.00 E ^{-0.0250 T}  Ess

Vi utvärderar detta derivat i t = 0.800 s:

gav av₁/dt = - 0.0250 x 5.00 E ^{-0.0250 x 0.800} x sin (377 x 0.800) - 377 cos (377 x 0.800) x 5.00 E ^{-0.0250 x 0.800}  A/s =

= -5.00 E ^{-0.0250 x 0.800} [0.0250 X SEN (377 x 0.800) + 377 cos (377 x 0.800)] =

= -1847.63 a/s

M = -3.20 V / -1847.63 a/s = 0.001732 h = 1.73 MH.

Referenser

1. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Volym 6. Elektromagnetism. Redigerad av Douglas Figueroa (USB).
2. Hewitt, Paul. 2012. Konceptuell fysisk vetenskap. Femte. Ed. Pearson.
3. Riddare, r.  2017. Fysik för forskare och teknik: En strategistrategi. Pearson.
4. Sears, f. (2009). University Physics Vol. 2.
5. Serway, R., Jewett, J. (2008). Fysik för vetenskap och teknik. Volym 2. 7th. Ed. Cengage Learning.