Destruktiv formel och ekvationer, exempel, träning, träning

De förstörande inblandning, I fysiken inträffar det när två oberoende vågor som kombineras i samma rymdregion är föråldrade. Sedan möter åsna på en av vågorna dalarna i den andra och resultatet är en våg med en nollamplitud.

Flera vågor passerar utan problem genom samma punkt i rymden och sedan följer var och en sin väg utan att påverkas, till exempel vågorna i vattnet i följande figur:

Figur 1. Regndroppar producerar vågor på vattenytan. När de resulterande vågorna har nollbredd sägs det att störningar är förstörande. Källa: Pixabay.

Anta att två vågor av lika amplitud till och frekvens Ω, som vi kommer att kalla och₁ och och₂, som kan beskrivas matematiskt genom ekvationer:

och₁= En sen (kx -Ω)

och₂ = En SEN (kx -ωt + φ)

Den andra vågen och₂ Den har ett gap φ med avseende på den första. När de kombineras, eftersom vågor kan överlagras utan problem, ger de upphov till en resulterande våg som kallas och_R:

och_R = y₁ + och₂ = En sen (kx -Ω) + en synd (kx -Ωt + φ)

Genom trigonometrisk identitet:

Sin α + sin β = 2 sin (α + ß)/2 . cos (α - β)/2

Ekvationen för och_R Det förvandlas in:

och_R = [2a cos (φ/2)] sin (kx - ωt + φ/2)

Nu har denna nya våg en resulterande amplitud till_R = 2a cos (φ/2), som beror på fasskillnaden. När denna fasskillnad förvärvar värdena+π eller -π är den resulterande amplituden:

TILL_R = 2a cos (± π/2) = 0

Eftersom cos (± π/2) = 0. Precis är då när destruktiv störning mellan vågor inträffar. I allmänhet, om kosinus argument är av formen ± kπ/2 med udda k, amplituden till_R  Det är 0.

[TOC]

Destruktiva interferensexempel

Som vi har sett, när två eller flera vågor passerar samtidigt genom en punkt, överlappar de, vilket ger upphov till en resulterande våg vars amplitud beror på fasskillnaden mellan deltagarna.

Kan tjäna dig: linjär variation: koncept, exempel, träning löst

Den resulterande vågen har samma frekvens och vågnummer som de ursprungliga vågorna. I följande animation överlagras två vågor i blå och gröna färger. Den resulterande vågen är i rött.

Amplituden växer när störningen är konstruktiv, men den avbryts när den är förstörande.

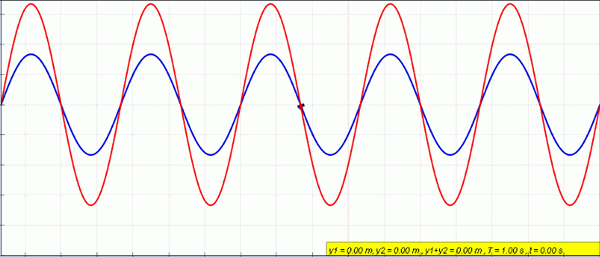figur 2. Blå och grönfärgade vågor överlappar varandra för att ge upphov till den röda vågen. Källa: Wikimedia Commons.

Vågorna som har samma amplitud och frekvens kallas sammanhängande vågor, Så länge de håller mellan dem samma fasskillnad φ. Ett sammanhängande vågexempel är laserljus.

Villkor för destruktiv inblandning

När de blå och gröna vågorna är föråldrade 180 º vid en given punkt (se figur 2), betyder det att medan de rör sig, de har fasskillnader φ av π -radianer, 3π radianer, 5π radianer och så vidare.

På detta sätt, genom att dela argumentet om den resulterande amplituden med 2, resulterar det (π/2) radianer, (3π/2) radianer ... och kosinus för sådana vinklar är alltid 0. Därför är störningen förstörande och amplituden görs 0.

Destruktiv vågstörning i vatten

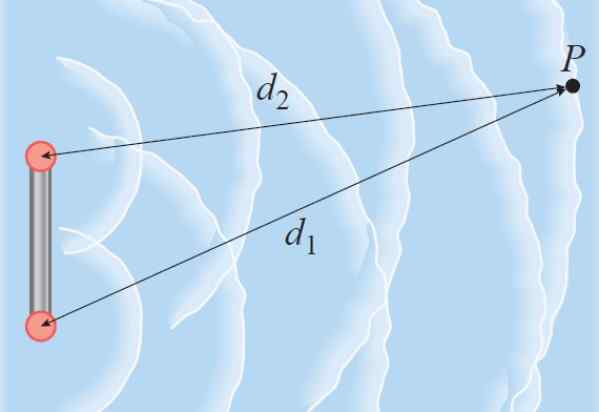
Anta att två sammanhängande vågor börjar i en med varandra. Sådana vågor kan vara de som sprider sig genom vattnet tack vare två staplar som vibrerar. Om de två vågorna reser till samma punkt P, turnerar olika avstånd, är fasskillnaden proportionell mot banskillnaden.

Figur 3. Vågorna som produceras av de två källorna reser i vattnet till punkten P. Källa: Giambattista, a. Fysik.

Som en våglängd λ är lika med en skillnad på 2π -radianer, då är det sant att:

│D₁ - d₂│ / λ = fasskillnad / 2π radianer

Fasskillnad = 2π x│d₁ - d₂│/ λ

Kan tjäna dig: polarisering av ljus: typer, exempel, applikationer

Om vägarnas väg är ett udda antal våghalvågor, det vill säga: λ/2, 3λ/2, 5λ/2 och så vidare, är störningen förstörande.

Men om vägskillnaden är ett vridmomentantal våglängder är störningen konstruktiv och amplituderna läggs till vid punkt P.

Destruktiv störning av lysande vågor

Ljusvågor kan också störa varandra, som framställts av Thomas Young 1801 genom deras berömda dubbla slitsexperiment.

Young gav ljus genom en slits tillverkad på en ogenomskinlig skärm, som enligt Huygens -principen, i sin tur genererar två sekundära ljuskällor. Dessa källor fortsatte på väg igenom en andra ogenomskinlig skärm med två slitsar och det resulterande ljuset projicerades på en vägg.

Diagrammet observeras i följande bild:

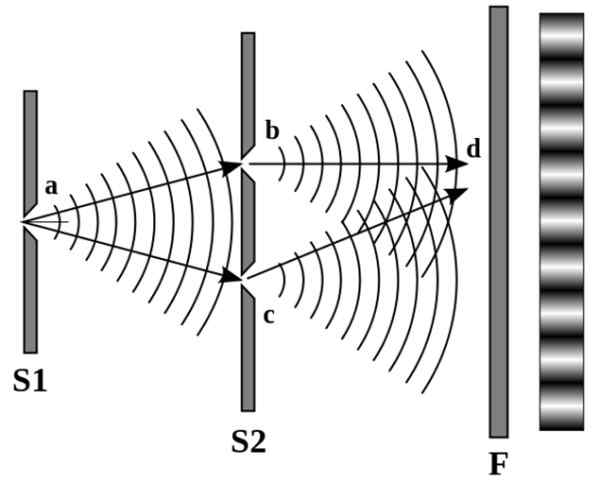Figur 4. Mönstret av ljusa och mörka linjer på höger vägg beror på konstruktiv respektive destruktiv störning. Källa: Wikimedia Commons.

Young observerade ett distinkt mönster av alternativa ljus och mörka linjer. När ljuskällor stör störande är linjerna mörka, men om de gör konstruktivt är linjerna tydliga.

Ett annat intressant interferensexempel är tvålbubblor. Det här är mycket tunna filmer, där störningen inträffar eftersom ljuset reflekteras och bryts på ytorna som begränsar tvålfilmen, både över och under.

Figur 5. På en tunn tvålfilm bildas ett interferensmönster. Källa: PXFuel.

Som filmens tjock. Resultatet är ett mönster av färger om infallsljuset är vitt.

Det beror på att det vita ljuset inte är monokromatiskt, men det innehåller alla våglängder (frekvenser) av det synliga spektrumet. Och varje våglängd ser ut som en annan färg.

Det kan tjäna dig: lysande kroppar: egenskaper och hur de genererar sitt eget ljus

Träning löst

Två identiska högtalare som drivs av samma oscillator är separerade 3 meter och en lyssnare är 6 meter från mittpunkten för separationen mellan högtalarna, vid punkt eller.

Flytta sedan till punkt P, på ett vinkelrätt avstånd på 0.350 i punkten eller, som visas i figuren. Där slutar lyssna på ljudet för första gången. Vad är våglängden där oscillatorn avger?

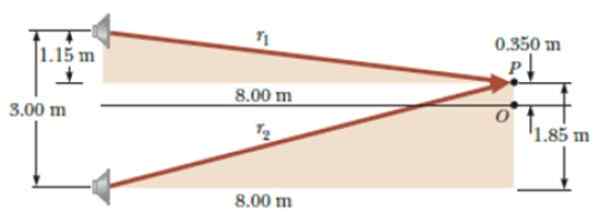Figur 6. Diagram för övningen löst. Källa: Serway, R. Fysik för vetenskap och teknik.

Lösning

Amplituden hos den resulterande vågen är 0, därför är störningen förstörande. Du måste:

Fasskillnad = 2π x│r₁ - r₂│/ λ

Av Pythagoras teorem som appliceras på figurens skuggade trianglar:

r₁ = √1.femton² + 8² M = 8.08 m; r₂ = √1.85² + 8² M = 8.21 m

│R₁ - r₂│ = │8.08- 8.21 │ M = 0.13 m

Minsta förekommer i λ/2, 3λ/2, 5λ/2 ... den första motsvarar λ/2, då, formeln för fasskillnaden är:

λ = 2π x│r₁ - r₂│/ fasskillnad

Men fasskillnaden mellan vågorna måste vara π, så att amplituden till_R = 2a cos (φ/2) vara null, då:

λ = 2π x│r₁ - r₂│/ π = 2 x 0.13 m = 0.26 m

Referenser

1. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Volym 7. Vågor och kvantfysik. Redigerad av Douglas Figueroa (USB).
2. Fisisk. Vågstörning. Återhämtat sig från: Fisicalab.com.
3. Giambattista, a. 2010. Fysik. 2: a. Ed. McGraw Hill.
4. Serway, R. Fysik för vetenskap och teknik. Volym 1. 7th. Ed. Cengage Learning.
5. Wikipedia. Sömnplåt störning. Källa: Det är.Wikipedia.org.