Divergerande linsegenskaper, element, typer, applikationer

De divergerande linser är de som är tunnare i dess centrala och tjockare del vid kanterna. Som en konsekvens separerar de (divergera) de ljusstrålar som påverkar dem parallellt med huvudaxeln. Deras tillägg slutar konvergera i fokusbilden till vänster om linsen.

Divergent eller negativa linser som de är kända bildar vad som kallas virtuella bilder av objekt. De har olika applikationer. I synnerhet används de i oftamologi för att korrigera myopi och vissa typer av astigmatism.

Randrijo87 [CC BY-SA 4.0 (https: // CreativeCommons.Org/licenser/BY-SA/4.0)]

Så om du lider av myopi och bär glasögon har du ett perfekt exempel på divergerande lins.

[TOC]

Egenskaper hos divergerande linser

Som förklarats ovan är de divergerande linserna smalare i sin centrala del än vid kanterna. Dessutom är en av dess ytor i denna typ av linser alltid konkav. Detta ger denna typ av linser en serie egenskaper.

Till att börja med resulterar förlängningen av strålarna som påverkar dem i virtuella bilder som inte kan samlas in på någon typ av skärm. Detta är så, eftersom strålarna som korsar linsen inte konvergerar någon gång, eftersom de avviker i alla riktningar. Beroende på linsens krökning öppnas dessutom i större eller mindre utsträckning.

En annan viktig egenskap hos denna typ av linser är att fokus är till vänster om linsen, så att det är mellan detta och objektet.

Dessutom är bilderna i olika linser mindre än objektet och är mellan detta och fokus.

Jipaul / från Henrik [CC BY-SA 3.0 (https: // CreativeCommons.Org/licenser/BY-SA/3.0)]

Delar av divergerande linser

När du studerar dem är det viktigt att veta vilka element som utgör linserna i allmänhet och de divergerande linserna i synnerhet.

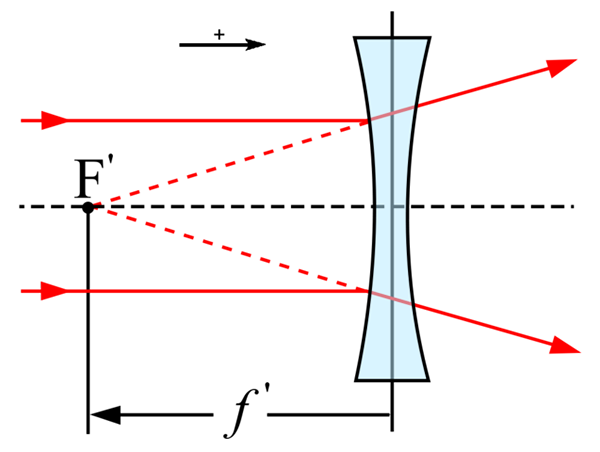
Det kallas det optiska centrumet för en lins till den punkt genom vilken strålarna inte upplever någon avvikelse. Huvudaxeln är å andra sidan den linje som ansluter sig till den punkten och huvudfokuset, den senare representeras med bokstaven F.

Kan tjäna dig: spänningskälla

Huvudfokuset får den punkt där alla strålar som påverkar linsen parallellt med huvudaxeln finns.

På detta sätt kallas avståndet mellan det optiska centrumet och fokuset fokalavstånd.

Krökningscentra definieras som centrumen för sfärerna som skapar linsen; på detta sätt är krökningsradioerna radionerna på sfärerna som ger upphov till linsen. Och slutligen kallas linsens centrala plan.

Bildbildning

För att grafera bildandet av en bild i en tunn lins är det bara nödvändigt att veta riktningen som två av de tre strålarna kommer att följa
vars bana är känd.

En av dem är den som påverkar linsen parallellt med linsens optiska axel. Detta, när den bryts ut i linsen, kommer att gå igenom fokusbilden. Den andra av strålarna vars bana är känd är den som korsar det optiska centrumet. Detta kommer inte att se dess bana modifierad.

Den tredje och sista är den som passerar genom objektfokuset (eller dess förlängning korsar objektfokuset) som efter brytning kommer att följa en riktning parallellt med den för linsens optiska axel.

På detta sätt kommer i allmänhet att bildas en eller annan typ av bild i linserna beroende på objektets eller kroppens position med avseende på linsen.

Men i det speciella fallet med divergerande linser, oavsett kroppens position framför linsen, kommer bilden som kommer att bildas att ha vissa egenskaper. Och i divergerande linser kommer bilden alltid att vara virtuell, mindre än kroppen och höger.

Kan tjäna dig: flödesnummer: hur det beräknas och exempel

Ansökningar

Det faktum att de kan separera ljuset som korsar dem ger divergerande linser några intressanta egenskaper inom optikområdet. På detta sätt kan de korrigera myopi och vissa specifika typer av astigmatism.

De divergerande oftalmiska linserna separerar ljusstrålarna så att när de når det mänskliga ögat är de mer distanserade. Således, när de går igenom hornhinnan och linsen går de längre och kan nå näthinnan som kör synproblemen för de människor som lider av myopi.

Grabbar

Som vi redan har nämnt har konvergerande linser minst en konkav yta. På grund av detta finns det tre typer av divergerande linser: bicócavas, planocóvas och konvexo-cócavas.

Bicócavas divergerande linser består av två konkava ytor, planknaderna har en konkav och en plan yta, medan i den konvexa divergerande menisken en yta är en yta är något konvex och den andra är konkav.

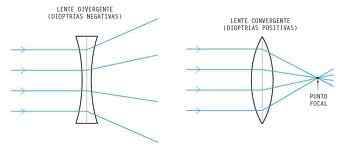
Skillnader med konvergerande linser

I konvergerande linser, i motsats till vad som händer i divergerande, minskar tjockleken från mitten till kanterna. I denna typ av lins är således ljusstrålarna som påverkar huvudaxeln parallellt koncentrerade eller konvergerar vid den enda punkten (i fokus). På detta sätt skapar de alltid riktiga bilder av objekt.

I optik används konvergerande eller positiva linser främst för att korrigera långsynthet, presbyopia och vissa typer av astigmatism.

Grantexgator [CC BY-SA 3.0 (https: // CreativeCommons.Org/licenser/BY-SA/3.0)]

Gauss -ekvation av linserna och ökad lins

Den typ av lins som studeras vanligtvis kallas tunna linser. Således definieras alla linser vars tjocklek är mycket liten jämfört med krökningsradioerna för ytorna som begränsar dem.

Studien av denna typ av linser kan huvudsakligen genomföras genom två ekvationer: Gauss -ekvationen och ekvationen som gör det möjligt att bestämma ökningen i linsen.

Gauss -ekvation

Betydelsen av Gauss -ekvationen av de tunna linserna ligger i det stora antalet grundläggande optiska problem som gör det möjligt att lösa. Ditt uttryck är som följer:

Kan tjäna dig: elliptiska galaxer: bildning, egenskaper, typer, exempel

1/f = 1/p +1/q

Där 1/ f är linsen och f är fokalavståndet eller avståndet från det optiska centret till focam. Måttenheten på en linsens kraft är diopter (d), är värdet av 1 d = 1 m^-1. Å andra sidan är P och Q respektive avståndet vid vilket ett objekt och det avstånd till vilket dess bild observeras.

Träning löst

En kropp placeras 40 centimeter från en divergerande lins på -40 centimeter fokalavstånd. Beräkna bildens höjd om objektets höjd är 5 cm. Bestäm också om bilden är rätt eller inverterad.

Vi har följande data: h = 5 cm; P = 40 cm; F = -40 cm.

Dessa värden ersätts i Gauss -ekvationen för de tunna linserna:

1/f = 1/p +1/q

Och det erhålls:

1/-40 = 1/40 +1/Q

Där q = - 20 cm

Därefter ersätter vi resultatet som tidigare erhållits i ekvationen för ökningen i en lins:

M = - Q / P = - -20 / 40 = 0,5

Att få att värdet på ökningen är:

M = h '/h = 0,5

Rensa denna ekvation h ', som är värdet på bildens höjd, det når:

H '= H/2 = 2,5 cm.

Bildhöjden är 2.5 cm. Dessutom är bilden rätt eftersom M> 0 och minskade eftersom det absoluta värdet på M är mindre än 1.

Referenser

1. Ljus (n.d.). I Wikipedia. Hämtad den 11 april 2019 från detta.Wikipedia.org.
2. Lekner, John (1987). Reflektionsteori, av elektromagnetiska och delvågor. Kandare.
3. Ljus (n.d.). I Wikipedia. Hämtad den 11 april 2019 från.Wikipedia.org.
4. Lins (n.d.). I Wikipedia. Hämtad den 11 april 2019 från detta.Wikipedia.org.
5. Lins (optik). I Wikipedia. Hämtad den 11 april 2019 från.Wikipedia.org.
6. Acts, Eugene (2002). Optik (4: e upplagan.). Addison Wesley.
7. Tupler, Paul Allen (1994). Fysisk. 3: e upplagan. Barcelona: Jag vände.