Biot-Savart lagformel, demonstration, applikationer, övningar

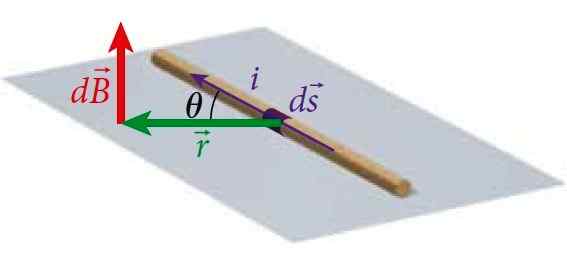
De Biot-savart Upprättar en relation mellan magnetfältet DB  vid en punkt P, producerad av en tunn tråd som transporterar en ström i och vars differentiella längd är ds. Denna lag används för att hitta magnetfältet för nuvarande fördelningar genom Superpositionsprincip. 

Detta innebär att för att beräkna det totala magnetfältet vid punkt P måste vi lägga till alla bidrag som varje differentiell del Ds av tråden bidrar. Och denna summa görs genom en integrerad genomförd över hela nuvarande distribution.

Figur 1. Ett trådsegment transporterar en ström I, som producerar ett magnetfält vid en punkt P på ett visst avstånd från tråden, som beräknas av Biot-Savart-lagen. Källa: Bauer, W. Fysik för teknik och vetenskap.

På detta sätt kan du beräkna fältet som producerar ledningar med aktuella geometrier.

Biot-Savarts lag är uppkallad efter de två franska fysiker som upptäckte den 1820: Jean Marie Biot (1774-1862) och Felix Savart (1791-1841). För att uppnå detta var de tvungna att studera intensiteten och formen på magnetfältet som produceras av många strömfördelningar.

[TOC]

Formel

Det matematiska uttrycket för biot-savart-lagen är som följer:

Det upprätthåller analogier med motsvarande att beräkna det elektriska fältet: Coulombs lag, bara att magnetfältet DB i P är vinkelrät till planet där tråden är belägen. Vi kan se detta i figur 1.

Det tidigare uttrycket kan också skrivas enligt följande:

I båda uttryck, r Det är positionsvektorn, riktad från ID -aktuella elementets till den punkt där du vill beräkna fältet.

Kan tjäna dig: bevarande av den linjära momentum: princip, exempel, övningar.

För sin del, r Med en circumflejo -accent är det den enhetliga vektorn som riktas i samma riktning och riktning, men med en modul lika med 1. Vektorn r Det representeras enligt följande:

Av denna anledning, genom att ersätta i den tidigare ekvationen -den som har r³ I nämnaren- uttrycket r nås omedelbart² I nämnaren.

Förutom de ovannämnda vektorerna innehåller formeln den ständiga μ_antingen, ring upp Vakuumpermeabilitet och vars värde är:

μ_antingen = 4π x10^-7 T.m/ a.

Om vi ​​vill beräkna magnetfältvektorn är det nödvändigt att integrera all den aktuella distributionen, för vilka vi behöver uppgifterna om dess geometri:

Vektorprodukten och den högra regeln

Biot-Savart-lagen involverar en vektorprodukt mellan ID-vektorers och r. Resultatet av en vektorprodukt mellan två vektorer är också en vektor.

I detta fall ID Vector -produktmodulens x r IS: (ids) ⋅r⋅senθ, där θ är vinkeln mellan ids och r, som visas i figur 1.

På detta sätt är fältets storlekB Det ges av:

Riktningen och betydelsen kan bestämmas med regeln för höger hand, som illustreras i denna figur:

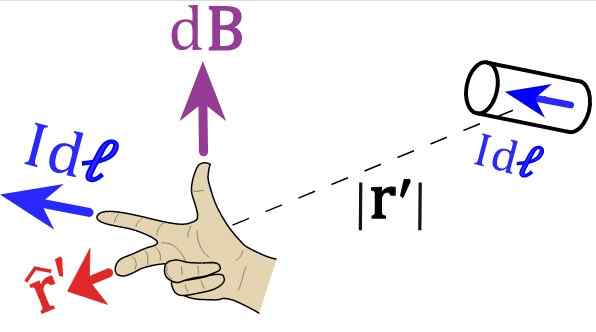figur 2. Högerhandregel för biot-savartlag. Källa: Wikimedia Commons.

Vi inbjuder läsaren att placera sin högra hand efter vektorerna i figurerna 1 och 2. För figur 1 måste pekfingret peka till vänster efter IDs eller idl, Malfingfingret pekar enligt vektorn r enhetlig.

Och slutligen riktas tummen upp och detta är magnetfältets riktning.

Kan tjäna dig: ellipsoid: egenskaper och exempel

Demonstration av biot-savart-lagen

Biot-Savart-lagen är mycket experimentell, vilket innebär att dess formulering kommer från många observationer om beteendet hos magnetfältet som produceras av nuvarande ledningar.

Biot- och Savart -observationer

Dessa var observationerna från franska forskare om magnetfältet DB:

-Storleken på DB är omvänt proportionell mot r².

-Det är också direkt proportionellt mot storleken på det aktuella elementet, som kallas IDs Och även till sen θ, där θ är vinkeln mellan vektorerna ds och r.

-dB är vinkelrätt mot båda ids -Riktningen för strömmen r.

-Olika av dB är tangentiellt för en radiocirkel r trådcentrerad. Med andra ord, fält B producerat av ett aktuellt segment består av koncentriska omkretsar till de karga.

-Betydelsen som den kretsar B Det ges av den högra tumregeln: den högra tummen pekas i riktningen för strömmen och de återstående fyra fingrarna är krullade runt tråden efter cirkulationen av fältet.

Alla dessa observationer kombineras i det matematiska uttrycket av den tidigare beskrivna lagen.

Biot-Savart Law Applications

När den nuvarande distributionen har hög symmetri kan integral enkelt lösas, låt oss se några fall:

Rätlinjig och tunn tråd

En rätlinjig tråd av längd L transporterar en ström i, till exempel den som visas i figuren.

Det illustrerar den nödvändiga geometrien för beräkningen av fältet. Detta är vinkelrätt mot pappersarket, utgående till planet om strömmen flyter från vänster till höger och på annat sätt (kontrollera det med högerhandregeln).

Kan tjäna dig: paramagnetism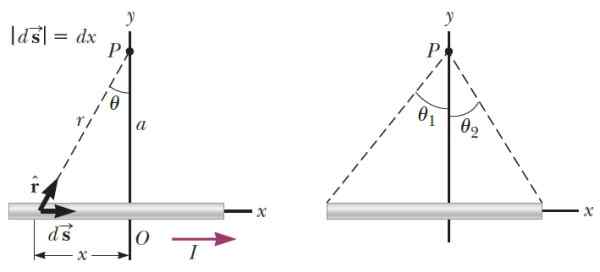Figur 3.- Till vänster den geometri som krävs för att beräkna magnetfältet som producerar ett tunt trådsegment vid punkt P. Till höger kan vinklarna som bestämmer P -positionen med avseende på segmentets ändar. Källa: Serway, R. Fysik för vetenskap och teknik.

Vara k  Enhetsvektorn i riktningen vinkelrätt mot planet, efter att ha genomfört processen att integrera, är magnetfältet som tråden producerar i P:

Cirkulära spira

Den radiocirkulära slingan till Den transporterar en ström som visas i figuren och producerar ett magnetfält DB -i mörkgrön- vid punkt P på den axiella axeln, på avstånd x från mitten.

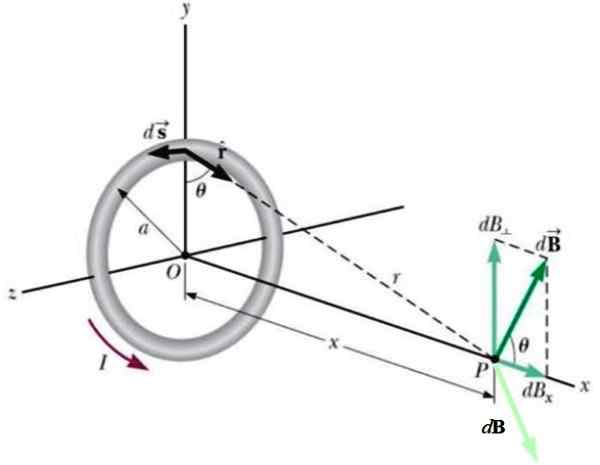Figur 4.- Geometri för beräkning av fältet som produceras av cirkulärspasen vid punkt P på den axiella axeln. Källa: Wikimedia Commons.

Ett annat aktuellt element som ligger på motsatt sida skulle ge ytterligare ett bidrag till DB (ljusgrönt), så att dess vertikala komponent avbryts med den första.

Resultatet är att nätmagnetfältet är horisontellt, så det är bara integrerat i dessa komponenter, vilket resulterar i:

Träning löst

Det finns en extremt lång tråd som transporterar en ström på 2 till flödet som visas på bilden. Beräkna magnetfältets storlek på ett radiellt avstånd på 5 cm från tråden.

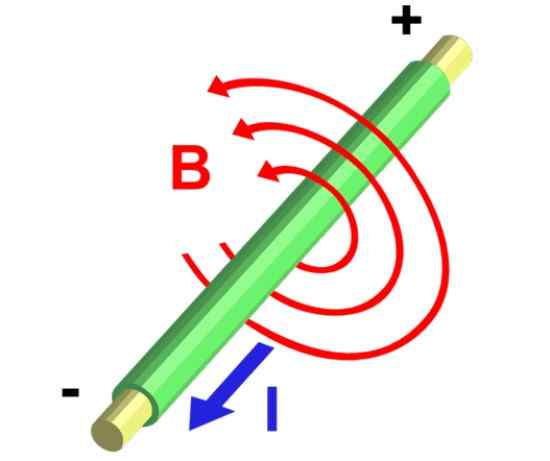Figur 5.- Magnetfältlinjer i ett rätlinjigt trådsegment som transporterar ström. Källa: Wikimedia Commons.

Lösning

Eftersom det är en mycket lång tråd kan vi ta uttrycket för det rätlinjiga segmentet och göra θ₁= 0º och θ₂ = 180º för gränsvinklar. Detta räcker för att trådens längd ska lagra oändlighet.

På detta sätt kommer vi att ha fältet är:

Det förenklar:

Nu ersätter vi värdena på uttalandet:

I = 2 a

R = 5 x10^-2 m

μ_antingen= 4π x10^-7 T.m/ a

Riktningen och känslan av B De visas i figur 5, där riktningen som lämnar arket har tagits som k.

Referenser

1. Bauer, w. 2011. Fysik för teknik och vetenskap. Volym 1. MC Graw Hill.
2. Figueroa, D. 2005. Serie: Physics for Science and Engineering. Volym 6. Elektromagnetism. Redigerad av Douglas Figueroa (USB).
3. Giancoli, D.  2006. Fysik: Principer med applikationer. Sjätte. Ed Prentice Hall.
4. Resnick, r. 1999. Fysisk. Vul. 1. 3: e upplagan. på spanska. Kontinentala redaktionella företag s.TILL. av C.V.
5. Sears, Zemansky. 2016. Universitetsfysik med modern fysik. 14th. Ed. Volym 1.
6. Serway, R., Jewett, J. 2008. Fysik för vetenskap och teknik. Volym 2. 7th. Ed. Cengage Learning.