Kemi

Lag i flera proportioner

Lag i flera proportioner

Vad är lagen i flera proportioner?

De Lag i flera proportioner Den konstaterar att om två element bildar mer än en förening när de reagerar på varandra, så är andelen massor som en av dem kombineras med en fast massa av den andra, det är lika med ett förhållande mellan små antal.

Lagens uttalande kan verka komplicerat om du inte har ett exempel till hands. Tänk därför på några oreos -kakor, bestående av två chokladlock och en remsa av sockerkräm: T2C (t = lock och c = grädde). Om vi ​​ville uppfinna en mer robust Oreo -kakan, skulle vi lägga till en annan remsa av grädde för att få dubbel grädde (T2C2 eller tc).

I desserter, som Oreos -kakor, har vi proportioner som kan varieras helt enkelt för att förbereda andra versioner av dem. Källa: Brokensphere, CC BY-SA 3.0 https: // CreativeCommons.Org/licenser/BY-SA/3.0 via Wikimedia Commons

Vi kan också lägga till en annan, så att kakan har tre gånger mer grädde än en konventionell cookie (T2C3). Vad händer om vi lägger ett annat chokladlock i mitten av de vita ränderna (T3C2)? Alternativen är obegränsade; Men vi lägger alltid till ett lock eller en krämenhet. Vi tänker inte på ett halvt av locket (1/2 t) eller en femtedel av grädden (1/5 C), eftersom det skulle vara olämpligt.

På samma sätt som det händer med de kemiska elementen: deras atomer delar inte för att bilda föreningar. Därför "massorna av t eller c bland deras föreningar" alltid "en enkel relation.

Förklaring

Proportioner

Lagen om flera proportioner, tillsammans med lagen om de definierade proportionerna, föregick stökiometri och de första kemiska formlerna. Låt oss glömma kakorna, men låt oss behålla sina symboler: T och C. Genom experiment upptäcks att element t och c bildar flera föreningar: t2C, tc och t2C3.

Innan de kemiska formlerna var det omöjligt att veta på en gång som var proportionerna av massorna av T och C i sådana föreningar. Var tvungen att bestämma dem först. I en förening upptäcktes att massan av T fördubblades till den för C; För att säga, 2 gram T kombineras med 1 gram c.

Kan tjäna dig: kapacitans: enheter, formler, beräkning, exempel

Sedan, i den andra föreningen, måste massorna av T och C matchas: 2 gram T kombineras nu med 2 gram C. Här uppstår frågan: vad händer om T och C fortfarande kan bilda en annan förening? Om så är fallet, skulle det säkert bildas med 2 gram T, men den här gången skulle de kombineras med 3 gram C (1 gram + 1 gram + 1 gram).

Enkla massförhållanden

Proportionerna av massorna som T och C reagerar tillåter att fastställa sina kemiska formler: T2C (2 gram t: 1 gram c), TC (2 gram t: 2 gram c) och t2C3 (2 gram t: 3 gram c). Om vi ​​vill jämföra förhållandena mellan T- eller C -massorna i dessa föreningar, är det nödvändigt att en av dess massor förblir konstant; I detta fall är det av t: 2 gram.

Därför kommer vi att bestämma andelen massa av C i dessa tre föreningar:

  • T2C: 1 gram c/2 gram t
  • TC: 2 gram c/2 gram t
  • T2C3: 3 gram c/2 gram t

Vi kommer att ha en relation för massan av C lika med 1: 2: 3. Det vill säga det finns två gånger mer C i TC än i T2C och 3 gånger mer c i t2C3 än i T2C. Som man kan se är 1: 2: 3 små heltal (de överstiger inte ens dussin).

Exempel på lagen i flera proportioner

För följande exempel kommer samma tidigare steg att tillämpas, men vi kommer att ta hänsyn till de molära massorna av respektive element, förutsatt att en mol av föreningen.

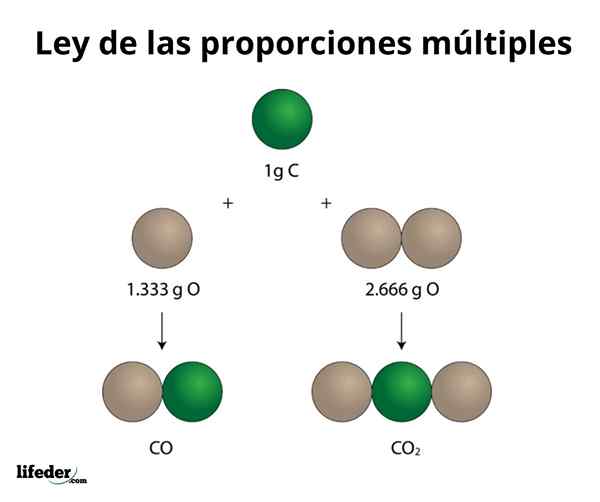
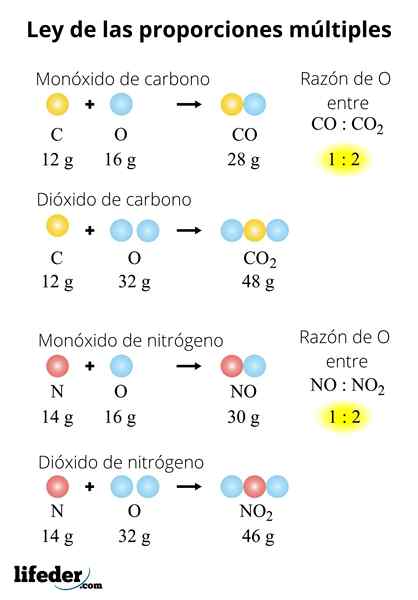
KOKOS2

Detta exempel förklarar på ett enkelt sätt hur lagen i flera proportioner fungerar; I CO (kolmonoxid) finns det 1.333 gram syre för varje gram kol. I koldioxid (CO₂) finns det 2.666 gram syre för varje gram kol. Därför är andelen syre i båda föreningarna 1: 2, ett litet heltalsnummer.

H2ÅH2ANTINGEN2

De flera proportioner lagen gäller för paret av h2ÅH2ANTINGEN2.

Kan tjäna dig: 30 exempel på kemiska suspensioner

I en mol av h2Eller, 2 gram väte kombineras med 16 gram syre. Under tiden i en mol av h2ANTINGEN2, 2 gram väte kombineras med 32 gram syre. För att verifiera om denna lag är uppfylld måste vi ställa in samma massa för ett av elementen i båda föreningarna. Den här gången är väte: 2 gram.

Massproportioner för h2Eller och h2ANTINGEN2 är:

  • H2O: 16 gram eller/2 gram h
  • H2ANTINGEN2: 32 gram eller/2 gram h

Förhållandet mellan massan av O kommer att vara 16:32. Vi kan dock förenkla det genom att dela med 16 och stanna 1: 2. Återigen består det slutliga förhållandet av små hela siffror.

Sw2-Sw3

I en mol av så2, 32 gram svavel kombineras med 32 gram syre. Under tiden, i en mol av så3, 32 gram svavel kombineras med 48 gram syre. Svavelmassan är densamma för båda föreningarna, så vi kan direkt jämföra syreproportioner:

  • Sw2: 32 gram eller
  • Sw3: 48 gram eller

Att vara förhållandet mellan syremassan mellan båda föreningarna lika med 32:48 eller 1: 1.5. Men var inte där att det borde finnas hela siffror? Förhållande 1: 1.5 (1/1.5) Det kan också skrivas som 2: 3 (0.6), och återigen kommer vi att ha små hela siffror: 2 och 3.

Observera att vi också kunde ha skrivit förhållandet som 48:32 eller 1.5: 1, är resultatet 3: 2. Lagen förändras inte, bara tolkningen av förhållandet: det finns 1.5 eller 3/2 gånger mer syre i SO3 det i så2; vilket är detsamma att säga att det finns 2/3 eller 0.6 gånger mindre syre i SO2 det i så3.

NEJ NEJ2-N2PÅ2ANTINGEN3-N2ANTINGEN5

Lagen kan också tillämpas för en serie föreningar. Tänk på kväveoxider: inte-inte2-N2PÅ2ANTINGEN3-N2ANTINGEN5. För att utvärdera denna lag i dem måste vi ställa in en massa kväve: 28 gram. Därför att? För nej och nej2 De har en kväveatom mindre än de andra oxiderna:

  • 2 (nr): 28 gram n/32 gram eller
  • 2 (Nej2): 28 gram n/64 gram eller
  • N2O: 28 gram n/ 16 gram eller
  • N2ANTINGEN3: 28 gram n/ 48 gram eller
  • N2ANTINGEN5: 28 gram n/ 80 gram eller
Det kan tjäna dig: hypofysyra (H3PO2): egenskaper, användningar och reagens

Låt oss glömma kväve och fokusera på syre gram:

  • 2 (nr): 32 gram eller
  • 2 (Nej2): 64 gram eller
  • N2O: 16 gram eller
  • N2ANTINGEN3: 48 gram eller
  • N2ANTINGEN5: 80 gram eller

Att vara förhållandet mellan massorna eller lika med 32: 64: 16: 48: 80. För att förenkla det delar vi alla dess antal bland de minsta, 16, som 2: 4: 1: 3: 5.

Det vill säga det finns: 2 gånger mer syre i nr än i n2Eller 4 gånger mer syre i nr2 det i n2Eller, 3 gånger mer syre i n2ANTINGEN3 det i n2Eller, och 5 gånger mer syre i n2ANTINGEN5 det i n2ANTINGEN. Återigen har vi små hela siffror, allt från 1 till 5.

Begränsningar

Lagen i flera proportioner är inte alltid uppfyllda. Till exempel är de molära massorna eller atomvikterna i elementen inte hela figurer, men har många decimaler. Detta modifierar de beräknade förhållandena helt, som upphör att vara enkla.

På samma sätt uppfylls inte lagen för tunga föreningar, till exempel vissa kolväten. Till exempel undecano, celvaH24, har 1.0083 eller 121/120 gånger mer väte än dekanen, c10H22, vars förhållande består av 121 och 120, som överstiger dussin; De är inte små hela siffror.

Och slutligen misslyckas lagen med icke -stökiometriska föreningar, som med många oxider och sulfider.

Slutsats

De flera proportioner lagen säger att när två element bildar mer än en förening är de olika massorna av ett element som kombineras med samma massa för det andra elementet i en del av ett litet antal.

Referenser

  1. Whitten, Davis, Peck & Stanley. (2008). Kemi. (8: e upplagan.). Cengage Learning.
  2. Wikipedia. (2020). Lag i flera proportioner. Hämtad från: i.Wikipedia.org
  3. Redaktörerna för Enyclopaedia Britannica. (2020). Lag i flera proportioner. Återhämtat sig från: Britannica.com
  4. Kemi. (4 juni 2019). Lag om flera proportioner av Dalton. Återhämtat sig från: ChemistryGod.com
  5. Garcia nissa. (2020). Lag i flera proportioner: Definition & exempel. Studie. Återhämtat sig från: studie.com