Matematik

De Morgan Laws

De Morgan Laws

Vi förklarar vad Morgan's lagar är, vi demonstrerar dem och sätter exempel

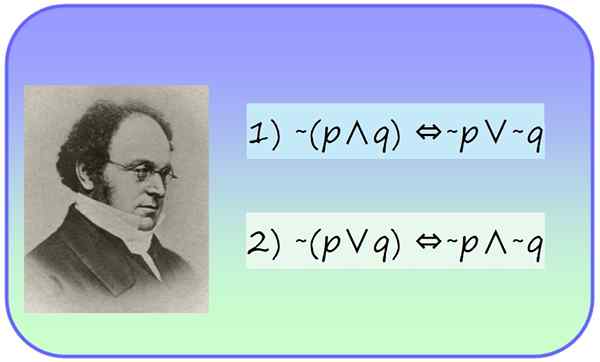Figur 1.- Matematikern Augustus av Morgan (1806-1871) och hans lagar om propositionell logik. Källa: f. Zapata.

Vad är de Morgan's lagar?

De Morgan's lagar är två logiska lagar som tillhör den propositionella logiken som formulerades av den engelska matematikern Augustus i Morgan (1806-1871). De fastställer följande med avseende på ett sammansatt logiskt förslag:

  1. Motsatsen till en konjunktion motsvarar den disjunktion som bildas med motsatserna eller förnekningarna av förslagen som utgör konjunktionen.
  2. Förnekande av disjunktion kan uttryckas som en konjunktion som består av motsatser eller förnekande av förslagen som är involverade i disjunktionen.

I notationen av propositionell logik uttrycks de Morgan's lagar på ett kompakt och mer formellt sätt som detta:

  1. ∼ (p ∧ q) ⇔ ∼P ∨q
  2. ∼ (p ∨ q) ⇔ ∼P ∧q

Vad dessa lagar uttrycker är att antingen i förnekande av konjunktion eller disjunktion motsvarar resultatet att förneka var och en av de deltagande förslagen separat och investera det kontakt som länkar dem.

För en bättre förståelse av De Morgan's lagar är det nödvändigt att granska innebörden av förslagen och symbolerna som används i propositionell logik för att se hur dessa lagar bekvämt gäller.

Logisk notation

Det grundläggande verktyget för propositionell logik är förslagen. Ett logiskt förslag är ett uttalande som medger ett riktigt värde, Oavsett om det är sant eller falskt, men inte båda samtidigt. I detta är ingen tvetydighet tillåten, det vill säga det kan inte vara tveksamt.

Ett förslag betecknas med en gemener, som i följande exempel:

  • F: Mexico City är Mexikos huvudstad (sant).
  • F: Genom att lägga till 2 och 3 erhålls 4 (falska).
  • S: Alla däggdjur är landdjur (falska).
Kan tjäna dig: Hepagon

Det finns också mer komplexa förslag, som är strukturerade genom användning av enkla förslag, till exempel dessa:

  • F: Carlos går på bio om den inte regnar.
  • F: Ana är kemist eller marinbiolog.
  • S: Juan går till middag eller Pedro kommer att se spelet på TV.

Logiska kontakter

Logiska kontakter är symboler som används för att länka enkla förslag och bygger därmed mer komplexa förslag. I propositionell logik har var och en av dem en speciell betydelse.

De mest använda kontakterna är konjunktion, disjunktion, exklusiv disjunktion, förnekelse, villkor och bi-konditionalitet.

Samband

Konjunktionen betecknas med en inverterad "V" -brev. Ett sammansatt förslag genom en konjunktion symboliseras p ∧ q, enligt följande:

  • P ∧ Q: Mexico City är huvudstaden i Mexiko och är i Nordamerika.

Det är lätt att identifiera här att P är "Mexico City är huvudstaden i Mexiko" och Q är "är i Nordamerika".

Åtskiljande

Två typer av disjunktion skiljer sig: de svaga och exklusiva. En svag disjunktion Det symboliseras av ∨ och i logisk notation skulle det vara p ∨ q. Exempel på denna typ av disjunktion är:

  • P ∨ Q: Juan är en fotbollsspelare eller Juan är en tennisspelare.

Istället exklusiv disjunktion Det symboliseras av tecken ⊻ och innebär att ett av förslagen måste uteslutas, till exempel:

P ⊻ Q: Alicia är 20 år eller Alicia är 22 år gammal.

Skillnaden mellan båda typerna är tydlig, i exklusiv disjunktion, ett av förslagen utesluts, eftersom om Alicia är 20 år kan han inte vara 22 och vice versa. Å andra sidan, i den svaga disjunktionen, kan Juan vara fotbollsspelare och tennisspelare samtidigt.

Avslag

Genom att sätta symbolen ∼ ett förslag förnekas detta, som i:

  • F: ∼ (Veracruz är huvudstaden i Mexiko).

Det läses som "Veracruz är inte Mexikos huvudstad". Andra sätt att uttrycka ett förnekande, bortsett från "nej", är genom fraser som "är falskt", "det är en lögn som" och "det är inte sant att".

Kan tjäna dig: linjär interpolation

Villkor

De är sammansatta förslag som vanligtvis använder orden "ja" och "då ..." för att länka två förslag där det finns villkor eller inblandning. Den del av förslaget som skrivs omedelbart efter "ja" är föregående Vinka hypotes av förslaget och vad som är efter termen "då" är slutsats antingen följd.

Symbolen som används för villkor är pilen från vänster till höger "→", därför representeras en villkor mellan två förslag som p → q, som kan läsas som "om p, då q". Till exempel:

P → Q: Om det regnar under eftermiddagen kommer jag inte att spela tennis.

Tvåkonditionalitet

I denna typ av förslag används frasen "ja, och endast om" för att ansluta två förslag, kallas första och andra biconditionalmedlem. Den symbol som används är den dubbelriktade pilen "↔".

De två förslagen som är kopplade till "ja, och endast om" kallas respektive först och andra medlem och bi-konditionaliteten för två förslag p och q förblir som p ↔ q. Till exempel:

P ↔ Q: Maria gillar att cykla om och bara om dagen är solig.

Demonstration av de Morgan's lagar

De Morgan's lagar är en del av logiska ekvivalenser och kan demonstreras genom sanningsborden, som används för att veta sanningen (sant eller falskt) värde på ett förslag.

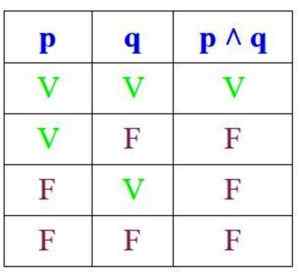
Eftersom konjunktionen endast är sant när P och Q är sanna är dess sanningsstabell:

Å andra sidan, i disjunktion, är förslaget sant om P och Q är sant eller om åtminstone en av dem är, men det är falskt om båda är:

Kan tjäna dig: permutationer utan upprepning: formler, demonstration, övningar, exempel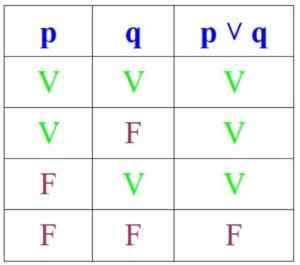

Nu förvandlar förnekande sanningen till falska och vice versa. I detta fall är sanningsvärdena för ∼ (p ∧ q) och ∼ (p ∨ q) motsatsen till sanningsvärdena (p ∧ q) och (p ∨ q):

Och det måste verifieras att dessa resultat erhålls vid utförande av respektive sanningstabeller för (∼ p ˅ ∼ q) och (∼ p ˄ ∼ q):

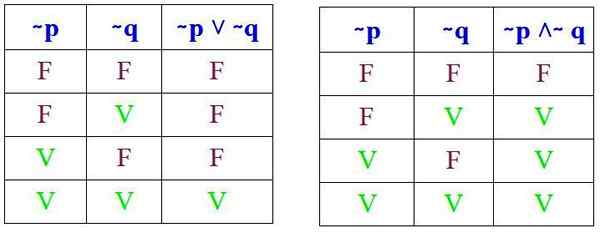
Och faktiskt, när man jämför respektive sanningstabeller, observeras att De Morgan's lagar är uppfyllda. Nu kommer två exempel på dess tillämpning att ses.

Löst exempel 1

Tillämpa de Morgan's lagar för att hitta motsvarande uttryck för: ∼ (∼P ˅ ∼Q)

  • Lösning

Det givna uttrycket jämförs ∼ (∼P ˅ ∼Q) med Morgan's Law:

∼ (p ∨ q) ⇔ ∼P ∧q

Och det observeras att förnekandet redan ligger utanför parentesen i båda fallen, därför följs instruktionerna i lagen: den vägrar ∼P, förnekar ∼Q och kontakten ändras:

∼ (∼P ˅ ∼Q) ⇔ ∼ (∼P) ∧ ∼ (∼q) ⇔ p ∧ q

Löst exempel 2

Bestäm motsvarande uttryck av ∼ [∼P ˄ ∼ (∼q)] ≡

  • Lösning

Först förenklas ∼q -förnekandet:

∼ [∼P ˄ ∼ (∼q)] ⇔ ∼ [∼P ˄ q]

Eftersom det redan finns ett förnekande utanför konsolen jämförs det resulterande uttrycket med Morgan's Law: ∼ (p ∧ q) ⇔ ∼P ∨q

För att lösa ∼ [∼P ˄ q] måste du förneka ∼P, förneka Q och ändra kontakten:

∼ [∼P ˄ q] ⇔∼ (∼P) ∨ ∼Q ⇔ p ˅ ∼q

Referenser

  1. Becerra, j.M.  UNAM LOGIC NOTER.
  2. Lysande. Från Morgan's Laws. Återhämtat sig från: lysande.org.
  3. Elektronikhandledning. Av Morgan's Theorem. Återhämtat sig från: elektronik-mormaler.Ws.
  4. López, f. Introduktion till matematisk logik. Återhämtat sig från: YouTube.com
  5. Muñoz, c. Introduktion till logik. Hämtad från: webbplatser.Ucm.är.