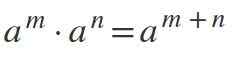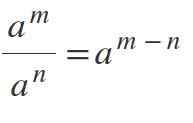Exponenternas lagar

Vilka är exponenternas lagar?

De Exponenternas lagar Det är de som gäller för det numret som indikerar hur många gånger ett basnummer måste multipliceras av sig själv. Exponenter är också kända som krafter. Förstärkningen är en matematisk operation som bildas av en bas (a), exponenten (m) och kraften (b), vilket är resultatet av operationen.

Exponenter används vanligtvis när mycket stora mängder används, eftersom det inte är något annat än förkortningar som representerar multiplikationen av samma antal en viss mängd gånger. Exponenter kan vara både positiva och negativa.

Vad är exponenter i matematiska operationer?

Som nämnts ovan är exponenter en förkortad form som representerar multiplikation av siffror för sig själva, där exponenten endast hänför sig till vänsternumret. Till exempel:

2³ = 2*2*2 = 8

I så fall är nummer 2 basen för kraften, som kommer att multipliceras 3 gånger såsom indikeras av exponenten, belägen i det övre högra hörnet av basen. Det finns olika sätt att läsa uttrycket: 2 upphöjda till 3 eller 2 höjda till kuben.

Exponenterna indikerar också antalet gånger som kan delas upp och för att skilja denna operation från multiplikationen som exponenten bär minus (-) -tecknet framför sig själv (det är negativt), vilket innebär att exponenten är i nämnaren för en bråkdel. Till exempel:

2^{- 4} = 1/2*2*2*2 = 1/16

Detta bör inte förväxlas med fallet där basen är negativ, eftersom det kommer att bero på om exponenten är jämnt eller udda för att avgöra om kraften kommer att vara positiv eller negativ. Således måste du:

- Om exponenten är jämn kommer kraften att vara positiv. Till exempel:

(-7)² = -7 _* -7 = 49.

- Om exponenten är udda kommer kraften att vara negativ. Till exempel:

(-2)⁵ = (-2)*(-2)*(-2)*(-2)*(-2) = -32.

Det finns ett speciellt fall där om exponenten är lika med 0 är kraften lika med 1. Det finns också möjligheten att basen är 0; I så fall, beroende på exponenten, kommer kraften att inte bestämmas eller inte.

För att utföra matematiska operationer med exponenter är det nödvändigt.

Vilka är exponenternas lagar?

Första lagen: Exponent Power lika med 1

När exponenten är 1 kommer resultatet att vara samma värde som basen: a¹ = a.

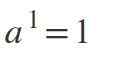
Exempel

9¹ = 9.

22¹ = 22.

895¹ = 895.

Andra lagen: Exponent Power lika med 0

När exponenten är 0, om basen skiljer sig från noll, kommer resultatet att vara: a⁰ = 1.

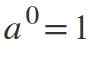
Exempel

1⁰ = 1.

323⁰= 1.

1095⁰ = 1.

Tredje lag: Negativ exponent

Eftersom exponenten är negativ kommer resultatet att vara en bråkdel, där kraften kommer att vara nämnaren. Till exempel om M är positiv, då^-m = 1/a^m.

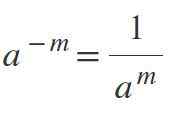
Exempel

- 3^-1 = 1/3.

- 6^-2 = 1/6² = 1/36.

- 8^-3 = 1/8³ = 1/512.

Fjärde lagen: Multiplikation av lika krafter med samma

För att multiplicera krafter där baserna är desamma och skiljer sig från 0, upprätthålls basen och exponenterna läggs till: a^m _* tillⁿ = a^m+n.    

Exempel

- 4⁴ _* 4³ = 4⁴⁺³ = 4⁷

- 8¹ _* 8⁴ = 8¹⁺⁴ = 8⁵

- 2² _* 2⁹ = 2²⁺⁹ = 2^elva

Femte lagen: Power Division med samma bas

För att dela krafter där baserna är desamma och skiljer sig från 0, baseras basen och exponenterna subtraheras enligt följande: a^m tillⁿ = a^M-n.    

Exempel

- 9² / 9¹ = 9 ^(tjugoett) = 9¹.

- 6^femton / 6¹⁰ = 6 ^{(15 - 10)} = 6⁵.

- 49¹² / 49⁶ = 49 ^{(12 - 6)} = 49⁶.

Sjätte lag: Multiplikation av olika krafter med en annan bas

I denna lag finns det motsatsen till vad som uttrycks i det fjärde; Det vill säga om du har olika baser men med samma exponenter multipliceras baserna och exponenten upprätthålls: a^m _* b^m = (a_*b) ^m.

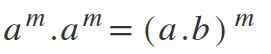
Exempel

- 10² _* tjugo² = (10 _* tjugo)² = 200².

- Fyra fem^elva _* 9^elva = (45*9)^{11 =} 405^elva.

Ett annat sätt att representera denna lag är när en multiplikation är hög till en makt. Således kommer exponenten att tillhöra var och en av villkoren: (a_*b)^m= a^m_* b^m.

Exempel

- (5_*8)⁴ = 5⁴ _* 8⁴ = 40⁴.

- (23 * 7)⁶ = 23⁶ _* 7⁶ = 161⁶.

Sjunde lagen: Olika maktavdelningar

Om du har olika baser men med samma exponenter är baserna uppdelade och exponenten upprätthålls:^m / b^m = (a / b)^m.

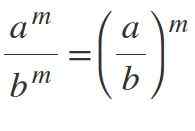
Exempel

- 30³ / 2³ = (30/2)³ = 15³.

- 440⁴ / 80⁴ = (440/80)⁴ = 5.5⁴.

På samma sätt, när en division är hög för en makt, kommer exponenten att tillhöra i var och en av villkoren: (a / b) ^m = a^m /b^m.

Exempel

- (8/4)⁸ = 8⁸ / 4⁸ = 2⁸.

- (25/5)² = 25² / 5² = 5².

Det finns fallet där exponenten är negativ. Så för att vara positiv investeras värdet på telleren med nämnaren, enligt följande:

- (A / B)^-n = (b / a)ⁿ = Bⁿ tillⁿ.

- (4/5) ^-9 = (5/4) ⁹ = 5⁹ / 4⁴.

Åttonde lagen: maktens makt

När du har en kraft som höjs till en annan kraft -är det, två exponenter samtidigt -basen upprätthålls och exponenterna multipliceras: (a^m)ⁿ= a^m*n.

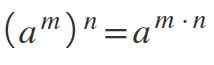
Exempel

- (8³)² = 8 ^(3*2) = 8⁶.

- (13⁹)³ = 13 ^(9*3) = 13²⁷.

- (238¹⁰)¹² = 238^{(10 * 12)} = 238¹²⁰.

Nionde lag: fraktionerad exponent

Om kraften har en exponent en bråkdel, löses detta genom att förvandla den till en N-Esima-rot, där telleren förblir som exponent och nämnaren representerar rotindexet:

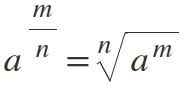
Exempel

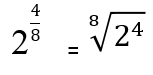
Löst övningar

Övning 1

Beräkna operationerna mellan de krafter som har olika baser:

2⁴ _* 4⁴ / 8².

Lösning

Tillämpning av reglerna för exponenterna multipliceras baserna i telleren och exponenten upprätthålls, så här:

2⁴ _* 4⁴ / 8²= (2_*4)⁴ / 8²  = 8⁴ / 8²

Nu, eftersom det finns lika baser, men med olika exponenter upprätthålls basen och exponenterna subtraheras:

 8⁴ / 8² = 8^{(4 - 2)} = 8²

Övning 2

Beräkna driften mellan höga krafter till en annan kraft:

(3²)³ _* (2 _* 6⁵)^-2 _* (2²)³

Lösning

Tillämpa lagarna måste du:

(3²)³ _* (2 _* 6⁵)^-2 _* (2²)³

= 3⁶ _* 2^-2 _* 2^-10 _* 2⁶

= 3⁶ _* 2^{(-2) + (- 10)} _* 2⁶

= 3⁶ _*  2^-12 _* 2⁶

= 3⁶ _* 2^{(-12) + (6)}

= 3⁶ _* 2⁶

= (3_*2)⁶

= 6⁶

= 46.656

Referenser

1. Aponte, g. (1998). Grundläggande matematikfundament. Pearson Education.
2. Corbalán, f. (1997). Matematik tillämpad på vardagen.
3. Jiménez, J. R. (2009). Matematik 1 september.
4. Max Peters, W. L. (1972). Algebra och trigonometri.
5. Rees, s. K. (1986). Reverte.