Blockalgebra -element, exempel, övningar löst

han Blockalgebra Det hänvisar till uppsättningen operationer som utförs genom block. Dessa och några fler element tjänar till att schematiskt representera ett system och enkelt visualisera ditt svar på en specifik post.

I allmänhet innehåller ett system olika elektriska, elektroniska och elektromekaniska element, och var och en av dem, med deras respektive funktion och position i systemet, liksom hur de är relaterade, schematiseras genom funktionella block.

Figur 1.

I figuren ovan finns ett mycket enkelt system, som består av en insignal x (er), som kommer in i blocket med överföringsfunktionen g (er) som modifierar det och producerar utgången y (er).

Det är bekvämt att representera signalerna och deras resa genom systemet genom pilar som kommer in och lämnar varje block. Vanligtvis är signalflödet riktat från vänster till höger.

Fördelen med denna typ av schema är den visuella hjälp som det ger för att förstå systemet, även om det inte utgör en fysisk representation av samma. Faktum är att blockdiagrammet inte är unikt, eftersom enligt synvinkel kan till och med flera diagram av samma system dras.

Det kan också hända att samma diagram används för flera system som inte nödvändigtvis är relaterade till varandra, förutsatt att dess beteende korrekt beskriver. Det finns olika system vars svar är liknande i många aspekter, till exempel en LC-krets (induktor-kanal) och ett mass-resortsystem.

[TOC]

Vad är ett blockdiagram?

Systemen är vanligtvis mer komplicerade än i figur 1, men blockalgebra ger en serie enkla regler för att manipulera systemschemat och minska det till dess enklaste version.

Som förklarats i början använder diagrammet block, pilar och cirklar för att upprätta förhållandet mellan varje systemkomponent och flödet av signalerna som går igenom det.

Block Algebra gör det möjligt att jämföra två eller flera signaler genom summa, subtraktion och multiplikation av dem, samt analysera det bidrag som varje komponent gör till systemet.

Tack vare detta är det möjligt att reducera hela systemet till en enda insignal, en unik överföringsfunktion som helt beskriver systemåtgärden och motsvarande utgång.

Det kan tjäna dig: astroclymics: historia, vilka studier, grenar

Blockdiagramelement

Elementen i blockdiagrammet är följande:

Signalen

Signalerna är mycket varierande, till exempel är det vanligt att det är en elektrisk ström eller en spänning, men det kan vara ljust, sund och mer. Det viktiga är att det innehåller information om ett visst system.

Signalen betecknas med en stor bokstav om det är en funktion av variabeln s av Laplace Transform: X (S) (se figur 1) eller med små bokstäver om den är baserad på tid t, Som x (t).

I blockschemat representeras ingångssignalen av en pil riktad mot blocket, medan utgångssignalen, betecknad som y (er) eller (t), indikeras med en utgående pil.

Både ingångs- och utsignalen är unik och adressen i vilken informationsflödena bestäms av pilens riktning. Och algebra är densamma för någon av de två variablerna.

Kvarteret

Blocket representeras av en fyrkant eller en rektangel (se figur 1) och kan användas för att utföra operationer eller implementera överföringsfunktionen, som vanligtvis betecknas med kapitalbokstaven G. Denna funktion är en matematisk modell som svaret som erbjuds av systemet beskrivs före en inträdesignal.

Överföringsfunktionen kan uttryckas i termer t såsom g (t) eller variabeln s som G (s).

När ingångssignalen x (er) anländer till blocket multipliceras den med överföringsfunktionen och förvandlas till utgångssignalen y (er). Matematiskt uttrycks det enligt följande:

Och (s) = x (s).G (s)

På samma sätt är överföringsfunktionen förhållandet mellan Laplace -transformationen av utsignalen och Laplace -transformen av insignalen, förutsatt att systemets initiala förhållanden är noll:

G (s) = y (s) / x (s)

Summan

Summan eller sommaren symboliseras av en cirkel med ett kors inuti. Det används för att kombinera, av summor och subtraktion, två eller flera signaler. I slutet av pilen som symboliserar signalen placeras ett tecken + direkt om den signalen läggs till eller ett tecken - om det subtraheras.

I följande figur finns det ett exempel på hur sommaren fungerar: du har insignalen X, till vilken signaler A och B läggs till, vilket får ett resultat avfarten och, som algebraiskt är lika med:

Kan tjäna dig: vertikalt skott: formler, ekvationer, exempel

Y = x+a+b

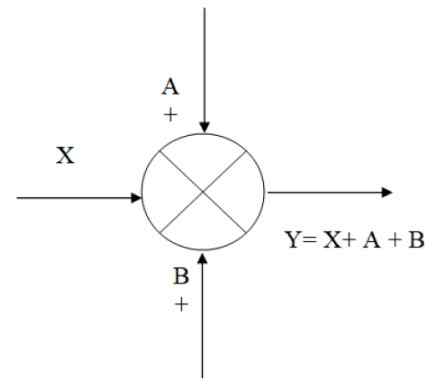figur 2. Exempel på en verkställighet. Källa: f. Zapata.

Grenpunkt

Det kallas också Bifurkationspunkt. I den distribueras signalen som kommer ut ur ett block till andra block eller till en plommon. Det representeras av en punkt som placeras på signalens pil och en annan pil kommer från den som omdirigerar signalen mot en annan del.

Figur 3. Grenpunkt. Källa: f. Zapata.

Exempel på block i blockalgebra

Som förklarats tidigare är tanken att uttrycka systemet genom blockdiagrammet och minska det för att hitta överföringsfunktionen som beskriver den. Följande är reglerna för blockalgebra för att förenkla diagrammen:

Kaskadblock

När du har en signal som passerar successivt genom G -blocken₁, G₂, G₃..., det reduceras till ett unikt block vars överföringsfunktion är produkten från G₁, G₂, G₃..

I följande exempel kommer Signal X (S) in i det första blocket och dess utgång är:

OCH₁(s) = x (s).G₁(S)

Figur 4. Två kvarter i vattenfallet. Källa: f. Zapata.

I sin tur och₁(s) Ange G -blocket₂(S), vars avgång är:

OCH₂(s) = x (s).G₁(S). G₂(S)

Proceduren är giltig för n kaskadblock:

OCH_n (s) = x (s). G₁(S).G₂(S) ... G_n(S)

Parallellt med block

I det vänstra diagrammet signalerar x (s) bifurca för att komma in i G -blocken₁(S) och g₂(S):

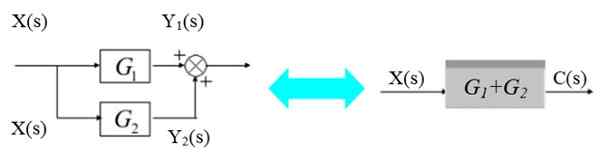Figur 5. Två block parallellt. Källa: f. Zapata.

De respektive utgångssignalerna är:

OCH₁(s) = x (s).G₁(S)

OCH₂(s) = x (s).G₂(S)

Dessa signaler läggs till för att få:

C (s) = y₁(S) +₂(s) = x (s).[G₁(s) + g₂(S)]

Som visas i höger -rätt diagram.

Flytta en friare till vänster

En sommar kan flytta till vänster om blocket enligt följande:

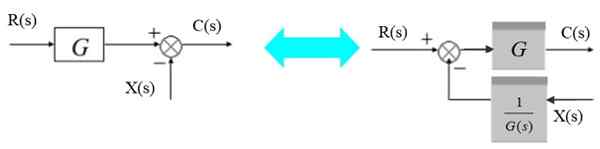Figur 6. Flytta tillägget till vänster om blocket. Källa: f. Zapata.

Till vänster är utsignalen:

C (s) = r (s). G (s) - x (s)

Motsvarande till höger:

C (s) = [r (s) - x (s)/g (s)]].G (s)

Flytta höger till höger

Sommaren kan flytta till höger om blocket så här:

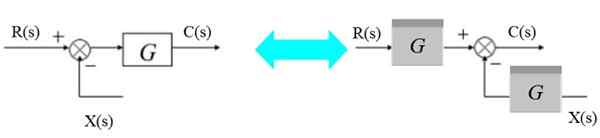Figur 7. Flytta en tomt till höger om blocket. Källa: f. Zapata.

Till vänster har du: [r (s) - x (s)].G (s) = c (s)

Kan tjäna dig: Archimedes Princip: Formel, Demonstration, Applications

Och till höger:

R (s). G (s) - x (s).G (s) = c (s)

Flytta en förgrenande punkt från vänster till höger

För att förskjuta bifurcationspunkten från vänster till höger om blocket räcker det att observera att utgången c (er) till höger är produkt x (er).G (s). När du vill bli x (s) igen multipliceras det med det omvända av g (s).

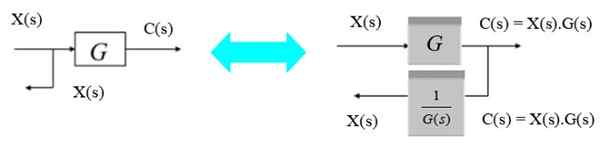Figur 8. Flytta en grenpunkt från vänster till höger. Källa: f. Zapata.

Flytta en förgrenande punkt från höger till vänster

Alternativt kan bifurcationspunkten röra sig från höger till vänster enligt följande:

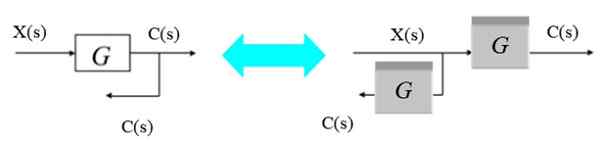Figur 9. Flytta en grenpunkt från höger till vänster. Källa: f. Zapata.

Eftersom utgången från bifurcationen vill erhålla C (er), är ett nytt block G (er) helt enkelt isär vid en bifurcationspunkt till vänster om det ursprungliga blocket.

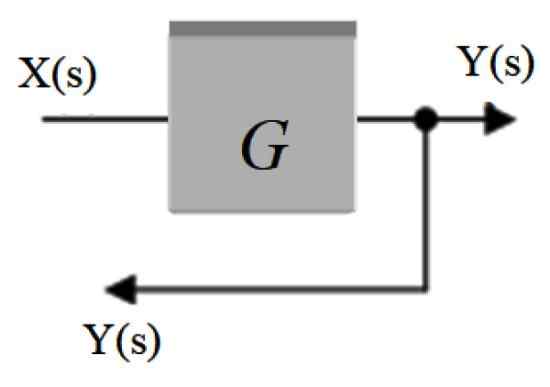
System med feedback

I följande system matas utgångssignalen C (er) genom undergiven till vänster:

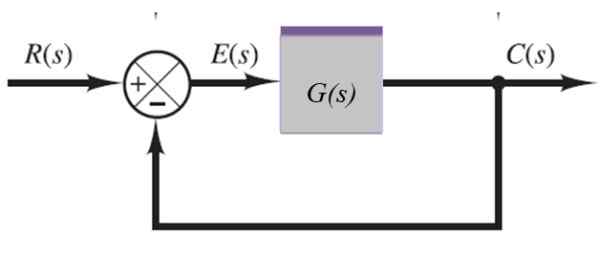Figur 10. System med feedback. Källa: f. Zapata.

C (s) = e (s).G (s)

Men:

E (s) = r (s) -c (s)

Att ersätta detta uttryck i föregående ekvation är: c (s) = [r (s) -c (s)]].G (s), från vilken c (s) kan rensas:

C (s) + c (s).G (s) = r (s).G (s) → c (s). [1 + g (s)] = r (s).G (s)

C (s) = r (s).G (s) / [1 + g (s)]

Eller växelvis:

C (s) / r (s) = g (s) / [1 + g (s)]]]

Grafiskt, efter att ha förenklat det är:

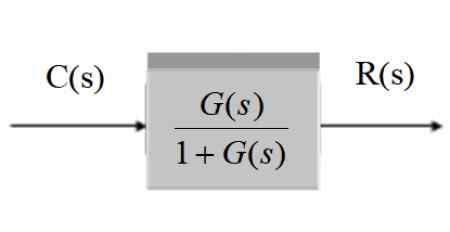Figur 11. Förenkling av ett system med feedback. Källa: f. Zapata.

System med feedback och givare

Givaren består av överföringsfunktionen H (er):

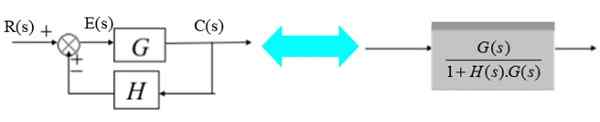Figur 12. System med feedback och givare. Källa: f. Zapata.

I det högra diagrammet är utgångssignalen C (er):

C (s) = e (s). G (s) med e (s) = r (s) - c (s).H (s)

Så:

C (s) = [r (s) - c (s). H (s)]. G (s)

C (s) [1+ h (s).G (s)] = r (s).G (s)

Därför kan c (er) rensas av:

C (s) = g (s).R (s) / [1+ h (s).G (s)]

Och överföringsfunktionen kommer att vara:

G (s) / [1+ h (s).G (s)]

Som visas i det förenklade högerdiagrammet.

Löst övningar

Övning 1

Hitta överföringsfunktionen för följande system:

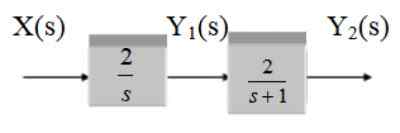Figur 13. Två blocksystem i vattenfall. Källa: f. Zapata.

Lösning

Det är två kaskadblock, därför är överföringsfunktionen produkten från funktionerna g₁ och g₂.

Du måste:

G₁ = 2/s

G₂ = 2 /(S+1)

Därför är den sökande överföringsfunktionen:

G (s) = 4 / [s (s+1)]

Övning 2

Minska följande system:

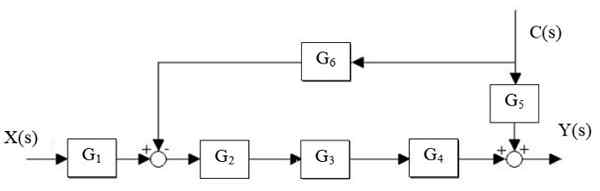Figur 14. Förenkling av ett system. Källa: f. Zapata.

Lösning

Först reduceras G -kaskaden₂, G₃ och g_4, Och den parallella g är separerad₅ och g₆:

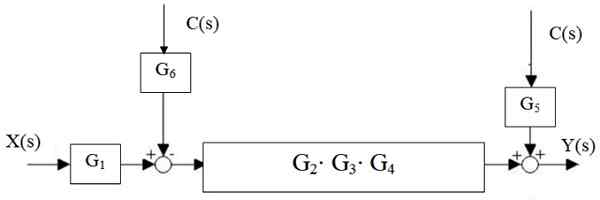Figur 15. Central Waterfall Reduction. Källa: f. Zapata.

Sedan, friaren till vänster om G -blocket₂ ⋅g₃ ⋅ g₄ Han rör sig till höger:

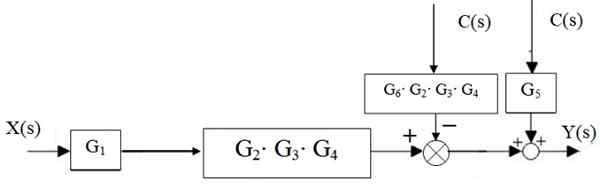Figur 16. Överföring av administrationen. Källa: f. Zapata.

Somrarna till höger reduceras till en, liksom kaskadblocken:

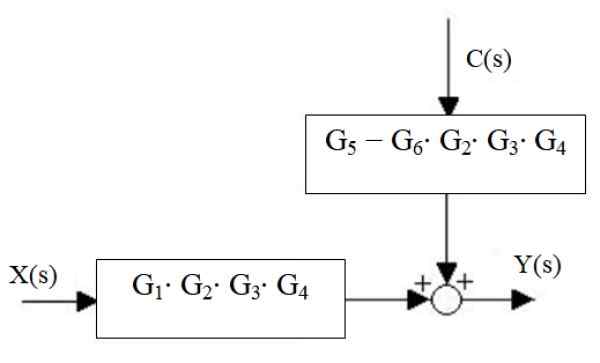Figur 17. Minskning av det nya vattenfallet och somrarna på höger. Källa: f. Zapata.

Slutligen är systemutgången:

Och (s) = x (s) ⋅g₁⋅ g₂ ⋅g₃ ⋅ g₄ + C (s) ⋅ [g₅ - G₆ ⋅ g₂ ⋅g₃ ⋅ g₄]

Referenser

1. Alaydi, j. Systemblockdiagramkontroll. Återhämtad från: webbplats.iugaza.Edu.$.
2. Bolton, W. 2006. Kontrollteknik. 2: a. Utgåva. Alfa -omega.
3. Cwalinsky, J. Introduktion till systemblockalgebra. Återhämtat sig från: cedengineering.com.
4. Pappa. Blockerar diagram. Återhämtat sig från: Dademuch.com.
5. Ogata, k. 2010. Modern kontrollteknik. Femte. Utgåva. Pearson.