Vridmoment

Vi förklarar vad som är tiden för torsion, dess egenskaper, formler, enheter, applikationer och sätter övningar för att lösa

Vad är tiden för vridning?

han Vridmoment, Vridmoment eller kraft av kraft är förmågan hos en kraft att orsaka en sväng. Etymologiskt kallas det vridmoment som en härledning av det engelska ordet Vridmoment, från latin Vridmoment (vrida).

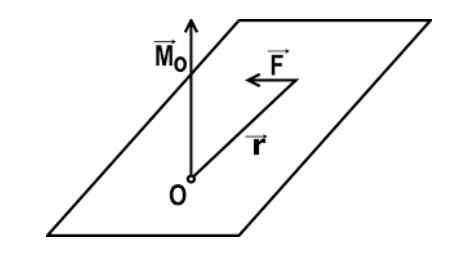
Tiden för torsion (med avseende på en viss punkt) är den fysiska storleken som är resultatet av att utföra vektorprodukten mellan positionsvektorerna i den punkt där kraften appliceras och den för kraften som utövas (i den angivna ordningen). Detta ögonblick beror på tre huvudelement.

Det första av dessa element är storleken på den applicerade kraften, den andra är avståndet mellan den punkt där den gäller och punkten med avseende på kroppen roterar (även kallad spakarmen), och det tredje elementet är vinkelapplikationen av nämnda kraft.

Större kraft, större sväng orsakas. Detsamma gäller för spakarmen: ju större avståndet mellan den punkt där kraften och punkten appliceras med avseende på den som produceras av svängen, desto större kommer detta.

Logiskt sett är tid för torsion av särskilt intresse för konstruktion och industri, liksom är närvarande i otaliga hemmapplikationer, till exempel när en mutter pressas med en engelsk nyckel.

Formler

Det matematiska uttrycket av momentet av vridning av en kraft med avseende på en punkt eller ges av: m = r x f

I detta uttryck är R den vektor som förenar punkten med O med punkten P för tillämpningen av kraften, och F är vektorn för den applicerade kraften.

Kan tjäna dig: elektrodynamik

Måtenhetsenheterna är n ∙ m, som även om det är dimensionellt motsvarande juli (j), har en annan betydelse och inte bör förvirras.

Därför tar momentmomentmodulen värdet som ges av följande uttryck:

M = R ∙ F ∙ SEN α

I detta uttryck är a vinkeln mellan styrkavektorn och vektorn R eller spakarm. Tiden för torsion anses vara positiv om kroppen kretsar i motsatt riktning till klockålarna; Tvärtom, det är negativt när det vänder sig till ett schema.

Enheter

Måttenheten på vridningen är produkten från en kraftenhet med en avståndsenhet. Specifikt används i det internationella enhetssystemet Newton Metro vars symbol är n • m.

På dimensionell nivå kan Newton -tunnelbanan tyckas motsvara juli; Men i något fall bör juli användas för att uttrycka stunder. Juli är en enhet för att mäta verk eller energier som från en konceptuell synvinkel skiljer sig mycket från torsionsstunder.

På liknande sätt presenterar torsionsmomentet en vektorkaraktär, som är både arbete och skala energi.

Vridmomentegenskaper

Från det sett följer det att momentet av vridning av en styrka med avseende på en punkt representerar kapaciteten hos en kraft eller uppsättning krafter att modifiera rotationen av nämnda kropp runt en axel som passerar genom punkten.

Därför genererar torsionsmomentet en vinkelacceleration på kroppen och är en storlek av en vektorkaraktär (så det definieras från en modul, en riktning och en känsla) som finns i mekanismerna som har utsatts för torsion eller flexion.

Det kan tjäna dig: Vy Canis Majoris: Discovery, Egenskaper, struktur, träning och utveckling

Tiden för torsion kommer att ogiltigförklaras om styrkavektorn och vektorn har samma riktning, eftersom värdet på SEN α ​​i så fall kommer att bli ogiltigt.

Resulterande vridmoment

Med tanke på en viss kropp som en serie krafter agerar, om de tillämpade styrkorna agerar i samma plan, är momentet av vridning som är resultatet av tillämpningen av alla dessa krafter; Det är summan av vridmomenten som en följd av varje kraft. Därför är det uppfyllt att:

M_T = ∑ m = m₁ + M_{2 +} M₃ +..

Naturligtvis är det nödvändigt att ta hänsyn till kriteriet för tecken för torsionsstunder, som förklarats ovan.

Ansökningar

Vridmomentet finns i applikationer så varje dag som pressar en mutter med en engelsk nyckel, eller öppnar eller stänger en kran eller en dörr.

Men dina applikationer går mycket längre; Tiden för torsion finns också i maskinens axlar eller i resultatet av de ansträngningar som balkarna utsätts för. Därför är dess tillämpningar inom bransch och mekanik många och varierande.

Löst övningar

Nedan följer ett par övningar för att underlätta förståelsen av ovanstående förklarade.

Övning 1

Med tanke på följande figur där avståndet mellan punkt O och punkterna A och B är respektive 10 cm och 20 cm:

a) Beräkna värdet på vridmomentmodulen med avseende på punkten eller om en kraft på 20 n tillämpas vid punkt a.

b) Beräkna vad som ska vara värdet på den kraft som appliceras i B för att uppnå samma tid av torsion som erhölls i föregående avsnitt.

Kan tjäna dig: kontinuitetsekvation

Lösning

Först bör data till internationella systemenheter passera.

r_TILL = 0,1 m

r_B = 0,2 m

a) För att beräkna vridmomentet använder vi följande formel:

M = R ∙ F ∙ SEN α ​​= 0,1 ∙ 20 ∙ 1 = 2 N ∙ M

b) För att bestämma den begärda kraften, fortsätt på liknande sätt:

M = R ∙ F ∙ SEN α ​​= 0,2 ∙ F ∙ 1 = 2 N ∙ M

Rensa f det erhålls att:

F = 10 n

Övning 2

En kvinna utför en kraft på 20 N i slutet av en engelsk nyckel 30 cm i längd. Om kraften på kraften med nyckeln till nyckeln är 30 °, vad är tiden för vridning i muttern?

Lösning

Följande formel tillämpas och fungerar:

M = R ∙ F ∙ SEN α ​​= 0,3 ∙ 20 ∙ 0,5 = 3 N ∙ M