Euler -metoden för vad som används av proceduren och övningar

han Euler -metod Det är den mest grundläggande och enkla för de procedurer som används för att hitta ungefärliga numeriska lösningar, till en vanlig differentiell ekvation av den första ordningen, förutsatt att dess initiala tillstånd är känt.

En vanlig differentiell ekvation (EDO) är ekvationen som relaterar en okänd funktion av en enda oberoende variabel med dess derivat.

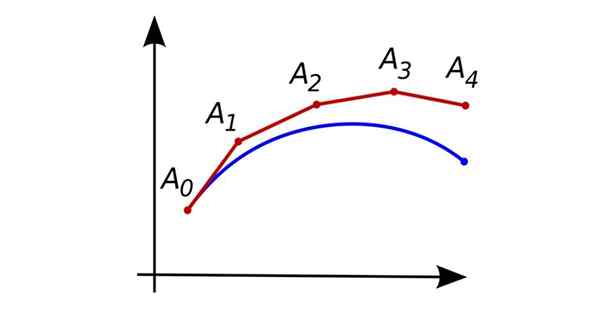
På varandra följande tillvägagångssätt med Eulers metod. Källa: Oleg Alexandrov [Public Domain]

Om det största derivatet som visas i ekvationen är av grad en, är det en vanlig differentiell ekvation av första graden.

Det mest allmänna sättet att skriva en första gradsekvation är:

med det ursprungliga tillståndet:

x = x₀

y = y₀

[TOC]

Vad är Eulers metod?

Idén med Euler -metoden är att hitta en numerisk lösning på differentiell ekvation i intervallet mellan x₀ och x_F .

För det första är intervallet i N+1 -punkter oeniga:

x₀, x₁, x₂, x₃..., x_n

Som erhålls så här:
x_Yo= x₀+Ih

Där h är bredden eller steget för underintervalen:

Ju större antalet n resultatet blir mer exakt, men ett större antal punkter kommer att behövas för att täcka intervallet där vi letar efter lösningen och datortiden växer.

Med det initiala tillståndet är det också möjligt att känna till derivatet i början:

och '(x_antingen) = f (x_antingen, och_antingen)

Detta derivat representerar lutningen för linjen tangent till funktionskurvan y (x) exakt vid punkten:

Ao = (x_antingen, och_antingen)

Sedan görs en ungefärlig förutsägelse av värdet på funktionen y (x) på följande punkt:

och (x₁) ≈ och₁

och_1 = och_antingen +(x₁- x_antingen) f (x_antingen, och_antingen) = y_{antingen +} H f (x_antingen, och_antingen)

Nästa ungefärliga punkt i lösningen som skulle motsvara:

TILL₁ = (x₁, och₁)

Förfarandet upprepas för att få de på varandra följande punkterna

Kan tjäna dig: logaritmisk funktion: egenskaper, exempel, övningar

TILL₂, TILL₃..., x_n

I figuren som visas i början representerar den blå kurvan den exakta lösningen för differentiell ekvation, och den röda representerar de på varandra följande ungefärliga punkterna som erhålls av Euler -proceduren.

Löst övningar

Övning 1

Yo) Vara den differentiella ekvationen:

Med det initiala tillståndet x = a = 0; och_till= 1

Genom att använda Euler -metoden får du en ungefärlig lösning av och I koordinat x = b = 0.5, underdivering av intervallet [a, b] vid n = 5 delar.

Lösning

Numeriska resultat sammanfattas enligt följande:

Där det dras slutsatsen att lösningen och för värde 0.5 är 1.4851.

Obs: För att realisera beräkningarna har den använts SMATH -studio, Gratis gratis användningsprogram.

Övning 2

Ii) Fortsätter med differentiell ekvation i träning i), hitta den exakta lösningen och jämföra den med resultatet som erhålls med Euler -metoden. Hitta felet eller skillnaden mellan det exakta resultatet och det ungefärliga.

Lösning

Med det initiala tillståndet x = a = 0; och_till= 1
Den exakta lösningen är inte särskilt svår att hitta. Det är känt att derivatet av SEN (x) -funktionen är cos (x) -funktionen. Därför kommer lösningen y (x) att vara:

och (x) = sin x + c

För att uppfylla det initiala tillståndet och (0) = 1 måste konstanten vara värd 1. Därefter jämförs det exakta resultatet med det ungefärliga:

Det dras slutsatsen att tillvägagångssättet i det beräknade intervallet har tre betydande noggrannhetssiffror.

Övning 3

Iii) Tänk på differentiell ekvation och dess initiala förhållanden nedan:

och '(x) =- y²

Med det initiala villkoret x₀ = 0; och₀ = 1

Använd Euler -metoden för att hitta ungefärliga värden på lösningen och (x) I intervallet x = [0, 1.5]. Använda steg H = 0.1.

Lösning

Eulers metod är mycket indicerad att användas med ett kalkylblad. I det här fallet kommer vi att använda kalkylbladet för Geogebra, Ett gratis och gratis användningsprogram.

Det kan tjäna dig: sammansatt proportionalitet: Förklaring, tre sammansatta regel, övningar

Tre kolumner (A, B, C) visas i figurens kalkylblad x , Den andra kolumnen representerar variabeln och, och den tredje kolumnen derivatet och'.

Rad 2 innehåller de initiala värdena för X, OCH, OCH' .

Värdet på värde 0.1 Det har placerats i den absoluta positionen cell ($ 4).

Det initiala Y0 -värdet är i cell B2 och Y1 i cell B3. För att beräkna och₁ Formeln används:

och_1 = och_antingen +(x₁- x_antingen) f (x_antingen, och_antingen) = y_{antingen +} H f (x_antingen, och_antingen)

Denna kalkylarkformel skulle vara nummer B3: = B2 + $ D $ 4 * C3.

På liknande sätt skulle Y2 vara i cell B4 och dess formel visas i följande figur:

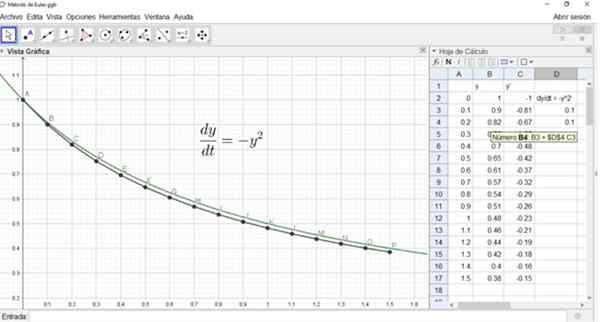
Figuren visar också grafen för den exakta lösningen, och punkter a, b, ..., p för den ungefärliga lösningen med hjälp av Euler -metoden.

Newton Dynamics och Eulers metod

Den klassiska dynamiken utvecklades av Isaac Newton (1643 - 1727). Den ursprungliga motivationen för Leonard Euler (1707 - 1783) att utveckla sin metod var just för att lösa ekvationen i Newtons andra lag i olika fysiska situationer.

Newtons andra lag uttrycks ofta som en sekundär differentiell ekvation:

Var x representerar ett objekts position just nu t. Detta objekt har en massa m och utsätts för en styrka F. Funktionen F Det är relaterat till styrka och massa på följande sätt:

 Även om Euler -metoden i princip var utformad för att lösa först -graders differentiella ekvationer, är det lätt utdragbart till det andra fallet, eftersom det motsvarar ett system med två första gradsekvationer.

Det kan tjäna dig: analytisk geometri

För att tillämpa Euler -metoden krävs initiala tidsvärden t, fart v och position x.

Följande tabell förklarar hur man börjar från initiala värden T1, V1, X1 en tillnärmning av V2 -hastigheten och x2 -positionen kan erhållas, för tillfället T2 = T1+ΔT, där ΔT representerar en liten ökning och motsvarar steget i metoden för Euler.

Övning 4

Iv) Ett av de grundläggande problemen i mekanik är det för ett block av massor som är bundna till en fjäder (eller fjäder) av elastisk konstant K.

Newtons andra lag för detta problem skulle vara så här:

I detta exempel kommer det att tas m = 1 och k = 1 för att förenkla det. Hitta ungefärliga lösningar på positionen x Och hastigheten v Med Eulers metod i tidsintervallet [0, π/2] underlager intervallet i 12 delar.

Ta 0 som ett första ögonblick, initial hastighet 0 och initial position 1.

Lösning

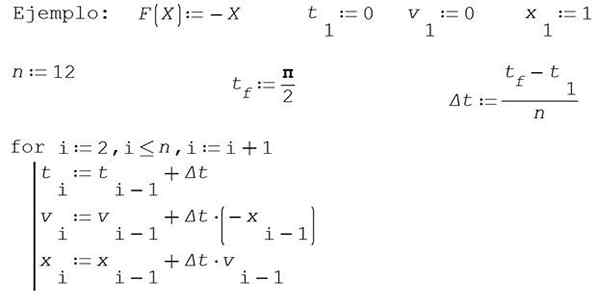
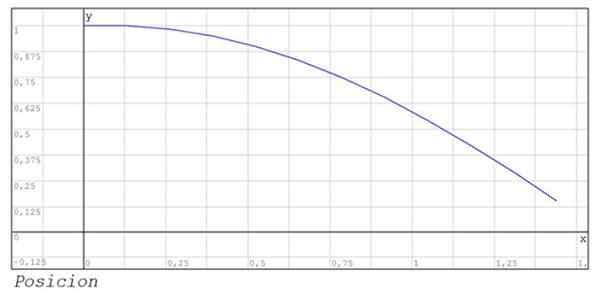
De numeriska resultaten visas i följande tabell:

Positionens grafik och hastigheten mellan instanserna 0 och 1 visas också.44.

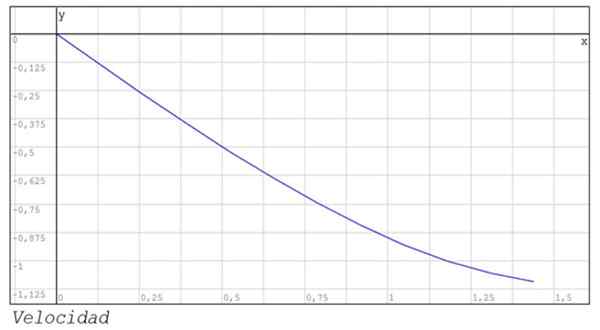
Föreslagna övningar för hemmet

Övning 1

Använd ett kalkylblad för att bestämma en ungefärlig lösning med Euler -metoden för differentiell ekvation:

och '= -exp (-y) med de initiala förhållandena x = 0, y = -1 i intervallet x = [0, 1]

Börja med ett steg på 0,1. Grafera resultatet.

Övning 2

Genom att använda ett kalkylblad, hitta numeriska lösningar på följande andra graders ekvation, var och det är en funktion av den oberoende variabeln T.

och "= - 1/y² med det initiala tillståndet t = 0; y (0) = 0,5; och '(0) = 0

Hitta lösningen i intervallet [0,5; 1.0] med ett steg på 0,05.

Grafera resultatet: och vs t; och 'vs t

Referenser

1. Eurlers metod.Hämtad från Wikipedia.org
2. Eulerlösare. Tagen från.Smut.com